Modern Maths for CAT 2026: PnC, Probability, Sets Strategy, Weightage & Practice Guide

Why Modern Math is necessary for CAT

Modern maths is necessary for CAT 2026 although the topics under modern maths are not high-priority topics, as you can find 1 - 2 questions from it. These concepts form more complex problems in integration with the other topics like Arithmetic, Algebra, Number system, and Geometry. So, it becomes necessary to learn CAT modern maths.

For example:

To find the number of diagonals in regular polygon of n – sides, we use the concept of combination.

Number of diagonals in n-sided polygon = $^nC_2-n$

Weightage of Modern maths in CAT over the years:

It is important to understand the CAT Quantitative Aptitude weightage of each topic in past 4 to 5 years of the CAT exam to kick start our preparation for CAT.

How Modern Maths Helps in Maximising CAT 2026 Score?

Questions from modern maths do not appear in bulk but still preparing it for CAT will give an edge. Advantages of preparing modern maths can be understood by following points:

• The questions form modern maths topics like permutation and combination, are often formula based and direct.

• Questions are conceptual but simple.

• Modern topics like sets and probability are useful for LR DI questions. You can find use of Venn diagrams while solving the questions of Data Interpretation.

• Preparing modern maths can give you an advantage because most of the aspirants focus on high priority topics like algebra and arithmetic. So, preparing modern maths along with these topics give you an edge.

• CAT Modern maths questions boost your accuracy.

Is Modern Maths Questions Related to Arithmetic/Algebra

Modern Mathematics is not an isolated or entirely new area in CAT preparation. In fact, it is an application and extension of core concepts from Arithmetic and Algebra, presented through a different logical framework. Topics such as Set Theory, Permutation & Combination, and Probability rely heavily on counting, ratios, equations, and algebraic manipulation. Understanding this interlinking helps you approach modern maths questions more confidently instead of treating them as unfamiliar problems.

Set Theory & Venn Diagrams

Set Theory is essentially about systematic counting and logical grouping of elements. When values are represented using Venn diagrams, the objective is to correctly count overlapping and non-overlapping regions to arrive at the desired answer.

• The process of assigning variables to different regions and forming equations is a direct application of Algebra.

• Concepts such as percentages, ratios, and averages, all core Arithmetic topics, are frequently used when values are given in percentage form.

• Many CAT questions can be solved by converting the visual Venn diagram into linear equations and simplifying them algebraically.

Thus, Set Theory acts as a bridge where Arithmetic data is structured through Algebraic logic.

Permutation & Combination (PnC)

Permutation and Combination is fundamentally based on counting, which makes it an extension of Arithmetic rather than a completely new concept.

• The Principle of Addition and Principle of Multiplication, which you already use in Arithmetic word problems, form the backbone of PnC.

• Factorials, simplifications, and expressions like nCr and nPr require strong Algebraic manipulation skills.

• Binomial expressions and identity-based simplifications further reinforce the algebraic nature of PnC.

If you understand Arithmetic counting logic and are comfortable with Algebraic simplification, PnC becomes far less intimidating.

Probability

Probability questions are essentially about comparing favourable outcomes with total possible outcomes.

• This comparison is nothing but a ratio, a core Arithmetic concept.

• Finding total outcomes often involves PnC-based counting, while simplifying probabilities involves basic Algebra.

• Advanced probability questions combine multiple areas, sets, counting methods, and conditional logic, yet the foundation remains Arithmetic ratios expressed algebraically.

$\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total Outcomes}}$

Concept 1: Permutation and Combination

The most fundamental application of mathematics is counting. There are many natural methods used for counting. In this section, we are dealing with various known techniques those are much faster than the usual counting methods and useful for CAT questions.

What is n! (n factorial)?

$n! =n \times (n-1) \times (n-2) ..... 3 \times 2 \times 1$

Example:

$5! =5 \times 4 \times 3 \times 2 \times 1=120$

Also, learn

Fundamental principle of Counting:

The fundamental principle of counting is used to determine the total number of possible outcomes in a situation out of multiple independent events.

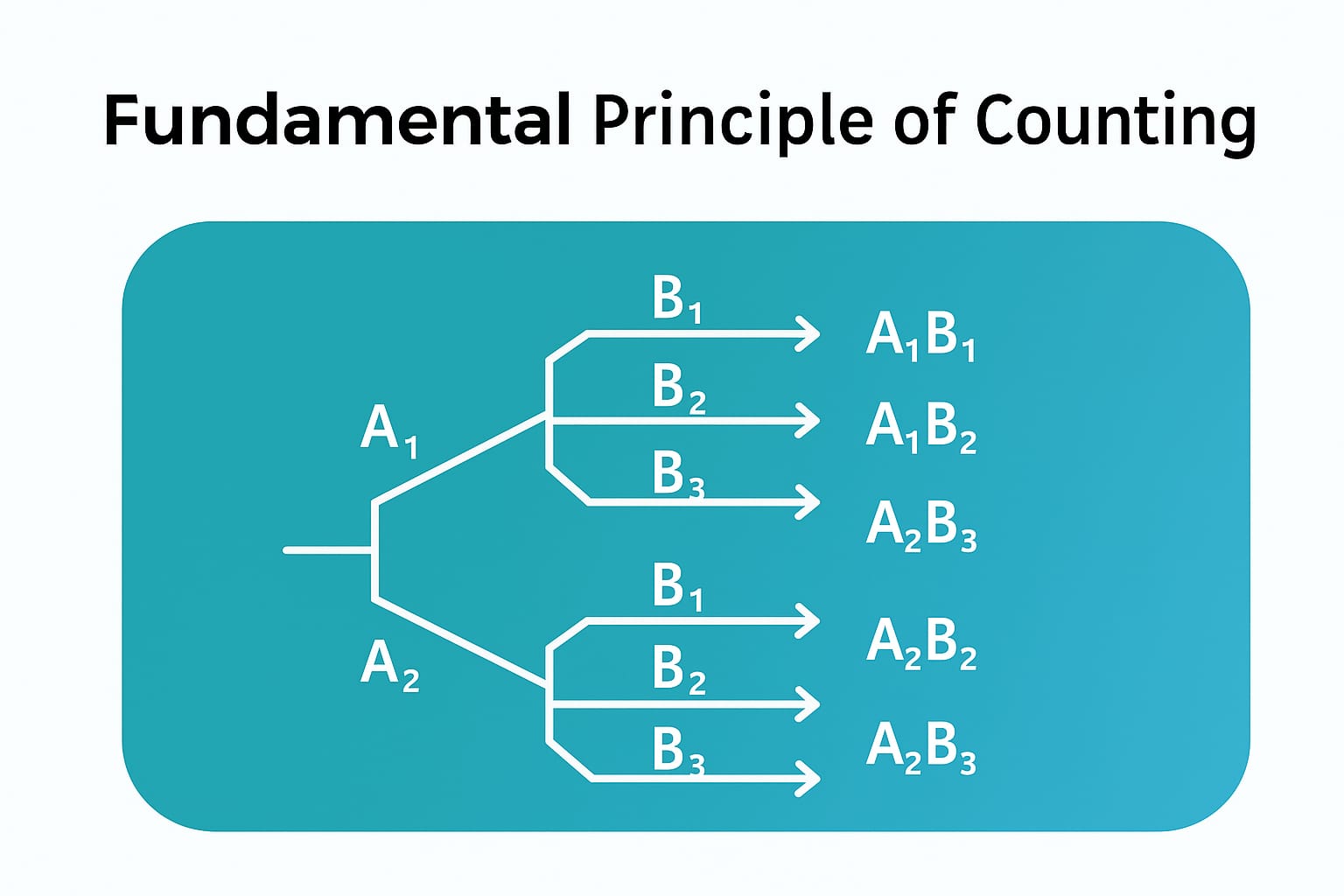
Let us understand this with a simple example:

Suppose you have two shirts ($A_1, A_2$) and three pairs of trousers ($B_1, B_2, B_3$), the question is in how many ways, you can dress yourself?

In this case, you are required to choose 1 shirt and 1 pair of trousers (Both are required). So, the possible combinations are $A_1B_1, A_1B_2, A_1B_3, A_2B_1, A_2B_2, A_2B_3$.

This is the fundamental principle of multiplication.

The formula: If you want to select 1 from n and 1 from m, then total number of combinations = $^nC_1 \times ^mC_1 = n \times m$

Suppose you have two pairs of shoes ($A_1, A_2$) and three pairs of slippers ($B_1, B_2, B_3$), the question is in how many ways, you can wear your footwear?

In this case, you are required to choose either 1 pair of shoes or 1 pair of slippers. So, the possible selections are $A_1, A_2, B_1, B_2, B_3$.

This is the fundamental principle of addition.

The formula: If you want to select 1 from n or 1 from m, then total number of selections = $^nC_1 + ^mC_1=n +m$

Permutations and Combinations:

How can we differentiate between Permutation and Combinations?

Combinations are used when we want to select r objects from n objects. (Selection only)

Total number of combinations = $^nC_r= \frac{n!}{(n-r)!r!}$

Permutations are used when we want to arrange r objects from n objects at r places. (Selection + Arrangement)

Total number of permutations = $^nP_r= \frac{n!}{(n-r)!}$

The Important Formulas and Concepts of Permutations and Combinations:

Permutations and Combinations Practice Questions for CAT:

Question 1: How many numbers between 10 and 10,000 can be formed by using the digits 1, 2, 3, 4, 5 if

(i) No digit is repeated in any number.

(ii) Digits can be repeated.

Solution: (i) Number of two-digit numbers = 5 × 4 = 20

Number of three-digit numbers = 5 × 4 × 3 = 60

Number of four-digit numbers = 5 × 4 × 3 × 2 = 120

Total = 200

(ii) Number of two-digit numbers = 5 × 5 = 25

Number of three-digit numbers = 5 × 5 × 5 = 125

Number of four-digit numbers = 5 × 5 × 5 × 5 = 625

Total = 775

Question 2: How many three-digit numbers can be formed using the digits 1, 2, 3, 4, 5, without repetition of digits?

How many of these are even?

Solution: Three places are to be filled with 5 different objects.

Number of ways = $^5P_3 = 5 × 4 × 3 = 60$

For the 2nd part, unit digit can be filled in two ways & the remaining two digits can be filled

in $^4P_2=12$ ways.

Number of even numbers = 2 × 12 = 24.

Question 3: There are fifteen players for a cricket match.

(i) In how many ways the 11 players can be selected?

(ii) In how many ways the 11 players can be selected including a particular player?

(iii) In how many ways the 11 players can be selected excluding two particular players?

Solution: (i) 11 players are to be selected from 15

Number of ways = $^15C_11 = 1365$.

(ii) Since one player is already included, we have to select 10 from the remaining 14

Number of ways = $^14C_10 = 1001$.

(iii) Since two players are to be excluded, we have to select 11 from the remaining 13.

Number of ways = $^13C_11 = 78$.

Concept 2: Selection & Grouping in Probability

Probability in CAT constitutes the questions based on basic formula, binomial, and conditional probability. These questions use the concept of election and grouping.

The basic formula:

$\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total Outcomes}}$

Probability is the logic of uncertainty and randomness. Uncertainty in an event and randomness of an event is a part our daily life. So, it becomes more interesting to understand probability.

How grouping, selection, and distribution link to probability?

Grouping, selection, and distribution are integrated part of probability as to describe the likely events or outcomes within a group, we use concept of selection and grouping (Combinations).

Since, probability is given by

$\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total Outcomes}}$

Total outcomes is a defined set, which we calculate using the concept of combinations

[Selecting r from n]. Probability determines the chance of a specific selection.

Important Formulas and Concepts on Probability:

1. Random Experiment

If all the possible outcomes of an experiment are known but the exact output cannot be predicted in advance, that experiment is called a random experiment.

Examples

(i) Tossing of a fair coin

When we toss a coin, the outcome will be either Head (H) or Tail (T)

(ii) Throwing an unbiased die

Die is a small cube used in games. It has six faces and each of the six faces shows a different number of dots from 1 to 6. Plural of die is dice.

When a die is thrown or rolled, the outcome is the number that appears on its upper face and it is a random integer from one to six, each value being equally likely.

(iii) Drawing a card from a pack of shuffled cards

A pack or deck of playing cards has 52 cards which are divided into four categories as given below

a. Spades (♠) [Black: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]

b. Clubs (♣) [Black: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]

c. Hearts (♥) [Red: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]

d. Diamonds (♦) [Red: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]

• Kings, Queens and Jacks are called face cards

2. Sample Space

Sample Space is the set of all possible outcomes of an experiment. It is denoted by S.

Examples

(i) When a coin is tossed, S = {H, T} where H = Head and T = Tail

(ii) When a dice is thrown, S = {1, 2 , 3, 4, 5, 6}

(iii) When two coins are tossed, S = {HH, HT, TH, TT} where H = Head and T = Tail

3. Event

Any subset of a Sample Space is an event. Events are generally denoted by capital letters A, B, C, D etc.

Examples

(i) When a coin is tossed, outcome of getting head or tail is an event

(ii) When a die is rolled, outcome of getting 1 or 2 or 3 or 4 or 5 or 6 is an event

4. Equally Likely Events

Events are said to be equally likely if there is no preference for a particular event over the other.

Examples

(i) When a coin is tossed, Head (H) or Tail is equally likely to occur.

(ii) When a dice is thrown, all the six faces (1, 2, 3, 4, 5, 6) are equally likely to occur.

5. Mutually Exclusive Events

Two or more than two events are said to be mutually exclusive if the occurrence of one of the events excludes the occurrence of the other.

This can be better illustrated with the following examples

(i) When a coin is tossed, we get either Head or Tail. Head and Tail cannot come simultaneously. Hence occurrence of Head and Tail are mutually exclusive events.

(ii) When a die is rolled, we get 1 or 2 or 3 or 4 or 5 or 6. All these faces cannot come simultaneously. Hence occurrences of

6. Independent Events

Events can be said to be independent if the occurrence or non-occurrence of one event does

not influence the occurrence or non-occurrence of the other.

Example: When a coin is tossed twice, the event of getting Tail(T) in the first toss and the event of getting Tail(T) in the second toss are independent events. This is because the occurrence of getting Tail(T) in any toss does not influence the occurrence of getting Tail(T) in the other toss.

7. Exhaustive Events

Exhaustive Event is the total number of all possible outcomes of an experiment.

Examples:

(i) When a coin is tossed, we get either Head or Tail. Hence there are 2 exhaustive events.

(ii) When two coins are tossed, the possible outcomes are (H, H), (H, T), (T, H), (T, T). Hence there are 4 (= 22) exhaustive events.

(iii) When a dice is thrown, we get 1 or 2 or 3 or 4 or 5 or 6. Hence there are 6 exhaustive events.

8. Algebra of Events

Let A and B are two events with sample space S. Then

(i) A ∪ B is the event that either A or B or Both occur. (i.e., at least one of A or B occurs)

(ii) A ∩ B is the event that both A and B occur

(iii) is the event that A does not occur

(iv) is the event that none of A and B occurs

Example: Consider a die is thrown, A be the event of getting 2 or 4 or 6 and B be the event of getting 4 or 5 or 6. Then

A = {2, 4, 6} and B = {4, 5, 6}

A ∪ B = {2, 4, 5, 6}

A ∩ B = {4, 6}

Probability Practice Questions for CAT:

Here we are going to discuss some CAT Quantitative Aptitude practice questions in Modern maths:

Question 1: A die is rolled once. Find the probability of

(i) getting a 3

(ii) getting a prime number

(iii) getting a 7

Solution:

(i) There are six possible ways in which a die can fall, out of these only one is favourable to the event.

P(3) = $\frac 16$

(ii) There are six possible ways in which a die can fall, out of these only 2, 3, and 5 are prime numbers.

P(3) = $\frac 36 = \frac 12$

(iii) 7 will never occur.

P(7) = $0$

Question 2: A card is drawn at random from a well shuffled deck of 52 cards. If A is the

event of getting a queen and B is the event of getting a card bearing a number greater than 4 but

less than 10, find P(A) and P (B).

Solution: Total number of possible outcomes is 52.

(i) There are 4 queens in a pack of cards.

P(A) = $\frac {4}{52} = \frac {1}{13}$

(ii) The cards bearing a number greater than 4 but less than 10 are 5,6, 7,8 and 9.

Each card bearing any of the above number is of 4 suits diamond, spade, club or heart.

Thus, the number of favourable outcomes = 5 × 4 = 20

P(B) = $\frac {20}{52} = \frac {5}{13}$

Question 3: From a bag containing 10 red, 4 blue and 6 black balls, a ball is drawn at

random. What is the probability of drawing

(i) a red ball? (ii) a blue ball? (iii) not a black ball?

Solution: (i) P(red) = $\frac {10}{20} = \frac 12$

(ii) P(blue) = $\frac {4}{20} = \frac 15$

(iii) P(not black) = $\frac {14}{20} = \frac 7{10}$

Concept 3: Sets and Venn diagram

In CAT, direct questions are not generally asked from Sets but this topic has importance in the questions of percentage, data interpretation, function, and other related topics.

In this section, we are going to discuss some important concepts related to set.

A set is a well-defined collection of elements. By well-defined elements it means that given a set and an element, it must be possible to decide whether or not the element belongs to the set.

How the sets are represented?

Sets are represented in two ways:

1. Roaster Form:

A set is described by listing elements, separated by commas, within brackets.

For example: Set of all prime numbers less than 20

A = {2, 3, 5, 7, 11, 13, 17, 19}

2. Set Builder Form:

A set can also be described by a characterizing property of the elements in the set.

For example: Set of all prime numbers less than 20

A = {x: x is a prime number less than 20}

Important concepts regarding sets:

Subset:

If every element of A is contained in B, then A is called the subset of B.

If A is subset of B, we write A ⊂ B, which is read as "A is a subset of B".

Null set:

Null set contains no elements, represented by ø or { }.

Power Set:

The set of subsets of a set is the power set of the set. If A is a set, then its Power set is denoted as P(A).

If A = {a, b, c}, then P(A) = {φ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}

Universal Set:

In any discussion in theory, there happens to be a set U that contains all sets under consideration. Such a set is called the universal set.

For example, in plane geometry the set of all points in the plane is the universal set.

Operations on Sets:

Concept of Venn diagram

Sets can be represented with the help of pictorial diagram using Venn diagram. Circles are used to represent the sets; common part of two intersecting circles represents the common elements of two sets. We generally use a rectangle to represent the universal set.

Example:

1.

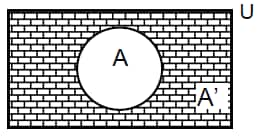
Shaded portion = A’ = compliment of A

2.

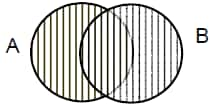
Shaded portion = A U B

3.

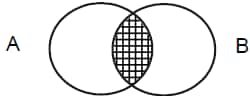
Shaded portion = A ∩ B

4.

AB

Shaded part = A – B

Sets and Venn diagram Practice Questions for CAT:

Question 1: In a certain city only two newspapers A & B are published. It is known that 25% of the city population reads A & 20% read B while 8% read both A & B. It is also known that 30% of those who read A but not B, look into advertisements and 40% of those who read B but not A, look into advertisements while 50% of those who read both A & B look into advertisements. What % of the population reads an advertisement?

Solution:

Let A & B denote sets of people who read paper A & paper B respectively and in all there are 100 people, then n(A) = 25, n(B) = 20, n (A ∩ B) = 8.

Hence the people who read paper A only i.e. n(A – B) = n (A) – n(A ∩ B) = 25 – 8 = 17.

And the people who read paper B only i.e. n(B – A) = n (B) – n (A ∩ B) = 20 – 8 = 12.

Now percentage of people reading an advertisement

= [(30% of 17) + (40% of + 12) + (50% of 8)]% = 13.9 %.

Question 2: In a prestigious business institute in north India, there are three specializations in business course and a student is can choose as many specializations as he wants. These specializations are Finance, Marketing and HRD. If 120 students specialize in Finance, 110 in Marketing and 125 are in HRD. 90 students have finance and Marketing both as their specialization, 85 have marketing and HRD while 80 have both finance and HRD. What can be the minimum and maximum number of students who can specialization in all the three fields?

Solution: Based on information given in the question, we can draw following Venn diagram

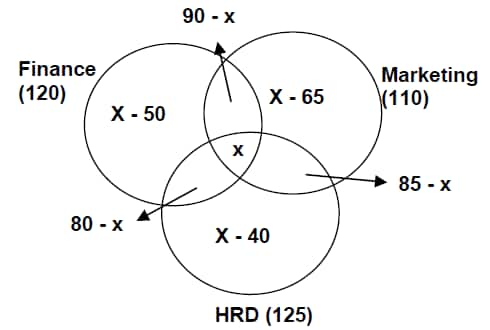
To find the minimum value of x, we have x – 65 ≥ 0 ⇒ x ≥ 65

And for maximum value of x, we have 80 – x ≥ 0 ⇒ x ≤ 80

Hence 65 ≤ x ≤ 80. So, we have the range of the values that can be the required solution.

How These 3 Concepts Cover All Modern Math Questions

Strategy to Master Modern Math for CAT

CAT Preparation Strategy involves continuous practice and revision of key concepts. Here’s a step-by-step strategy to master Modern Math for CAT covering topics like Permutations & Combinations, Probability, Set Theory, and Functions. You need to create a CAT preparation time table to prepare modern maths for CAT and then follow the given steps.

Step 1: Build strong foundation, conceptual knowledge of each topic.

Step 2: Focus on logic before formulae.

Step 3: Understand the interlinking of modern maths topics with the other section of Quantitative Aptitude like arithmetic, algebra etc.

Also, understand how the questions will form using the integration of these questions and practice accordingly.

Step 4: Prioritize high yield topics according to last 5 years trend.

Step 5: Solve NCERT questions to build concepts.

Step 6: Practice with previous year CAT questions.

Step 7: Practice mock tests and analyse them to manage your time, accuracy, and speed.

Common Pitfalls & How to Avoid Them

In this section we are dealing with the common mistakes, a student does often make while preparing for CAT and attempting questions during exam. Also, you should know how to tackle them.

Best CAT 2026 Resources to Ace Modern Maths

The best CAT 2026 resources for Modern Maths focus on building strong conceptual clarity along with consistent practice. A mix of standard textbooks, NCERT fundamentals, and reliable online learning platforms helps you understand topics like Set Theory, Permutation and Combination, and Probability in depth. Know about the best resources that aids your practice from the section below.

Top Books for Modern Maths CAT Prep

Online CAT 2026 Preparation Resources by Careers360

Online CAT 2026 preparation resources by Careers360 are designed to support structured and self-paced learning. You get access to expert-curated study material, topic-wise practice questions, mock tests, and performance analysis tools. These resources help you strengthen concepts, improve accuracy, and track progress efficiently throughout your CAT preparation journey.