The 10 Most Repeated Arithmetic Concepts in CAT (2020-2024)

Introduction to CAT Arithmetic Questions

The important arithmetic topics for CAT are as listed here

Why Arithmetic Questions Are Crucial in CAT

Arithmetic questions play a significant role in QA score in CAT. It becomes crucial because of the following reasons:

• Arithmetic has a healthy weightage in Quantitative Aptitude section every year. (Approximately 30% to 40%)

• In data interpretation also, the concepts of percentages, average, and ratios are widely used. Without a good understanding of these topics, you won’t be able to solve the questions of data interpretation.

• Arithmetic questions develop fundamental skills, conceptual understanding. Also, plays a significant role in overall score.

Weightage of Arithmetic in CAT Quant Section
As seen in previous years, here is a summary (year-wise and slot-wise) of the number of questions asked from Arithmetic in CAT

Data-Driven Insights: Easy vs. Moderate Questions

We have analysed the last 8 - 10 years' question papers. Before 2019, the level of questions in the quantitative aptitude section of CAT was generally moderate to hard.

But since the last 4 – 5 years, the level of questions in the quantitative aptitude section has ranged from easy to moderate. Out of 22 questions, you will find 6 – 8 questions which are not so tough to attempt. 8 – 10 questions are of a moderate level, and 3 – 4 questions can be moderate to hard.

How Repeated Arithmetic Topics Can Boost Your Score

Repeated concepts help students in several ways:

• After knowing about the concepts that are repeating, students can give a direction to their preparation.

• Students can develop strong fundamentals.

• Practising questions on repeated concepts increases accuracy and speed.

• Students became familiar with the question type and it will help in saving time during exams.

So, repeated arithmetic topics help students to boost their score.

1. Percentage and Profit-Loss

Percentages is one of the most important chapters in the syllabus of the CAT exam and the XAT examination. The importance of ‘percentages’ is supported by the fact that there are a lot of questions related to the use of percentages in all chapters, like Profit and Loss, Ratio and Proportion, Time and Work, Time, Speed and Distance, and Data interpretation.

Understanding the concepts of cost price (CP), selling price (SP), marked price (MP), Profit, Loss and discount is required to solve the questions based on profit and loss.

Repeated Question Types in CAT and PYQs

A few concepts from percentage, profit and loss are repeating consistently. Let’s have a look at these concepts:
Percentage (Repeated Concepts):

• Questions based on a Venn diagram

• Questions on successive change

• Income and expenses

• Percentages in average and mixtures

• Election-based questions

Q.1) In an election, there were four candidates, and 80% of the registered voters cast their votes. One of the candidates received 30% of the cast votes while the other three candidates received the remaining cast votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was

A) 50240

B) 40192

C) 60288

D) 60288

Solution:-

Let the number of voters be 300X

Then, votes cast = 240X

Number of votes received by the person who received 30% of the cast votes $\mathrm{=\frac{30}{100} \times 240 X=72 X}$

Remaining votes (240X – 72X) = 168X will be distributed as 28X, 56X, and 84X.

Given that, 84X – 72X = 2512

$\Rightarrow \mathrm{X=\frac{628}{3}}$

Thus, $\mathrm{300 X=300 \times \frac{628}{3}=62800}$

Hence, the correct answer is 62800.

Q.2) In a village, the ratio of number of males to females is 5 : 4. The ratio of number of literate males to literate females is 2 : 3. The ratio of the number of illiterate males to illiterate females is 4 : 3. If 3600 males in the village are literate, then the total number of females in the village is:

A) 43200

B) 42300

C) 43000

D) 43000

Solution:-

Let the number of males to females in the village be 5x and 4x, respectively.
Let the number of literate males to literate females in the village be 2y and 3y, respectively.
Let the number of illiterate males to illiterate females in the village be 4z and 3z, respectively.
$ \text { So, } \frac{2 y+4 z}{3 y+3 z}=\frac{5}{4}$
$ \Rightarrow 8 y+16 z=15 y+15 z $
$ \Rightarrow 7 y=z$
According to the question,
$⇒ 2y = 3600$
$\therefore y = 1800$
So, the total number of females in the village is:
3y + 3z = 3y + 21y = 24y = 24 × (1800) = 43200

Hence, the correct answer is option (1).

Q.3) A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes makes up $40 \%$ of his stock. That day, he sells half of the mangoes, 96 bananas and $40 \%$ of the apples. At the end of the day, he ends up selling $50 \%$ of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is

Solution:-

Let the initial number of fruits be $x$ and apples be $y$.

The stock of mangoes is given to be 40% of x, which shows that the number of mangoes will be $\frac{2x}{5}$.

The total number of sold fruits is given by including the selling of all the fruits- mango, apple and banana.

Now, the total no. of fruits sold

$=\frac{2x}{10}+\frac{4y}{10}+96=\frac{x}{2}$

$⇒\frac{x}{5}+\frac{2y}{5}+96=\frac{x}{2}$

On simplifying, we get,

$2x+4y+960=5x$

$⇒x=\frac{960+4y}{3}$

For $x$ to be a positive integer, let us check for values of $y$.

$4y+960$ has to be divisible by $3$, which means $4y$ will also be divisible by $3$.

For $\frac{4y}{10}$ to be an integer, $y$ has to be divisible by $5$.

We can say, that the smallest value of $y$ has to be a multiple of both $3$ and $5$, i.e. $15$.

Now, put the value of $y=15$.

We get, $x=\frac{960+4 \times 15}{3}$

$⇒x=\frac{1020}{3}$

$⇒x=340$

So, the smallest possible number of fruits in stock at the start of the day will be $340$.

Hence, the correct answer is $340$.

Q.4) In a group of 250 students, the percentage of girls was at least $44 \%$ and at most $60 \%$. The rest of the students were boys. Each student opted for either swimming or running or both. If $50 \%$ of the boys and $80 \%$ of the girls opted for swimming while $70 \%$ of the boys and $60 \%$ of the girls opted for running, then the minimum and maximum possible number of students who opted for both swimming and running are

A) 75 and 96, respectively

B) 72 and 88, respectively

C) 75 and 90 , respectively

D) 75 and 90 , respectively

Solution:-

We are given:
Total students = $250$
Minimum number of girls possible = 44% of 250 = 110, then boys = 140
Maximum number of girls possible = 60% of 250 = 150, then boys = 100

It is given that ; Among boys: $50\%$ swim, $70\%$ run
and among girls: $80\%$ swim, $60\%$ run

Let number of girls = $g$, then, boys = $b = 250 - g$

Now, total swimming strength = $0.5b + 0.8g$
total running strength = $0.7b + 0.6g$

Let the number of students who opted for both = $x$

Using the formula:

$\text{(Swim)} + \text{(Run)} - \text{(Both)} = 250$

So, $(0.5b + 0.8g) + (0.7b + 0.6g) - x = 250$

$⇒(1.2b + 1.4g) - x = 250 \Rightarrow x = 1.2b + 1.4g - 250$

Substitute $b = 250 - g$:
$x = 1.2(250 - g) + 1.4g - 250$
$⇒x = 300 - 1.2g + 1.4g - 250 = 50 + 0.2g$

Now check for minimum and maximum values of $x$ by plugging in $g = 110$ and $g = 150$:

• Minimum (at $g = 110$):

$x = 50 + 0.2 \times 110 = 50 + 22 = 72$

• Maximum (at $g = 150$):

$x = 50 + 0.2 \times 150 = 50 + 30 = 80$

Hence, the correct answer is option 4.

Profit and Loss (Repeated Concepts):

• Questions relating to CP, SP, and MP

• Calculating profit% using alligations

• Successive discounts

• Percentages in average and mixtures

Q.1) Ankita buys 4 kg cashews, 14 kg peanuts and 6 kg almonds when the cost of 7 kg cashews is the same as that of 30 kg peanuts or 9 kg almonds. She mixes all the three nuts and marks a price for the mixture in order to make a profit of Rs.1752. She sells 4 kg of the mixture at this marked price and the remaining at a 20% discount on the marked price, thus making a total profit of Rs. 744. Then the amount, in rupees, that she had spent in buying almonds is:

A) 1680

B) 1176

C) 2520

D) 2520

Solution:-

It is given,7C = 30P = 9A and Ankita bought 4C, 14P and 6A.
Let 7C = 30P = 9A = 630k
C = 90k, P = 21k, and A = 70k
Cost price of 4C, 14P and 6A = 4(90k)+14(21k)+6(70k) = 1074k
Marked up price = 1074k + 1752
$\begin{aligned} & \text { S.P }=\frac{1}{6}(1074 k+1752)+\left(\frac{4}{5}\right)\left(\frac{5}{6}\right)(1074 k+1752)=\frac{5}{6}(1074 k+1752) \\ & \text { S.P-C.P }=\text { profit } \\ & 1460-\frac{1074 k}{6}=744 \\ & \frac{1074 k}{6}=716\end{aligned}$
k = 4
Money spent on buying almonds = 420k = 420 × 4 = Rs 1680
The correct answer is Rs. 1680.

Q.2) The selling price of a product is fixed to ensure $40 \%$ profit. If the product had cost $40 \%$ less and had been sold for 5 rupees less, then the resulting profit would have been $50 \%$. The original selling price, in rupees, of the product is

A) 15

B) 20

C) 10

D) 10

Solution:-

Let the cost price be $x.$
Then selling price = $x + 40\% \text{ of } x = x + 0.4x = 1.4x$
Now, new cost price = $x - 40\% \text{ of } x = x - 0.4x = 0.6x$
New selling price = $1.4x - 5$

Given: profit in new case = $50\%$ of new cost price = $0.6x \times 0.5 = 0.3x$
So, New selling price = $0.6x + 0.3x=0.9x$
So, $1.4x - 5 = 0.9x$
$⇒1.4x - 0.9x = 5 \Rightarrow 0.5x = 5 \Rightarrow x = 10$
Original selling price = $1.4x = 1.4 \times 10 = 14$

Hence, the correct answer is option 4.

Q.3) Gopi marks a price on a product in order to make $20 \%$ profit. Ravi gets $10 \%$ discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is

A) 15

B) 25

C) 10

D) 10

Solution:-

Let the cost price of the product be $100x$.

Gopi wants to make a $20\%$ profit,
so the marked price (MP) is:

$
\text{MP} = 100x \times \left(1 + \frac{20}{100}\right) = 120x
$

Ravi gets $10$ % discount on the marked price, so the selling price (SP) is:

$
\text{SP} = 120x \times \left(1 - \frac{10}{100}\right) = 120 \times \frac{90}{100} = 108x
$

Now, the discount Ravi gets = $120x - 108x = 12x$

But the question says Ravi saves Rs 15,
So, $12x=15$

$⇒x=\frac{15}{12}=\frac54$

The profit made by Gopi = $108x - 100x = 8x= 10$ rupees.

Hence, the correct answer is option 3.

Shortcuts and Tricks for Quick Calculation

Speed and accuracy matter a lot while solving questions in the CAT exam. So, you should work on how to make quick calculations with accuracy.

Let’s discuss how you can improve your calculation speed:

• Learn Vedic maths for quick multiplication, addition, or subtractions.

• Learn tables up to 30.

• Learn squares up to 30.

• Learn cubes up to 30.

Apart from this, to find percentages quickly, you should learn conversion of percentage to fraction and vice versa.

Some important Tricks:

1. To find the net percentage change (In Successive Increase or Decrease), you can use the formula.
Net R% = $R_1 + R_2 + \frac{(R_1 \times R_2)}{100}$
2. If two articles were sold at equal price with a profit of a% on one article while loss of a% on the other. Then, there will always be a loss of $\frac {a^2}{100}$ %.
3. If n articles were purchased at equal price and sold at different prices. Then, net profit % is average of all profit %. Loss % will be treated as a negative of profit %.

2. Simple and Compound Interest

Principal: The original amount of money borrowed or invested.

Interest Rate: The interest charged on Rs 100 in one year.

Simple Interest:

Simple Interest (SI} is the interest earned or paid on the original principal during a specific period.

Compound Interest:

Definition: Compound Interest (Cl) refers to the interest that accumulates on both the initial principal and the accumulated interest from previous periods.

Most Common Formulas for CAT

List of CAT exam important formulas to solve the questions based on simple interest and compound interest:

Pattern of Past Questions

Previously, the questions were asked on the following concepts:

• Questions based on calculating simple interest

• Questions based on calculating compound interest

• The relation between simple interest and compound interest

• Loans and Installments

Q.1) Anil invests Rs 22000 for 6 years in a scheme with $4 \%$ interest per annum, compounded half-yearly. Separately, Sunil invests a certain amount in the same scheme for 5 years, and then reinvests the entire amount he receives at the end of 5 years, for one year at $10 \%$ simple interest. If the amounts received by both at the end of 6 years are equal, then the initial investment, in rupees, made by Sunil is

A) 20808

B) 20860

C) 20480

D) 20480

Solution:-

Anil’s investment:
Principal $ = \text{₹ }22000$
Rate per half year$ = 2\%$
Number of half years$ = 6 × 2 = 12$

So, amount = $22000 \times \left(1 + \frac{2}{100} \right)^{12} = 22000 \times \left(\frac{102}{100} \right)^{12}$

Now, Sunil invests ₹x for 5 years under same scheme:
Number of half years = 10

So, amount after 5 years = $x \times \left(\frac{102}{100} \right)^{10}$

This is reinvested at 10% simple interest for 1 year:

Amount = $x \times \left(\frac{102}{100} \right)^{10} \times \left(1 + \frac{10}{100} \right) = x \times \left(\frac{102}{100} \right)^{10} \times \frac{11}{10}$

Now equate this to Anil's amount:

$22000 \times \left(\frac{102}{100} \right)^{12} = x \times \left(\frac{102}{100} \right)^{10} \times \frac{11}{10}$

$⇒22000 \times \left(\frac{102}{100} \right)^2 = x \times \frac{11}{10}$

$⇒22000 \times \frac{10404}{10000} = x \times \frac{11}{10}$

$⇒20000 \times \frac{10404}{10000} = x $

$⇒x = 2 \times 10404 = 20808$

Hence, the correct answer is option 1.

Q.2) Alex invested his savings in two parts. The simple interest earned on the first part at 15% per annum for 4 years is the same as the simple interest earned on the second part at 12% per annum for 3 years. Then, the percentage of his savings invested in the first part is:

A) 37.5%

B) 62.5%

C) 60%

D) 65%

Solution:-

Let the investments of Alex be ‘a’ and ‘b’ in the two schemes.
So, interest earned on the first scheme = 0.15 × a × 4
Interest earned in the second scheme = 0.12 × b × 3

According to the question,
0.15 × a × 4 = 0.12 × b × 3
⇒ 20a = 12b
⇒ a : b = 3 : 5
$\therefore$ The percentage of Alex’s savings invested in the first scheme $=\frac{3}{3+5}×100=37.5\%$

Hence, the correct answer is 37.5%.

Q.3) Mr. Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is:

A) 20

B) 18

C) 16

D) 16

Solution:-

Let the total investment be 15x and the number of years required to be T years.

$
\begin{aligned}
& \frac{(3 \mathrm{x} \times 6 \times \mathrm{T})}{100}+\frac{(5 \mathrm{x} \times 10 \times \mathrm{T})}{100}+\frac{(7 \mathrm{x} \times 1 \times \mathrm{T})}{100} \geq 15 \mathrm{x} \\
&⇒ \frac{75 \mathrm{x} T}{100} \geq 15 \mathrm{x} \\
& ⇒ \mathrm{T} \geq 20
\end{aligned}
$
So minimum value of T is 20 years.

Hence, the correct answer is option (1).

3. Time, Speed, and Distance

Every year, 2 or 3 questions are asked from time, speed, and distance. You should understand the basic concept of time, speed, and distance.

Speed is the rate of covering of distance.

So, Speed = Distance/Time

Distance = Speed X Time

To convert kmph into m/s, multiply by 5/18.

To convert m/s into kmph, multiply by 18/5.

Important Formulas and Tricks

List of important formulas to solve the questions based on time, speed, and distance:

Previous years questions based on Time, speed, and distance

Q.1) Trains A and B start traveling at the same time towards each other with constant speeds from stations X and Y, respectively.
Train A reaches station Y in 10 minutes while train B takes 9 minutes to reach station X after meeting train A. Then the total time taken, in minutes, by train B to travel from station Y to station X is:

A) 6

B) 15

C) 10

D) 10

Solution:-

M – First meeting pointLet the speeds of trains A and B be ‘a’ and ‘b’, respectively.
$
\frac{x}{a}=\frac{D-x}{b}
$
It is given,
$
\begin{aligned}
& \frac{D}{a}=10 \text { and } \frac{x}{b}=9\\\
& \frac{x}{\frac{D}{10}}=\frac{D-x}{\frac{x}{9}}\ [\text{After putting the values}] \\
& ⇒\frac{10 x}{D}=\frac{9 D-9 x}{x} \\
&⇒ 10 x^2=9 D^2-9 D x \\
& ⇒10 \mathrm{x}^2+9 \mathrm{Dx}-9 \mathrm{D}^2=0
\end{aligned}
$
Solving, we get, $ x=\frac{3 D}{5}$
Solving, we get,
$
\frac{x}{b}=9
$
$\begin{aligned} &⇒ \frac{3 D}{b \times 5}=9 \\ & ⇒\frac{D}{b}=15\end{aligned}$

The total time taken by train B to travel from station Y to station X is 15 minutes.
Hence, the correct answer is option (2).

Q.2) Two ships meet mid-ocean, and then, one ship goes south and the other ship goes west, both traveling at constant speeds. Two hours later, they are 60 km apart. If the speed of one of the ships is 6 km per hour more than the other one, then the speed, in km per hour, of the slower ship is:

A) 20

B) 12

C) 18

D) 18

Solution:-

Let the speeds of two ships be x and (x + 6) km per hour.

Distance covered in 2 hours will be 2x and (2x + 12).

$
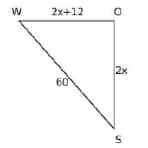
\begin{aligned}
& (2 x)^2+(2 x+12)^2=60^2 \\
& ⇒(x)^2+(x+6)^2=30^2 \\
& ⇒ 2 x^2+12 x+36=900 \\
& ⇒x^2+6 x+18=450 \\
& ⇒ x^2+6 x-432=0\\
& ⇒ (x+24)(x-18)=0
\end{aligned}
$
Solving, we get $\mathrm{x}=18$ or $x = -24$
As speed can't be negative, the speed of the slower ship is 18 km/hr.

Hence, the correct answer is option (3).

Q.3) A straight road connects points A and B. Car 1 travels from A to B and Car 2 travels from B to A, both leaving at the same time. After meeting each other, they take 45 minutes and 20 minutes, respectively, to complete their journeys. If Car 1 travels at the speed of 60 km/hr, then the speed of Car 2, in km/hr, is

A) 100

B) 90

C) 80

D) 80

Solution:-

Let the speed of Car 2 be ' $x$ ' kmph and the time taken by the two cars to meet be ' $t$ ' hours. In 't' hours, Car 1 travels $(60 \times t)$ km while Car 2 travels $(x \times t) \mathrm{km}$

It is given that the time taken by Car 1 to travel $(x \times t)$ km is 45 minutes or ($\frac34$) hours.

$\therefore \frac{(x \times t)}{60}=\frac{3}{4} ⇒ t=\frac{180}{4 x}$......(i)

Similarly, the time taken by Car 2 to travel $(60 \times t)$ is 20 minutes or $(\frac1 3)$ hours.

$\therefore \frac{(60 \times t)}{x}=\frac{1}{3}$ or

$\therefore t=\frac{x}{180}$ ....(ii)

Equating the values in (i) and (ii), and solving for x:

$\therefore \frac{180}{4 x}=\frac{x}{180} \Rightarrow x=90$ kmph

Hence, the correct answer is 90.

4. Time and Work

Total work refers to the complete task or job that needs to be accomplished. In questions related to time and work, it's crucial to understand the entire scope of the work because all further calculations, be it regarding time or the number of workers required, will revolve around this concept.

The concept of 1 day work refers to the portion of the total work that an individual or a machine completes in one day. It's an essential tool to compare efficiencies and to calculate combined work when multiple entities work together

Concept of Time and Work in Pipes & Cisterns

Definition: Pipe and cistern problems involve filling or emptying a tank or reservoir. The pipes can either fill (inlet pipes) or empty (outlet pipes) the tank. The 'Time and Work' principles can be directly applied to these problems with the 'work' being represented as the volume of the tank.

Note: Work of filling pipe is treated as positive while the work of emptying pipe/hole/drainage pipe/leak is treated as negative.

Important formulas related to Time and Work

PYQs & Frequently Repeated Patterns

Q.1) Renu would take 15 days working 4 hours per day to complete a certain task, whereas Seema would take 8 days working 5 hours per day to complete the same task. They decide to work together to complete this task. Seema agrees to work for double the number of hours per day as Renu, while Renu agrees to work for double the number of days as Seema. If Renu works 2 hours per day, then the number of days Seema will work is

Solution:-

Renu takes 15 days × 4 hours/day = 60 hours to complete the task.
So, Renu's efficiency = $\frac{1}{60}$ work per hour.

Seema takes 8 days × 5 hours/day = 40 hours to complete the task.
So, Seema's efficiency = $\frac{1}{40}$ work per hour.

Renu works 2 hours/day. Let Seema work for $x$ days.
Then, Renu works for $2x$ days and Seema works 4 hours/day (double of Renu).

Total work done by Renu = $2x \times 2 \times \frac{1}{60}$

$= \frac{4x}{60} = \frac{x}{15}$
Total work done by Seema = $x \times 4 \times \frac{1}{40}$

$= \frac{4x}{40} = \frac{x}{10}$

Total work = $\frac{x}{15} + \frac{x}{10} = 1$
$\Rightarrow \frac{2x + 3x}{30} = 1 \Rightarrow \frac{5x}{30} = 1$
$\Rightarrow x = 6$

Hence, the correct answer is $6$.

Q.2) Working alone, the times taken by Anu, Tanu, and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job that they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is:

A) 6

B) 8

C) 4

D) 4

Solution:-

Let the time taken by Anu, Tanu, and Manu be 5x, 8x, and 10x hours.
$\therefore$ Total work = LCM of (5x, 8x, and 10x) = 40x
Anu can complete 8 units in one hour.
Tanu can complete 5 units in one hour.
Manu can complete 4 units in one hour.
It is given that, three of them together can complete the work in 32 hours.
$32(8+5+4)=40x$
$\therefore x=\frac{68}{5}$
It is given,
Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day, i.e. 36 + 4 = 40 hours
$\begin{aligned} & 40(8+5)+y(4)=40 x \\ &⇒ 4 y=24 \\ & \therefore y=6\end{aligned}$
Manu alone will complete the remaining work in 6 hours.

Hence, the correct answer is option (1).

Q.3) style="text-align:justify">John takes twice as much time as Jack to finish a job. Jack and Jim together take one-third of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than the three of them working together. In how many days will Jim finish the job working alone?

A) 4

B) 5

C) 6

D) 6

Solution:-

Given: John takes twice as much time as Jack to finish a job. Jack and Jim together take one-third of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than the three of them working together.
Let Jack take $x$ days to finish a job.
So, John will take $2x$ days to finish the job.
Also, Jack and Jim take $\frac{2x}{3}$ days to finish the job.
Now, let the total work be LCF ($x,2x,\frac{2x}{3}$) = $2x$ units
So, the efficiency of Jack = $\frac{2x}{x}$ = 2,
The efficiency of John = $\frac{2x}{2x}$ = 1,
The total efficiency of Jack and Jim = $\frac{2x}{\frac{2x}{3}}$ = 3
So, the efficiency of Jim = (2 – 1) = 1
According to the question,
To finish the job, John takes three days more than the three of them working together.
⇒ $2x=\frac{2x}{2+1+1}+3$
⇒ $8x=2x+12$
⇒ $x=2$
Therefore, working alone Jim will finish the job in $\frac{2×2}{1}$ = 4 days.
Hence, the correct answer is option (1).

Q.4) Pipes A and C are fill pipes while Pipe B is a drain pipe of a tank. Pipe B empties the full tank in one hour less than the time taken by Pipe A to fill the empty tank. When pipes A, B, and C are turned on together, the empty tank is filled in two hours. If pipes B and C are turned on together when the tank is empty and Pipe B is turned off after one hour, then Pipe C takes another one hour and 15 minutes to fill the remaining tank. If Pipe A can fill the empty tank in less than five hours, then the time taken, in minutes, by Pipe C to fill the empty tank is

A) 90

B) 60

C) 120

D) 120

Solution:-

If A takes x hours to fill the tank alone, then B needs (x-1) hours to empty the tank alone, and C needs y hours to fill the tank alone.
According to the question:
$\frac{1}{x}-\frac{1}{(x-1)} + \frac1y = \frac12$
So, $\frac1y =\frac12-\frac{1}{x}+\frac{1}{(x-1)}$
Pipe B and C worked together for 1 hour. Pipe C further worked for 1 hr and 15 minutes i.e. 1.25 hrs to finish the work.
So, $\frac{- 1}{(x-1)} + \frac1y + \frac{1.25}y = 1$
⇒ $- \frac1{(x-1)} + \frac{2.25}y = 1$
After solving both equations, we have x = 3 and y = $\frac32$ hrs = 90 minutes
Therefore, Pipe C takes 90 minutes to fill the empty tank.

Hence, the correct answer is option (1).

5. Ratio and Proportion

A ratio is a comparison between two quantities, showing the relative size of one quantity to another. It is often expressed in the form 'a:b', where "a" and "b" are the two quantities.

Proportion:

1. If two ratios a:b and c:d, are equal then they are said to be in equal proportion.

a/b = c/d

2. In the ratio a:b,

Proportion of a = a/(a+b)

Proportion of b = b/(a+b)

Key Concepts Frequently Tested

The following concepts are repeated asked in CAT exam

6. Mixtures and Alligations

Questions of mixture and alligation are solved by using either the method of allegation or weighted average.

Rule of Alligation

The Rule of Alligation is a method of finding the ratio in which two or more ingredients at given prices must be mixed to produce a mixture of a desired price. This rule is especially useful in solving problems related to mixtures.

Formula:

If two ingredients A and B are mixed in a ratio x : y respectively, then

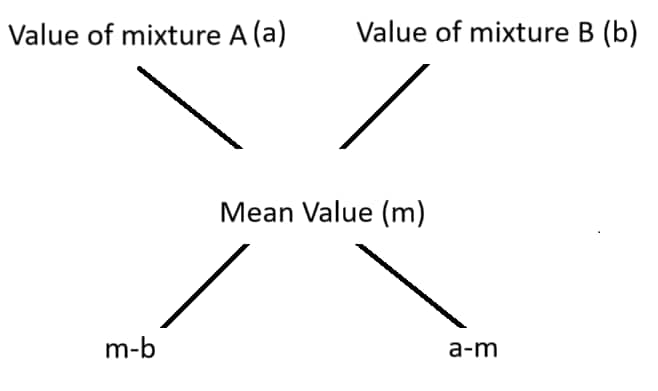
Then $\frac {x}{y} = \frac {(m-b)}{(a-m)}$

Shortcut for Quick Solving

1. Quantity of dearer/Quantity of Cheaper = [Mean price(m) - C.P. of cheaper(c)]/[C.P of Dearer (d) - Mean price (m) ]

2. If a Container contains ‘x’ units of pure liquid, and we replace the liquid with ‘y’ units of water:

Then after ‘n’ successive replacements, the units of pure liquid left is $x(1-\frac {y}{x})^n$

7. Averages

Definition: The average of a set of numbers is the sum of those numbers divided by the count of the numbers.

Mathematically:

Average = (Sum of all numbers)/(Count of all numbers)

Concept of Weighted Average:

Definition: The weighted average (or weighted mean) is an average in which each quantity in the dataset is assigned a weight. These weights determine the relative importance of each quantity on the average.

Mathematically:

Average = $\frac {(n_1 x_1+n_2 x_2+⋯)}{(n_1+n_2+⋯)}$

Where, x1, x2, x3, … are the averages of n1, n2, n3, … observations respectively.

Repeated Question Types in CAT and PYQs

Questions are repeatedly asked on mainly three concepts

• Calculation of ages

• Relating arithmetic mean and geometric mean

• Questions involving the concept of weighted average

Q.1) Let A, B, and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is

A) 5

B) 4

C) 6

D) 6

Solution:-

Given

$A + \frac{(B + C)}2 = 5 ⇒ 2A + B + C = 10$ ….(i)

$\frac{(A + C)}2 + B = 7 ⇒ A + 2B + C = 14$ …..(ii)

(i) – (ii) ⇒ B - A = 4 ⇒ B = 4 + A

Given that A, B, and C are positive integers

If A = 1 then B = 5 and C = 3

If A = 2, then B = 6 and C = 0, but this is invalid as C is positive.

Similarly, if A > 2, C will be negative, and the cases are not valid.

Hence, A + B = 6.

Hence, the correct answer is 6.

Q.2) The mean of all 4-digit even natural numbers of the form 'aabb', where a > 0, is

A) 4466

B) 5050

C) 4864

D) 4864

Solution:-

The four-digit even numbers will be of form:

$1100, 1122, 1144 ... 1188, 2200, 2222, 2244 ... 9900, 9922, 9944, 9966, 9988$

Their sum 'S' will be $(1100+1100+22+1100+44+1100+66+1100+88) + (2200+2200+22+2200+44+...) .... + (9900+9900+22+9900+44+9900+66+9900+88)$

⇒ $S = 1100×5 + (22+44+66+88) + 2200×5 + (22+44+66+88)....+ 9900×5 + (22+44+66+88)$

⇒ $S = 5×1100(1+2+3+...9) + 9(22+44+66+88)$

⇒ $S=5×1100×9×10/2 + 9×11×20$

The total number of numbers is 9 × 5 = 45

∴ Mean will be $S/45 = 5 × 1100 + 44 = 5544$.

Hence, the correct answer is 5544.

Q.3) Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to

A) 26

B) 20

C) 18

D) 18

Solution:-

Let the fixed monthly expenditure be $M$ rupees.

First three months: $10, 20, 25$ per kg. Amount spent $= M$ each month.

Quantity bought: $\frac{M}{10},\ \frac{M}{20},\ \frac{M}{25}$ kg respectively.

Next two months, expenditure $= \frac{M}{2}$ each month, prices $25, 50$ per kg.

Quantity bought: $ \frac{M/2}{25} = \frac{M}{50},\ \frac{M/2}{50} = \frac{M}{100}$ kg.

Total expense $ = 3M + \frac{M}{2} + \frac{M}{2} = 4M$

Total quantity $ = \frac{M}{10} + \frac{M}{20} + \frac{M}{25} + \frac{M}{50} + \frac{M}{100} $

$= \frac{10M + 5M + 4M + 2M + M}{100}$

$= \frac{22M}{100} = \frac{11M}{50} $

Average price per kg$= \frac{\text{Total expense}}{\text{Total quantity}} = \frac{4M}{11M/50} = \frac{200}{11} \approx 18.18=18$

Hence, the correct answer is option 3

Variations and Advanced Applications

• Average is an important concept which is used to solve the problems of weighted average, problems including ages, mixture and alligations etc.

• Averages are used in day-to-day life calculations.

• Used in making estimation

Important formulas and tricks

1. When a person replaces another person then average age of the group will be increased or decreased.

Difference between the persons added and who left = change in average x number of persons.

2. When a person joins the group of n persons; if average increases then

Age of new person = Old average + (n+1) $\times$ difference between averages

If average decreases then

Age of new person = Old average - (n+1) $\times$ difference between averages

3. Average of an AP of odd terms is always its middle term.

4. In general case, Average of an AP is Average of its first and last term.

5. Average of an AP of even terms is average of its two middle terms.

6. Arithmetic mean is always greater than or equal to geometric mean.

8. Questions on Integration of Ratio, Percentage, and Profit-Loss Combined

In CAT, questions on integration of ratio with percentages, integration of ratio with profit and loss are being repeatedly asked.

Questions type may be:

Ratio of population of male and female are given and then increased or decreased by some percentages, percentage change in total population may be asked. Such kind of questions can be framed.

Number of articles are given in the form of ratios, selling rate and purchase rate are given in another ratio, and you might be asked the net profit or loss percent. There can be other variations of questions.

PYQs

Q.1) A person buys tea of three different qualities at INR 800,INR 500, and INR 300 per kg, respectively, and the amounts bought are in the proportion 2 : 3 : 5. She mixes all the tea and sells one-sixth of the mixture at 700 per kg. The price, in INR per kg, at which she should sell the remaining tea, to make an overall profit of 50%, is:

A) 653

B) 688

C) 692

D) 692

Solution:-

Let the person bought 2x, 3x, and 5x kg of the three different qualities at INR ₹800, INR 500, and INR 300 per kg respectively. Let the selling price of the remaining tea be ‘P’.

$\begin{aligned} & (2 x \times 800+3 x \times 500+5 x \times 300)(1+50 \%)=\left(\frac{1}{6} \times 10 x \times 700\right)+\left(\frac{5}{6} \times 10 x \times P\right) \\ & 4600\left(\frac{3}{2}\right)=\frac{7000}{6}+\frac{50 P}{6} \text { or } \mathrm{P}=688\end{aligned}$
Hence, the correct answer is 688.

Q.2) The salaries of three friends Sita, Gita, and Mita are initially in the ratio 5:6:7, respectively. In the first year, they get salary hikes of 20%, 25%, and 20%, respectively. In the second year, Sita and Mita get salary hikes of 40% and 25%, respectively, and the salary of Gita becomes equal to the mean salary of the three friends. The salary hike of Gita in the second year is:

A) 26%

B) 28%

C) 25%

D) 25%

Solution:-

Let the initial salaries of Sita, Gita and Mita be 500, 600 and 700 respectively.
After getting 20%, 25% and 20% salary hikes respectively, their salaries become 600, 750 and 840 respectively.
In the second year, Sita and Mita get 40% and 25% hikes respectively.
So, after two years the salaries of Sita and Mita are 840 and 1050 respectively.
We also know that Gita’s salary is the average of the salaries of the three which is equal to the average of the other two i.e. $\frac{840+1050}{2} = 945$
So, the hike in the salary of Gita during the second year = $\frac{945-750}{750} \times 100 = 26$%
Hence, the correct answer is option (1).

9. Simple Equations in Arithmetic

Questions asked from percentages, profit and loss, and other arithmetic topics can be solved by forming linear equations.

Linear Equations for Word Problems

Word problems on ages are generally solved forming simple linear equations. We can understand this by taking a simple example:

“7 years ago, P was half as old as Q. After 5 years, their total age will be 48. Find their present ages.”

Let present age of P = P, Q = Q.

Equation 1: 2(P – 7) = Q - 7

Equation 2: (P + 7) + (Q + 7) = 48, solve these two equations to get the value of P and Q.

In Profit and Loss:

“A bought 10 pencils for Rs. 80 and sold them at Rs. x each. Find x if his profit % is 20.”

Total selling price = 120% of total cost price = 10x
Solve this equation to get the value of x.

Similarly, we can solve the questions on mixture and allegation, time and work, TSD, etc by forming simple equations.

Previously asked questions

Q.1) A gentleman decided to treat a few children in the following manner: He gives half of his total stock of toffees and one extra to the first child, then the half of the remaining stock along with one extra to the second, and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were in his stock initially?

A) 62

B) 60

C) 50

D) 50

Solution:-

Let the initial number of chocolates be $64x$.
The first child gets $(32x + 1)$ and $(32x - 1)$ are left.
2nd child gets $(16x + \frac{1}{2})$ and $(16x - \frac{3}{2})$ are left
3rd child gets $(8x + \frac{1}{4})$ and $(8x - \frac{7}{4})$ are left
4th child gets $(4x + \frac{1}{8})$ and $(4x - \frac{15}{8})$ are left
5th child gets $(2x + \frac{1}{16} )$ and $(2x - \frac{31}{16})$ are left.
Given, $2x - \frac{31}{16} = 0 ⇒ 2x=\frac{31}{16} ⇒ x=\frac{31}{32}$.
So, initially, the Gentleman has $64x$ i.e. $64 × \frac{31}{32} =62$ chocolates.
Hence, the correct answer is option (1).

Q.2) Amal purchases some pens at INR 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at INR 12 each. If the remaining pens are sold at INR 11 each, then he makes a net profit of INR 300, while he makes a net loss of INR 300 if the remaining pens are sold at INR 9 each. The wage of the employee, in INR, is:

A) 1000

B) 800

C) 1500

D) 1500

Solution:-

Let the number of pens purchased be n.
Then the cost price is 8n.
The total expenses incurred would be 8n + W, where W refers to the wage of the employee
Then selling price in the first case = 12 × 100 + 11 × (n – 100)
Given profit is 300 in this case.
So, 1200 + 11n – 1100 – 8n – W = 300
⇒ 3n – W = 200---------(1)
In the second case: 1200 + 9n – 900 – 8n – W = –300 (Loss)
⇒ W – n = 600-----------(2)
Adding equation 2 and equation 1, we get,
2n = 800
$\therefore$ n = 400
So, W = 600 + 400 = 1000

Hence, the correct answer is 1000.

Q.3) The price of a precious stone is directly proportional to the square of its weight. Sita has a precious stone weighing 18 units. If she breaks it into four pieces with each piece having a distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000. Then, the price of the original precious stone is

A) 1296000

B) 1944000

C) 972000

D) 972000

Solution:-

If W is the weight of the stone and P is the price of that stone, then P = k × W2
Price of unbroken stone = 182 × k = 324 k.
Total cost is minimum if the weight of broken stones are close to each other, that is, the weights are 3, 4, 5, and 6 units.
Total cost in this case = k(32+42+52+62) = 86k
Total cost is maximum when the weights of the broken stones are far from each other, that is, the weights are 1, 2, 3, and 12 units.
Total cost in this case = (12+22+32+122)k = 158k
According to the question
158k – 86k = 72k = 2,88,000
⇒ k = 4,000
So, the price of the unbroken stone = 182k = 324k = 12,96,000

Hence, the correct answer is option (1).

10. Problems using ratio, average, time & work, and TSD

In CAT, TSD, time and work make good questions with averages and ratios. Questions on these concepts are frequently asked.

Most Asked Concepts in Past CAT Papers

1. Ratio with time, speed and distance:
Important concept:
Speed is directly proportional to Distance
$\frac {S_1}{S_2} = \frac {D_1}{D_2}$
Speed is inversely proportional to time
$\frac {S_1}{S_2} = \frac {T_2}{T_1}$

2. Average with speed, distance, and time:
Key concept: Average speed = Total distance covered/Total time taken

3. Ratio with time and Work:
Key concept: Time is inversely proportional to efficiency

Practice Questions from 2020–2024 Question Paper

Q.1) A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at a 20% profit and the laptop at a 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is:

A) 20000

B) 18000

C) 16000

D) 16000

Solution:-

Using the Alligation Rule, the ratio of cost prices of desktop and laptop will be:

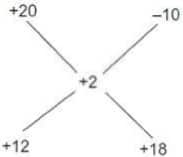
i.e., 12:18 = 2:3

∴ The cost of desktop = $\frac25$ × 50000 = Rs. 20000

Hence, the correct answer is option (1).

Q.2) A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other. Ram and Rahim reach their destination in one minute and four minutes, respectively. if they start at the same time, then the ratio of Ram's speed to Rahim's speed is

A) $\frac{1}{2}$

B) $\sqrt2$

C) 2

D) 2

Solution:-

The required ratio of speeds = Square root of the inverse ratio of times taken after crossing each other

$\mathrm{=\sqrt{4}: \sqrt{1} \: i.e., 2: 1}$
hence, the correct answer is 2 : 1.

Q.3) The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is:

A) 3 : 2

B) 11 : 7

C) 11 : 3

D) 11 : 3

Solution:-

Let Neeta, Geeta, and Sita earn N, G, and S amounts per day.

Given that,
N + G = 6S ……(1)
S + N = 2G …….(2)

Substituting (2) in (1) for N,
2G – S + G = 6S
⇒ 3G = 7S
⇒ $\frac{\text{G}}{\text{S}}=\frac{7}{3}$

Substituting (2) in (1) for S,
N + G = 6(2G – N)
⇒ 7N = 11G
⇒ $\frac{\text{N}}{\text{G}}=\frac{11}{7}$

$\therefore$ N : G : S = 11 : 7 : 3

Hence, the correct answer is 11 : 3.

Q.4) Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is

Solution:-

Let Amar, Akbar, Anthony's 1 month work be $a,\ b,\ c$ respectively.

$a+b = \frac{1}{12},\quad b+c = \frac{1}{16},\quad c+a = \frac{1}{24}$

Adding all: $2(a+b+c) = \frac{1}{12} + \frac{1}{16} + \frac{1}{24}$

$2(a+b+c) = \frac{4+3+2}{48} = \frac{9}{48} = \frac{3}{16}$

$a+b+c = \frac{3}{32}$

$a = \frac{3}{32} - \frac{1}{16} = \frac{1}{32}$

$b = \frac{1}{12} - \frac{1}{32} = \frac{8-3}{96} = \frac{5}{96}$

$c = \frac{1}{16} - \frac{5}{96} = \frac{6-5}{96} = \frac{1}{96}$

Speeds: $a=\frac{1}{32},\ b=\frac{5}{96},\ c=\frac{1}{96}$

Order of speed: fastest $b$, slowest $c$, middle $a$.

Time taken by Amar alone $ = \frac{1}{a} = 32$ months

Preparation Tips for CAT Arithmetic

To prepare CAT arithmetic section, here is a structured approach that will help you boost your CAT percentile.

Common mistakes in arithmetic and their remedies

There are many common mistakes made by a student during preparation and appearing for the CAT exam.

How to Improve Accuracy and Speed

To improve accuracy and speed,

• Learn Vedic maths for the CAT exam for multiplication and finding the square of larger numbers.

• Learn percentage to fraction conversion and vice versa.

• Learn squares, cubes, and tables up to 30.

• Practice questions daily on each topic according to the plan made by you. Also, practice PYQs.

• Do mental maths.

Time Management for Quant Section

During the exam, you should do:

• Allocate time to each question separately.

• Do not waste much time on one question.

• Avoid lengthy calculations.

• Avoid the use of pen when the calculations can be done mentally.

• Always check on time shown on your screen.

Mock Test & Revision Strategy

Practice sets on arithmetic play an important role in boosting your CAT percentile.

What you should do:

• Attempt at least one small practice set in a day.

• Identify the areas where you are making mistakes most and work on them to rectify.

• Make a record of the time taken by you in every test and the score of each test.

• Identify the question patterns you are taking more time on and try to reduce the time in the next test.

• Check if your score improves after the test. In these ways, you can track your performance.

These practices will certainly help you to improve.

Best resources & practice material for CAT Algebra

1. Arun Sharma: A Quantitative Approach for CAT (7th Edition)
2. Quantitative Aptitude for CAT by Nishit K Sinha

CAT 2025 Preparation Resources by Careers360

The candidates can download the various CAT preparation resources designed by Careers360 using the links given below.