ITM Business School MBA Admissions 2026
400+ Company Visits | Highest CTC Offered: 21 LPA | Average CTC Offered: 8.65 LPA | 100% Placement Assurance
Search Colleges, Exams, Schools & more
Login
CAT Quant Formula List 2025: Important Formulas, Shortcuts & Last-Minute Revision Guide
As CAT 2025 approaches, with the exam scheduled on November 30, 2025, revising all key CAT Quant formulas becomes essential for boosting speed and accuracy in the QA and DI sections. Even well-prepared candidates lose marks due to last-minute confusion in basic and advanced formulas. This guide compiles all topic-wise CAT Quant formulas-Arithmetic, Algebra, Geometry, Mensuration, Time & Work, TSD, and more-to help you strengthen your revision and improve your overall CAT 2025 score.
This Story also Contains
- CAT Arithmetic Important Formulas
- CAT Algebra Formulas
- CAT Geometry and Mensuration Formulas
- CAT Important Formulas of Trigonometry
- CAT Permutation& Combination and Probability Key Formulas
- CAT 2025 Formula Sheet: Why You Need It?
- CAT 2025 Recommended eBooks and Study Materials
CAT Arithmetic Important Formulas
The Arithmetic section is the most important section in the Quantitative Aptitude Section, which is also useful to solve the Data Interpretation problems. The following are some 50+ Important Formulas for CAT Preparation of this section, which are given in this CAT Formula Sheet:
Percentage:
Following are some basic and Important Formulas for CAT 2025 related to percentages:
|
Concept |
Formula |
|
To compare two numbers in terms of percentage |
$X \text{ is what percentage of } Y = \frac{X}{Y} \times 100$ $X \text{ is what percentage more/less than } Y = \frac{|X - Y|}{Y} \times 100$ |
|
To find the percentage |
$X \text{ % of } Y = \frac{XY}{100}$ |
|
Successive Change (If a value is changed successively by $R_1$ and $R_2$%) |
Net %change = $R_1 + R_2 + \frac {R_1R_2}{100}$% Where $R_1$ and $R_2$ are taken as positive for increase and negative for decrease. |
Profit & Loss:
Following are some basic and Important Formulas for CAT 2025 related to Profit and Loss:
|
Concept |
Formula |
|
Relating Selling Price (SP), Cost Price (CP), and Profit |
$S.P. = C.P. + \text{Profit}$ |
|
Relating Selling Price (SP), Cost Price (CP), and Loss |
$S.P. = C.P. - \text{Loss}$ |
|
To find Profit or Loss Percentage |
Profit/Loss % = $\frac {\text{Profit or Loss}}{CP} \times 100$% |
|
To find discount Percentage |
Discount % = $\frac {\text{Discount}}{MP} \times 100$% where MP is marked Price |
|
To find Mark up Percentage |
Mark up % = $\frac {\text{Mark up value}}{CP} \times 100$% |
|
Selling Price with Profit% |
$S.P. = \frac{C.P. \times 100 + \text{Profit%} \times 100}{100}$ |
|
Selling Price with Loss% |
$S.P. = \frac{C.P. \times 100 - \text{Loss%} \times 100}{100}$ |
|
To calculate CP with Selling Price with Profit% |
$C.P. = \frac{S.P. \times 100}{100+ \text{Profit%}}$ |
|
To calculate CP with Selling Price with Loss% |
$C.P. = \frac{S.P. \times 100}{100-\text{Loss%}}$ |
Simple Interest (S.I.) & Compound Interest (C.I.):
Following are some basic and Important Formulas for CAT 2025 related to Simple Interest and Compound Interest:
|
Concept |
Formula |
|
Simple Interest |
For Principal ($P$), Rate of Interest ($R$), Time ($T$): $S.I. = P \times R \times T / 100$ |
|
Compound Interest (compounded annually) |
$A = P(1 + \dfrac{R}{100})^n$ where $n$ = time in years. |
|
Compound Interest (compounded half-yearly) |
$A = P \left(1 + \dfrac{R}{2 \times 100}\right)^{2T}$ |
|
Difference Between C.I. and S.I. (2 years) |
$C.I. - S.I. = P \left( \dfrac{R}{100} \right)^2$ |
|
Difference Between C.I. and S.I. (3 years) |
$C.I. - S.I. = P \left( \dfrac{R}{100} \right)^2 \left( 3 + \dfrac{R}{100} \right)$ |
Time, Speed & Distance:
Following are some basic and Important Formulas for CAT 2025 related to Time, Speed and Distance:
|
Concept |
Formula |
|
Relating speed, distance, and time |
Distance = Speed $\times$ Time |
|
Average Speed |
$\text{Average Speed} = \dfrac{\text{Total Distance}}{\text{Total Time}}$ |
|
Average speed when the distance covered in each stage of a journey is the same, but speeds are different |
$ \text{Average Speed} = \frac{2 s_1 s_2}{s_1 + s_2} $ |
|
Average speed when the time taken in each stage is the same but speeds differ |
$ \text{Average Speed} = \frac{s_1 + s_2}{2} $ |
|
Trains | |
|
Time for a train to cross a pole/person |
$T = \dfrac{l}{s}$; Where: $l =$ Length of the train, $s =$ Speed of the train |
|
Time for a train to cross a platform/tunnel |
$T = \dfrac{l + d}{s}$; Where: $l =$ Length of the train, $d =$ Length of platform/tunnel, $s =$ Speed of the train |
|
Time for trains to cross each other (same direction) |
$T = \dfrac{l_1 + l_2}{s_1 - s_2}$; Where: $l_1, l_2 =$ Lengths of Train 1 and Train 2; $s_1, s_2 =$ Speeds of Train 1 and Train 2 |
|
Time for trains to cross each other (opposite direction) |
$T = \dfrac{l_1 + l_2}{s_1 + s_2}$; Where: $l_1, l_2 =$ Lengths of Train 1 and Train 2; $s_1, s_2 =$ Speeds of Train 1 and Train 2 |
|
Boats and Stream | |
|
Distance (Downstream: same direction) |
$D = (x + y) \times t$ km where x is speed of boat in still water, y is the speed of stream and t is the time. |
|
Distance (Upstream: opposite direction) |
$D = (x - y) \times t$ km where x is speed of boat in still water, y is the speed of stream and t is the time. |
Circular Track:
If two people start from the same point on a circular track of length $D$ km with speeds $a$ & $b$ kmph.
|
|
Both are moving in same direction |
Both are moving in opposite direction |
|
Time of first meeting anywhere in the track |
$ t_{\text{first}} = \frac{D}{|a-b|} $ |
$ t_{\text{first}} = \frac{D}{a+b} $ |
|
Time to meet again at the starting point |
$ t_{\text{start}} = \text{LCM}\left(\frac{D}{a}, \frac{D}{b}\right) $ |
$ t_{\text{start}} = \text{LCM}\left(\frac{D}{a}, \frac{D}{b}\right) $ |
|
Number of distinct meeting points: |
$ \text{Meeting points} = |x - y| $ Where $x:y$ is the simplified ratio of speeds. |
$ \text{Meeting points} = |x + y| $ Where $x:y$ is the simplified ratio of speeds. |
Clocks
|
Concept |
Formula |
|
Speed of Hour Hand |
$0.5^\circ$ per minute |
|
Speed of Minute Hand |
$6^\circ$ per minute |
|
Angle between Hour and Minute Hands |
$\theta =|\frac{11}{2}M-30H$| |
Time and Work
Following are some basic and Important Formulas for CAT 2025 related to Time and Work:
|
Concept |
Formula |
|
Individual work |
If A can do work in x days: A’s rate = $\frac {1}{x}$ |
|
Combined Work |
If A and B work together: Combined rate = 1/x + 1/y; Time = 1 / (1/x + 1/y) = (x × y) / (x + y) |
|
Work rate |
Work = Rate × Time |
CAT Algebra Formulas
The Algebra section is a critical part of the Quantitative Aptitude section in the CAT exam. Below are over 50 important formulas for CAT preparation in this section, which are provided in this comprehensive CAT Formula Sheet:
Quadratic Equations
General form: $ ax^2 + bx + c = 0 $
Roots of the equation (Shreedhara Acharya's Formula): $ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $
Sum of roots: $ \text{Sum} = -\frac{b}{a} $
Product of roots: $ \text{Product} = \frac{c}{a} $
Discriminant: $ D = b^2 - 4ac $
-
If $D > 0$, roots are real and distinct
-
If $D = 0$, roots are real and equal
-
If $D < 0$, roots are imaginary and distinct
Progression & Series
|
Concept |
Formula |
|
nth term of an AP (First term = $a$, common difference = $d$) |
$T_n = a + (n-1)d$ |
|
Sum of the first $n$ terms of the A.P. |
Sum = Average of all the terms $\times$ number of terms $(n)$ $S_n = \dfrac{n}{2} \big[ 2a + (n-1)d \big]$ |
|
nth term of a GP ($a$ is the first term and $r$ is the common ratio) |
$T_n = a \cdot r^{n-1}$ |
|
Sum of the first $n$ terms of GP |
If $|r| < 1$: $S_n = a \cdot \dfrac{1-r^n}{1-r}$ If $r > 1$: $S_n = a \cdot \dfrac{r^n-1}{r-1}$ |
|
Sum of infinite terms of the G.P. |
(if $|r|<1$): $S_\infty = \dfrac{a}{1-r}$ Where: $a =$ first term, $r =$ common ratio, $n =$ number of terms |
|
Sum of first $n$ natural numbers |
$ 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} $ |
|
Sum of squares of first $n$ natural numbers |
$ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6} $ |
|
Sum of cubes of first $n$ natural numbers |
$ 1^3 + 2^3 + 3^3 + \cdots + n^3 = \left(\frac{n(n+1)}{2}\right)^2 $ |
|
Sum of first $n$ odd numbers |
$ 1 + 3 + 5 + \cdots + (2n-1) = n^2 $ |
|
Sum of squares of first $n$ even numbers |
$ 2^2 + 4^2 + 6^2 + \cdots + (2n)^2 = \frac{2n(n+1)(2n+1)}{3} $ |
|
Sum of squares of first $n$ odd numbers |
$ 1^2 + 3^2 + 5^2 + \cdots + (2n-1)^2 = \frac{n(2n+1)(2n-1)}{3} $ |
Indices & Surds
Product Rule: $ a^m \cdot a^n = a^{m+n} $
Quotient Rule: $ \frac{a^m}{a^n} = a^{m-n} $
Power of a Power: $ (a^m)^n = a^{mn} $
Power of a Product: $ (ab)^n = a^n \cdot b^n $
Power of a Quotient: $ \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} $
Negative Exponent: $ a^{-n} = \frac{1}{a^n} $
Logarithmic Rules and Properties
Definition of Logarithm:
$ \log_b a = x ;;\Longleftrightarrow;; b^x = a $
Log of 1: $ \log_b 1 = 0 \quad (b>0, ; b \neq 1) $
Log of the base itself: $ \log_b b = 1 $
Log of a product: $ \log_b (mn) = \log_b m + \log_b n $
Log of a quotient: $ \log_b \left(\frac{m}{n}\right) = \log_b m - \log_b n $
Log of a power: $ \log_b (m^n) = n \cdot \log_b m $
Change of base formula: $ \log_b a = \frac{\log_k a}{\log_k b} $
Base switch rule: $ \log_a b = \frac{1}{\log_b a} $
HCF and LCM
-
HCF of given fraction = $\frac{\text{HCF of numerators}}{\text{LCM of denominators}}$
-
LCM of given fraction = $\frac{\text{LCM of numerators}}{\text{HCF of denominators}}$
-
HCF x LCM= Product of the two numbers
-
If the H.C.F of the numbers a, b, c is K, then a, b, c can be written as multiples of K (Kx, Ky, Kz, where x, y, z are some numbers). K divides the numbers a, b, c, so the given numbers can be written as the multiples of K.
-
If the H.C.F of the numbers a, b is K, then the numbers (a + b), (a -b) is also divisible by K.
-
The numbers a and b can be written as the multiples of K, a = Kx, b = Ky.
(a + b) = (Kx + Ky) = K (x + y)
(a - b) = (Kx - Ky) = K(x – y)
Therefore, (a + b) and (a - b) is also divisible by the H.C.F of a, b.
CAT Geometry and Mensuration Formulas
Mastering important geometry formulas is crucial for cracking the CAT exam, as geometry and mensuration is a key topic in the Quantitative Aptitude section. The following section covers all essential CAT geometry and mensuration formulas:
Triangles:
Properties of Triangles:
-
The sum of any two sides is always greater than the third one and the difference of any two sides is less than the third one.
-
Let $a, b, c$ be the sides of a triangle, then $|b-c| < a < b+c$
-
In a scalene triangle the greatest side is always greater than one-third of the perimeter and less than half of the perimeter.
-
Let $a, b, c$ be the sides of the triangle and $a$ be the greatest side. Let the perimeter be $P$. Then
CAT 2025 College Predictor
Use CAT 2025 College Predictor to check your chances for IIM and top MBA calls based on CAT percentile, profile, work experience and cut-off trends.
Use Now$\dfrac{P}{3} < a < \dfrac{P}{2}$
-
For $a, b, c$ sides of a triangle and $a$ the greatest side:
If $a^2 < b^2 + c^2$, then the triangle is acute angled.
If $a^2 = b^2 + c^2$, then the triangle is right angled (Pythagoras theorem).
If $a^2 > b^2 + c^2$, then the triangle is obtuse angled.
Properties related to median
(Here $D$ is the midpoint of side $AC$, so $AD = DC$)
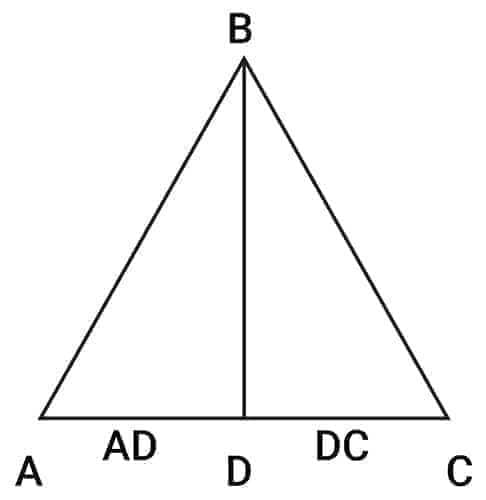
Midpoint of a triangle
-
Length of the Median –
BD = $\frac12 \sqrt{2(AB^2+BC^2)−AC^2}$ -
3× (Sum of squares of sides) =4× (Sum of squares of medians), that is,
$3(a^2+b^2+c^2)=4({M_a}^2+{M_b}^2+{M_c}^2)$
where a,b, and c are the sides of the triangle and Ma, Mb, and Mc are the medians. -
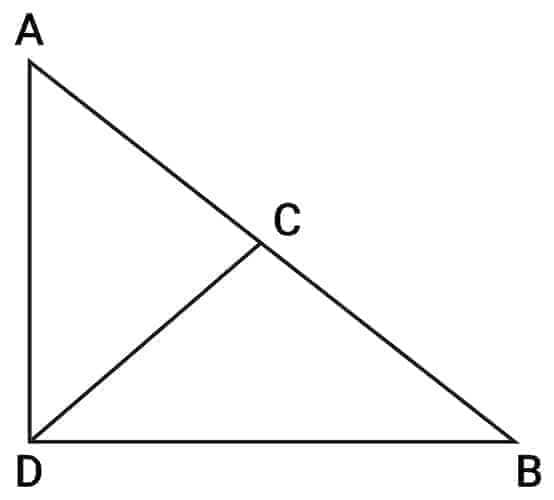
In a right-angled triangle, Median of Hypotenuse = Half of Hypotenuse
That is,
CD = AB/2
If all the medians are drawn in the triangle, then the 6 small triangles are generated in the triangle, which are equal in the Area.
Area of Triangle:
Heron’s Formula: Let $a, b, c$ be the sides of the triangle,
Area $= \sqrt{s(s-a)(s-b)(s-c)}$ where $s = \dfrac{a+b+c}{2}$ is the semiperimeter.
If two sides and the included angle are given:
Area $= \dfrac{1}{2} \times \text{(Product of given sides)} \times \sin(\text{included angle})$
Area $= \dfrac{1}{2} \times a \times b \times \sin C$
(Example: sides $a, b$ and included angle $C$ are given)
If a side and its respective altitude (perpendicular drawn from the opposite vertex) is given, then:
Area of the triangle $= \dfrac{1}{2} \times \text{Base} \times \text{Height (Altitude)}$
Area of an equilateral triangle = $ \frac{\sqrt{3}}{4} a^2 $
Height (Altitude) of an equilateral triangle = $ \frac{\sqrt{3}}{2} a $
Area of a triangle = $ r \times s $ (where $r$ is the inradius and $s$ is the semiperimeter)
Area of a triangle = $ \frac{abc}{4R} $ (where $a$, $b$, $c$ are sides and $R$ is the circumradius)
Quadrilaterals:
|
Trapezium
|
Area: $ \frac{1}{2} \times (\text{Sum of Parallel Sides}) \times \text{Height} $ |
|
Parallelogram
|
Opposite angles and sides are equal. |
|
Rhombus
|
All sides and opposite angles are equal. Diagonals bisect each other at 90∘. Sum of squares of diagonals: $ 4a^2 $ Where: |
|
Rectangle |
Perimeter: $ 2(l + b) $ (where $l =$ length, $b =$ breadth) |
|
Square |
Perimeter: $ 4a $ (where $a =$ side of square) |
|
Cyclic Quadrilateral
|
$\text{Sum of opposite angles} = 180^\circ$ $\text{Area} = \frac{1}{2} \times d_1 \times d_2 \times \sin \theta \quad \text{(where } \theta \text{ is the angle between the diagonals)}$ $\text{Area} = (s - a)(s - b)(s - c)(s - d), \quad \text{where } a,b,c,d \text{ are sides and } s = \frac{a + b + c + d}{2} \text{ is the semi-perimeter}.$ |
Circle:
Circumference of a circle $= 2\pi r$
Area of a circle $= \pi r^2$
For a semi-circle:
Circumference of a semi-circle $= \pi r$
Perimeter of a semi-circle $= \pi r + 2r$
Area of a semi-circle $= \dfrac{\pi r^2}{2}$
Sector & Segment of a circle
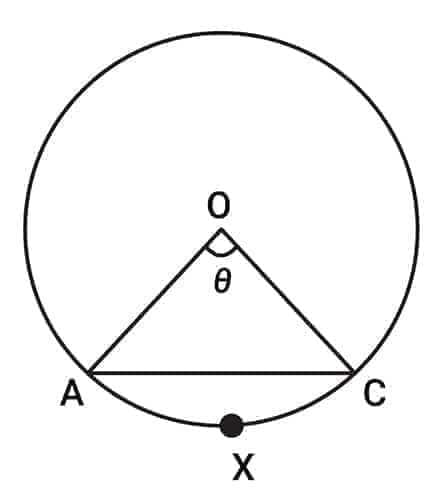
$OAXC$ is called the sector of the circle and $AXC$ is called the segment.
Length of arc $AXC = \dfrac{\theta}{360} \times 2\pi r$ (where $r$ is the radius)
Area of sector $OAXC = \dfrac{\theta}{360} \times \pi r^2$
$2 \times \text{Area of sector} = \text{Length of arc} \times \text{Radius}$
Area of segment $AXC = \text{Area of sector } OAXC - \text{Area of } \triangle OAC$
$A = \dfrac{\theta}{360} \pi r^2 - \dfrac{1}{2} r^2 \sin \theta$
Where:
$\theta$ = angle subtended at the center (in degrees)
$r$ = radius of the circle
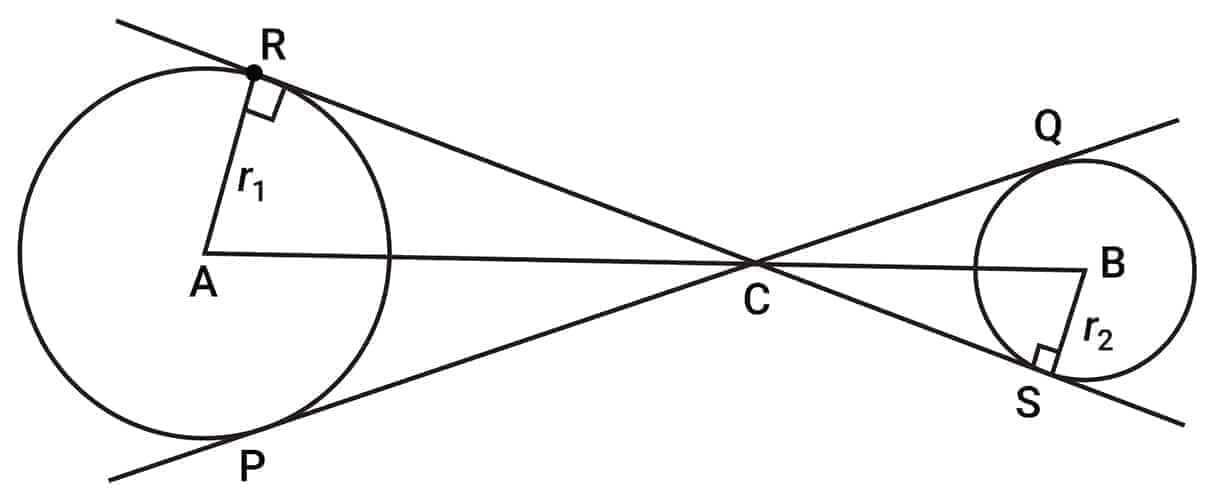
Common Tangent
$PQ$ and $RS$ are the direct common tangents of the circles, which are equal in length.
Length of direct common tangent $(L)$:
$L^2 = d^2 - (r_1 - r_2)^2$
Where:
$d =$ distance between centers of the circles
$r_1, r_2 =$ radii of the circles
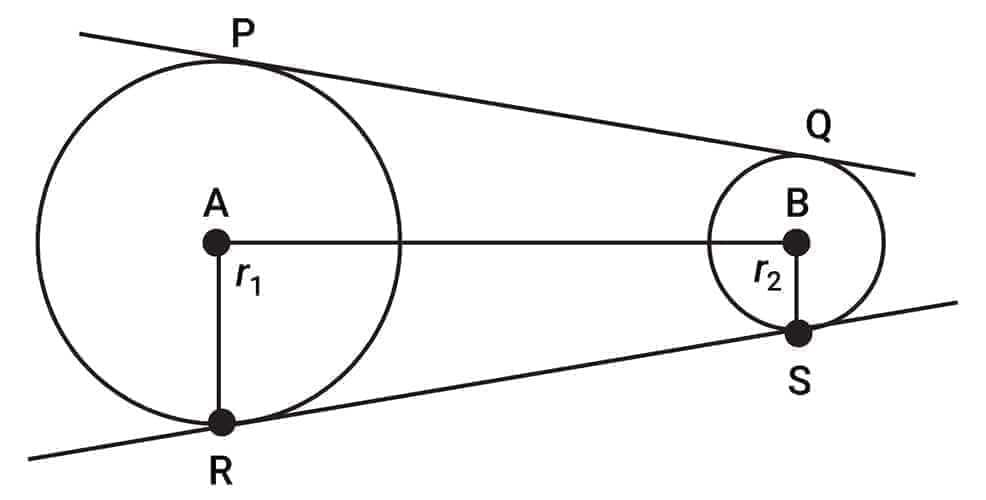
$PQ$ and $RS$ are the transverse common tangents of the circles, which are equal in length.
Length of transverse common tangent $(L)$:
$L^2 = d^2 - (r_1 + r_2)^2$
Where:
$L =$ length of the transverse common tangent
$d =$ distance between the centres of the two circles
$r_1, r_2 =$ radii of the two circles
Mensuration:
|
Cube {a- side of cube} |
|
|
Cuboid {l-length, b-breadth, h-height} |
|
|
Cylinder {r-radius of circular base, h-height} |
|
|
Cone {r-radius of circular base, h-height, l- slant height} |
Curved Surface Area (C.S.A.): $ \pi r l $ Total Surface Area (T.S.A.): $ \pi r (r + l) $ Volume: $ \frac{1}{3}\pi r^2 h $ |
|
Sphere {r-radius} |
Total Surface Area: $ 4\pi r^2 $ Volume: $ \frac{4}{3} \pi r^3 $ |
|
Hemi-sphere {r-radius} |
|
CAT Important Formulas of Trigonometry
Trigonometry plays a vital role in the CAT Quantitative Aptitude section, making it essential to learn and memorise key formulas. This comprehensive list of important CAT trigonometry formulas helps aspirants solve complex problems with speed, accuracy, and confidence during the exam.
1. Basic Trigonometric Ratios
These are defined in relation to a right-angled triangle:
$\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}$
$\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\csc \theta = \frac{\text{Hypotenuse}}{\text{Opposite side}}$
$\sec \theta = \frac{\text{Hypotenuse}}{\text{Adjacent side}}$
$\cot \theta = \frac{\text{Adjacent side}}{\text{Opposite side}}$
2. Pythagorean Identities
$\sin^2 \theta + \cos^2 \theta = 1$
$1 + \tan^2 \theta = \sec^2 \theta$
$1 + \cot^2 \theta = \csc^2 \theta$
3. Trigonometric Functions of Negative Angles
$\sin(-\theta) = -\sin \theta$
$\cos(-\theta) = \cos \theta$
$\tan(-\theta) = -\tan \theta$
$\csc(-\theta) = -\csc \theta$
$\sec(-\theta) = \sec \theta$
$\cot(-\theta) = -\cot \theta$
4. Angle Sum and Difference Formulas
$\sin(A + B) = \sin A \cos B + \cos A \sin B$
$\sin(A - B) = \sin A \cos B - \cos A \sin B$
$\cos(A + B) = \cos A \cos B - \sin A \sin B$
$\cos(A - B) = \cos A \cos B + \sin A \sin B$
$\tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}$
$\tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B}$
CAT Permutation& Combination and Probability Key Formulas
Permutation and Combination:
1. Number of permutations (or arrangements) of n different things taken all at a time = n!
2. Number of permutations of n things out of which $P_1$ are alike and are of one type, $P_2$ are alike and are of a second type and $P_3$ are alike and are of a third type and the rest are all different = $\frac{n!}{P_1!P_2!P_3!}$
3. Number of permutations of n different things taken r at a time when repetition is allowed = n × n × n ×… (r times) = n^r.
4. Total number of selections of zero or more things out of k identical things = k + 1.
5. Total number of selections of zero or more things out of n different things =
$n_(C_o ) + n_(C_1 ) + n_(C_2 ) + … + n_(C_n ) = 2^n$
6. The number of selections of 1 or more things out of n different things = $n_(C_1 ) + n_(C_2 ) + … + n_(C_n ) = 2^n-1$
7. Number of ways of arranging n people on a circular track (circular arrangement)
= (n – 1)!
8. Number of squares in a square of n × n side = $1^2 + 2^2 + 3^2 + 4^2 + … n^2$
9. Number of rectangles in a square of n × n side = $1^3 + 2^3 +3^3 + 4^3 + … n^3$
10. A rectangle having m rows and n columns:
The number of squares is given by:
m.n + (m – 1)(n – 1) + (m – 2)(n – 2) + ….. until any of (m –x) or (n – x) comes to 1.
The number of rectangles is given by: (1 + 2 + …… + m)(1 + 2 + …… + n)
Probability:
1. Probability of an Event
Let E be an event and S be the sample space. Then the probability of the event E can be defined as
P(E)=(n(E))/(n(S))
where P(E) = Probability of the event E, n(E) = number of ways in which the event can occur and n(S) = Total number of outcomes possible
2. 0 ≤ P (E) ≤ 1
P(ϕ) = 0 (∵ Probability of occurrence of an impossible event = 0)
3. Addition Theorem
Let A and B be two events associated with a random experiment. Then
P(A U B) = P(A) + P(B) – P(A ∩ B)
If A and B are mutually exclusive events, then P(A U B) = P(A) + P(B) because for mutually exclusive events, P(A ∩ B) = 0
4. If A and B are two independent events, then
P(A ∩ B) = P(A).P(B)
5. Odds on an event
Let E be an event associated with a random experiment. Let x outcomes are favourable to E and y outcomes are not favourable to E, then
Odds in favour of E are x:y,i.e.,x/y, and
Odds against E are y:x,i.e.y/x
P(E) = x/(x+y)
P(not E )=x/(x+y)
6. Conditional Probability
Let A and B be two events associated with a random experiment. Then, the probability of the occurrence of A given that B has already occurred is called conditional probability and denoted by P(A/B)
Example: A bag contains 5 black and 4 blue balls. Two balls are drawn from the bag one by one without replacement. What is the probability of drawing a blue ball in the second draw if a black ball is already drawn in the first draw?
Let A be the event of drawing a black ball in the first draw and B be the event of drawing a blue ball in the second draw. Then, P(B/A) = Probability of drawing a blue ball in the second draw given that a black ball is already drawn in the first draw.
Total Balls = 5 + 4 = 9
Since a black ball is drawn already,
Total number of balls left after the first draw = 8
Total number of blue balls after the first draw = 4
P(B/A) = 4/8=1/2
Download Now: CAT 2025 Quantitative Aptitude Cheat Sheet PDF
CAT 2025 Formula Sheet: Why You Need It?
In the last stage of preparation CAT 2025 formula sheet will help you to recall key concepts, save revision time, and improve accuracy in problem-solving. Having all important formulas from Arithmetic, Algebra, Geometry, and Modern Math in one place boosts your speed and confidence while attempting Quantitative Aptitude questions in the exam. It is helpful in the following ways:
-
Saves Time During CAT Revision
-
Strengthens Conceptual Clarity
-
Minimises Errors and Improves Accuracy
-
Enhances Mock Test Performance
-
Builds Confidence Before the Exam
CAT 2025 Recommended eBooks and Study Materials
Explore the best CAT 2025 eBooks and study materials recommended by experts for complete preparation. These resources will help aspirants revise efficiently and boost exam preparation.
|
Title |
Download Link |
|
CAT 2025 Quantitative Aptitude 20 Free Sectional Tests | |
|
CAT 2025 Arithmetic Important Concepts and Practice Questions | |
|
CAT 2025 Algebra Important Concepts and Practice Questions | |
|
CAT 2025 Quantitative Aptitude Study Material PDF - Geometry and Mensuration | |
|
CAT 2025 Number System Important Concepts and Practice Questions | |
|
CAT 2025 Quantitative Aptitude Questions with Answers PDF |
Articles
Related Stories
|
Upcoming Bschool Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Popular Courses and Specializations
List of colleges accepting CAT
Browse Bschool Colleges by State
Questions related to CAT
On Question asked by student community
Have a question related to CAT ?
FMS Udaipur admission for 2026 is not open. The MBA 2026 admission will likely commence in May 2026. You can keep checking the official website of FMS.
Hi admission to the courses offered at CUSAT is based on the CUSAT CAT results, relative performnace of the students and the number of applications for each course. Please check CUSAT CAT cutoff 2025 to know in detail about the cutoff score for Electrical and Electronic branch in previous years.
Yes, it is possible. If you have received a PI call from IIM Sambalpur with a 75 percentile in CAT, you have a chance to convert the call. However, the final selection will depend on multiple factors such as your personal interview performance, academic record, and overall profile.
All the
Hello
If you are looking to take admission in the MBA programme with a CAT score of 73, check out the list of MBA Colleges accepting 70-80 percentile .
All the best!
You can find all the information here:
CAT- https://bschool.careers360.com/articles/cat-exam-dates
SNAP- https://bschool.careers360.com/articles/snap-exam-dates
Popular CAT Questions
Directions for question :
M/s Deloitte Touche Tohmatsu Limited, one of the top four audit and accounting firms in the world with headquarters at London, UK, and with an operational presence in 153 countries, hires Management Trainees (MT) from all the premier management institutes of India thrice every year, in the months of January, May and September.
Each new group of Management Trainees (MT) have to go through a four month rigorous training schedule, after which they have to pass through a test consisting of a written assessment and a case-analysis. The top hundred ranked Management Trainees (MT) based on the performance in the test are confirmed as Management Executives (ME). The rest are given the opportunity of undergoing the training for four months one more time along with the next batch of Management Trainees (MT) and then passing through the subsequent test consisting of the written assessment and case-analysis. The Management Trainee (MT) who fails to get confirmed as a Management Executive (ME) the second time is fired.
The scatter-graph below depicts the number of Management Trainees (MT) at Deloitte taking the tests from January 2020 till May 2022, and the vis-à-vis hired Management Trainees (MT) at Deloitte who were fired :
It is also known that for the month of September 2019 at Deloitte, 96 hired Management Trainees (MT) failed to be confirmed as a Management Executive (ME) the first time, and that 36 hired Management Trainees (MT) were fired.
Question :
In which test did the minimum number of Management Trainees (MT) get confirmed as a Management Executive (ME) in the second attempt ?
Option: 1
September 2020
Option: 2
May 2021
Option: 3
January 2021
Option: 4
January 2022
Directions for question:
The bar-graph given below shows the foreign exchange reserves of Nepal (in million Rupees) from 2014 to 2021. Answer the following questions based on the graph :
Question:
What was the percentage increase (rounded to the nearest integer, if deemed necessary) in the foreign exchange reserves in 2020 over 2016 ?
Option: 1 None
Option: 2 None
Option: 3 None
Option: 4 None
MBA/PGDM Admissions OPEN
Amity University-Noida MBA Admissions 2026
ApplyRanked among top 10 B-Schools in India by multiple publications | Top Recruiters-Google, MicKinsey, Amazon, BCG & many more.
Karnavati University MBA Admissions 2026
ApplyIndustry Internship Training
ITM Business School MBA Admissions 2026
Apply400+ Company Visits | Highest CTC Offered: 21 LPA | Average CTC Offered: 8.65 LPA | 100% Placement Assurance
Manav Rachna-MBA Admissions 2026
ApplyRecognized as Category-1 Deemed to be University by UGC | 41,000 + Alumni Imprints Globally | Students from over 20+ countries
SRM University Chennai BBA/MBA
ApplyNAAC A++ Accredited | Ranked #12 by NIRF
UPES MBA Admissions 2026
ApplyLast Date to Apply: 26th March | Ranked #36 amongst institutions in Management by NIRF | 100% Placement
CAT Notifications
Never miss CAT update
Get timely CAT updates directly to your inbox. Stay informed!