CAT Admit Card Date:05 Nov' 25 - 30 Nov' 25
Master DILR for CAT 2025 begins with understanding how this section blends data analysis and logical reasoning to test real analytical intelligence. The CAT DILR 2025 practice questions challenge you to interpret complex charts, puzzles, and caselets where no single formula works. Every set demands clarity of thought, quick comprehension, and structured problem-solving. Candidates must practice at least one set of DILR every day to boost their scores in CAT 2025.
This Story also Contains
In this article, we have discussed:
CAT 2025 DILR exam strategy
Questions One Can Expect in CAT DILR 2025
Logical Reasoning and Data Interpretation shortcut tricks
The CAT 2025 DILR section is known for its challenging puzzles and data sets that test logical thinking, interpretation skills, and time management. Below are the key highlights you must know.
Section | Detail |
Total Questions in DILR | 22 |
Total Time for Section | 40 minutes |
Division of Questions | 5 sets (3 sets of 4 questions and 2 sets of 5 questions) |
Marking Scheme | +3 for a right answer -1 for a wrong answer No negative marking for TITA |
The CAT 2025 DILR section tests problem-solving, logical thinking, and data interpretation skills, making it one of the toughest parts of the exam. A smart strategy, consistent practice, and clarity in approach are key to mastering it. Here’s a focused plan to crack DILR with confidence.
In the Data Interpretation and Logical Reasoning section, time management starts with smart selection. The first two to three minutes should be spent scanning all the sets and marking the ones that look both familiar and logically approachable. This is where the Familiarity–Complexity Index helps—choose sets that you have practised before or ones that look simple. For example, a simple arrangement puzzle or a bar graph-based DI set may be quicker to solve than a game theory or complex Venn diagram set. By identifying the right sets early, you build confidence and save precious time for higher accuracy.
Many aspirants make the mistake of deciding beforehand that they will attempt certain types of sets, like arrangements or Venn diagrams. However, the CAT 2025 exam is unpredictable, and a familiar-looking set may turn out to be lengthy or tricky. The key is adaptability. Enter the section with an open mind and let the paper decide your moves. If a set appears too dense or calculation-heavy during the exam, skip it immediately instead of sticking to your preconceived plan.
Each DILR set generally contains 4 or 5 questions. Instead of approaching them as a block, treat them as individual opportunities. Sometimes, the first two questions of a set can be solved with partial information without needing the entire puzzle solved. For instance, in a table-based DI set, one question might only require a ratio or a percentage comparison, which can be solved independently. Adopting this question-wise lens ensures that you extract maximum marks from each set, even if you cannot complete it fully.
Attempting all questions in a CAT 2025 DILR set may look efficient, but in practice, it often consumes extra time and leads to errors. A smarter approach is to solve the ones you can crack confidently. For example, if a set has five questions, two may be solvable within minutes while the remaining three require complex calculations. Rather than pushing through the entire set, answer what you can and move on. This approach keeps your attempt count high, improves accuracy, and reduces mental fatigue.
One of the most overlooked strategies is having a stop-loss rule, which means knowing when to quit a set. If you find yourself spending more than 8–10 minutes on a single set without clear progress, it is time to leave it. Holding on to a difficult set often leads to time drain and missed opportunities elsewhere. By applying stop-loss, you stay in control of your timing, ensure wider coverage of sets, and keep your confidence intact throughout the section.
The CAT 2025 DILR (Data Interpretation and Logical Reasoning) section is one of the most dynamic and unpredictable parts of the exam. It tests how well you can understand complex data, connect clues, and reach conclusions quickly. Each set contains 4–6 questions based on logical puzzles, numerical data, or reasoning scenarios. The difficulty lies not in formulas but in interpreting the problem smartly and thinking critically.
Data Interpretation questions are based on numerical data shown through tables, bar graphs, line charts, or pie charts. The task is to analyse the data and perform quick calculations like percentage change, ratios, and comparisons.
These questions test your ability to process information visually and numerically. Usually, each DI set presents large data with multiple layers, making approximation and elimination key tools for accuracy.
Example:
A chart shows quarterly profits (in ₹ lakh) of four companies—A, B, C, and D—from 2019 to 2022.
Identify which company had the most consistent growth.
Find the average annual profit of company C.
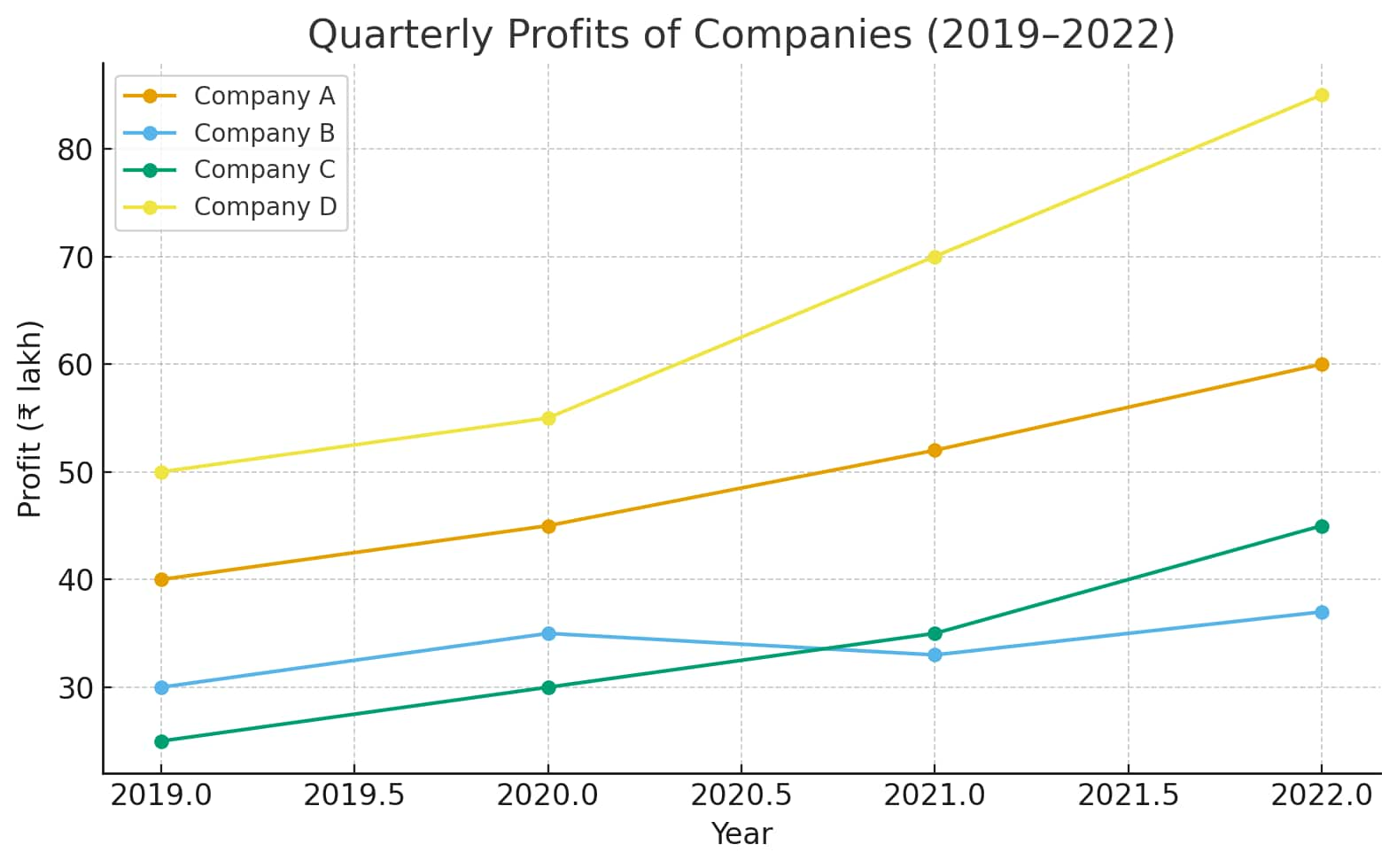
Here’s the illustrative graph showing the quarterly profits of Companies A, B, C, and D from 2019 to 2022.
From the trend lines:
Company A shows the most consistent growth over the years.
Average annual profit of Company C = (25 + 30 + 35 + 45) / 4 = ₹33.75 lakh.
Admissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
Ranked No. 3 Business School in India and no.35 in world by Financial Times MiM 2025 Ranking | Highest CTC: INR 89 LPA
Caselet questions replace graphs with paragraph-style information, often mixing data points and conditions. You must extract, arrange, and sometimes infer missing values before solving.
These are popular in CAT because they test comprehension and logical data structuring, not just calculation.
Example:
A company has three sales regions—North, South, and West.
The total sales are ₹12 crore.
South’s sales are twice that of West.
North’s sales are ₹2 crore less than South.
Find the sales figures for each region.
Arrangement-based reasoning sets are classic CAT favourites. You’ll get clues about people, seats, objects, or days, and must use logic to form a correct sequence.
These sets test your ability to combine multiple conditions without contradiction.
Example:
Seven friends—A, B, C, D, E, F, and G—are sitting around a circular table.
C sits to the right of D.
F is not next to G.
A is opposite E.
Find who sits between B and D.
Puzzle sets appear as short story problems with multiple variables like people, days, subjects, or items. These questions combine logic, sequencing, and sometimes numerical reasoning.
They can be time-consuming, but once the logic clicks, the entire set becomes easy to solve.
Example:
Five employees—Riya, Aman, Neel, Priya, and Karan—work in five departments: HR, Finance, IT, Sales, and Legal.
Riya is not in IT or Legal.
Aman works in a department next to Neel’s.
Priya’s department is before Karan’s alphabetically.
Determine each person’s department.
These involve overlapping groups or categories, testing your ability to calculate intersections, unions, and exclusive areas. They combine logic and quick arithmetic.
Example:
In a survey of 300 students:
180 like Tea,
120 like Coffee,
80 like both Tea and Coffee.
How many like only Tea?
Solution Idea:
Only Tea = 180 – 80 = 100.
This type of question checks your understanding of logical overlap and total count.
Game and tournament sets are logical reasoning problems framed around matches, points, and rankings. You may get round-robin (everyone plays everyone) or knockout (winner advances) scenarios.
Example:
In a football tournament, each team plays every other team once.
A win gives 3 points, a draw 1 point.
Team X ends with 10 points, and Team Y with 8 points.
How many matches could have been drawn?
These sets involve if–then statements, conditions, and inferences. They check how precisely you can apply logic without assumptions.
Example:
Statements:
All engineers are graduates.
Some graduates are artists.
Conclusions:
A. Some engineers are artists.
B. Some artists are graduates.
Which conclusion logically follows?
Solution Idea:
Only conclusion B is correct. These problems test conceptual clarity in deductive reasoning.
Recent CAT papers include hybrid sets that blend data interpretation and reasoning. You may need to decode conditions and calculate numbers simultaneously.
Example:
A company organises 4 workshops—A, B, C, and D—attended by managers from three cities. The total revenue and participation vary across workshops, and attendance depends on day-wise schedules.
You may be asked to:
Find the city contributing maximum revenue,
Identify the day with minimum total participation.
Some CAT 2025 questions include advanced versions of arrangements with additional constraints such as colour, timing, or location. These require multi-layered reasoning.
Example:
Four friends—A, B, C, and D—live in different cities (Delhi, Pune, Mumbai, Chennai) and own cars of different colours.
A doesn’t live in Delhi or own a red car.
The one in Pune owns a blue car.
D owns a green car and doesn’t live in Chennai.
Determine the city and car colour of each person.
Sometimes, CAT introduces data sufficiency problems, where you decide whether the given data is adequate to answer a question—not necessarily find the answer itself.
Example:
Question: What is the ratio of A’s salary to B’s salary?
Statement 1: A earns ₹10,000 more than B.
Statement 2: A’s salary is ₹50,000.
You must check if one, both, or neither statement provides enough data.
The Data Interpretation and Logical Reasoning (DILR) section in CAT 2025 is designed to test analytical ability, logical thinking, and decision-making skills. Many students find this section challenging, but with the right preparation strategy, it can be mastered.
One of the most effective ways to prepare for the DILR section is to solve original CAT papers. Working through at least 15 CAT previous year question papers gives you exposure to more than 60 sets, each designed in the actual exam pattern. Solving them as sets rather than isolated questions helps you understand the exam’s flow, time pressure, and the mix of difficulty levels. It also familiarises you with recurring concepts, so you know what types of problems CAT prioritises year after year.
In addition to past papers, taking CAT 2025 Mock Tests is essential for building speed, accuracy, and endurance. Each mock simulates the actual exam environment, which helps reduce exam-day anxiety. The key here is not just solving every set but also analysing and revising them. Reviewing mistakes, understanding shortcuts, and identifying alternative solving methods is what makes mocks valuable. This process ensures steady improvement and teaches you how to adapt to unexpected question types.
Consistency is critical for mastering DILR. A simple yet powerful habit is to solve at least 2 sets a day. This daily practice keeps your logical reasoning and calculation skills sharp, while also building stamina for exam day. By gradually increasing the complexity of the sets you attempt, you strengthen both accuracy and speed. Over time, this routine ensures that solving sets becomes second nature.
The latest types of sets in CAT Data Interpretation (DI) have evolved to test not only mathematical ability but also logical reasoning and data comprehension. Unlike traditional simple calculations, these sets now combine tables, graphs, and caselets with logical twists. Know the details of the latest kinds of questions asked in CAT 2025.
These sets present a small story or situation in words, supported by a table containing numerical data. Candidates are usually asked to work with ratios, numbers, and percentages. The challenge here is linking the narrative with the table correctly. For example, a caselet may describe sales of products across regions while the table lists quantities, and you may need to calculate percentage growth or comparisons.
In this type, tables are given with some data deliberately left blank. The candidate must identify the relationship between existing values and then fill in the missing numbers. Solving these requires quick pattern recognition, basic arithmetic, and logical deductions. Often, one missing value is the key to solving the rest of the table.
This is a hybrid question type where a simple calculation alone will not work. The data is structured in a way that requires logical deductions along with numerical processing. For example, you may have data about teams playing matches, and alongside interpreting the scores, you must also apply reasoning to figure out rankings or results. These sets demand both sharp reasoning and numerical skills, making them relatively tougher.
Bar charts in CAT are rarely simple and direct. Instead of direct comparisons, they usually come with logical conditions or require multi-step reasoning. For example, you might be asked to calculate which product had the highest growth percentage, or to compare profits across years where values are interlinked. They test your ability to combine visual understanding with numerical accuracy.
Scatter plots display data as points across two axes. Questions usually involve finding trends, identifying correlations, or comparing distributions. Candidates must be quick at reading the graph, spotting outliers, and interpreting relationships such as whether an increase in one variable leads to an increase or decrease in another.
Also known as radar charts, spider graphs spread data across multiple categories radiating from a centre point. Candidates must compare values along different axes and interpret the overall shape of the graph. These are tricky because they involve multiple variables at once, demanding careful observation and comparative analysis.
In matrix-based sets, data is arranged in rows and columns, similar to a table but more complex. Each cell may represent a relationship between two variables. The challenge lies in cross-referencing data, applying arithmetic, and sometimes filling missing values. These sets test structured thinking and require patience as well as precision.
Pure caselets provide no tables, graphs, or charts. Instead, all information is written in paragraphs. Candidates need strong comprehension skills to extract key details and organise them logically before solving. These sets are time-consuming if you are not comfortable with reading dense text, but with practice, they can be scored since the logic is often simple once structured properly.
The traditional types of DI sets continue to appear in CAT exam, even though the exam has increasingly shifted towards logical and mixed-format questions. These sets are mostly chart or table-based and focus on numerical interpretation, percentages, and comparisons. For aspirants, they remain crucial because they are relatively direct and can be solved faster with practice, making them a reliable scoring area.
These sets display data using bar charts where values are expressed in percentages. Candidates need to quickly calculate proportions, compare categories, and interpret percentage changes. For example, sales distribution across regions may be shown in percentages, requiring you to compute actual values or growth.
Unlike percentage-based bar charts, these use actual numerical values. Questions often ask for differences, averages, or growth rates between categories. They are generally simple, provided candidates are comfortable with basic arithmetic and ratio analysis.
Line graphs represent data trends over time, often involving multiple lines for comparison. Questions usually revolve around growth rates, maximum or minimum values, and crossovers between two or more variables. They test the ability to interpret trends quickly and draw comparisons across time periods.
Pie charts represent data as circular sectors, usually in percentages. Candidates may need to calculate actual values from percentages, compare sectors, or combine data across multiple pies. These sets test accuracy in percentage-to-value conversions and proportional reasoning.
In stacked bar charts, each bar is divided into multiple sections, representing sub-categories. Candidates must interpret both the whole and its parts. For example, a company’s revenue bar may be stacked with contributions from different product categories, and questions could involve total revenue or percentage contribution from each segment.
These are less common but require interpreting data distributed across a triangular diagram, often involving three interdependent variables. The challenge lies in understanding the geometric structure and applying logical reasoning to extract information.
These tables present cumulative data, such as population or scores in ranges. To answer questions, candidates need to work backwards from cumulative values to find individual frequencies. They test precision, as even small mistakes in deduction can mislead the entire solution.
These sets feature multiple pie charts, often embedded within a larger chart or dataset. They require cross-referencing between different pies and calculating combined values or proportions. Such sets test both comprehension and the ability to connect multiple sources of information.
Multi-chart sets combine two or more chart types, such as bar graphs, line graphs, and pie charts, in a single set. Candidates must switch between formats and synthesise data to solve. These sets are highly representative of real-world data presentation and test adaptability as well as numerical skills.
The CAT 2025 DILR section carries significant weight in overall scoring, making it essential to focus on high-yield topics. Understanding which areas frequently appear in exams and practising them rigorously can boost your CAT 2025 DILR percentile. Here is a look at the top scoring topics in CAT 2025 DILR section.
Bar and line graphs frequently appear in 6–8 DILR questions per CAT exam, forming a significant part of Data Interpretation. Candidates often face questions involving trend analysis, percentage change, and comparative reasoning. Accurate interpretation of axes, scales, and data points allows for faster calculation and higher scoring opportunities in CAT DI questions.
Seating and arrangement problems account for 5–6 Logical Reasoning questions in CAT 2025, often testing logical deduction and constraint application. Linear and circular arrangements, multiple rows, and layered setups require careful visualisation. These high-scoring CAT LR questions reward aspirants who apply a structured approach.
Data sufficiency questions appear in 3–5 questions per CAT 2025 DILR section. They test whether the information provided is adequate to answer a query, requiring strong analytical skills rather than heavy computation. Accuracy in these CAT 2025 DILR questions can directly impact the overall CAT percentile score, as they are generally easier for aspirants.
Tables and caselets usually contribute 2–5 high-scoring questions in the Data Interpretation section. These involve interpreting complex tabular data or multi-step case-based scenarios. High scorers focus on extracting only the necessary information and identifying patterns, which allows them to solve CAT DI caselet questions efficiently.
Blood relation puzzles generally appear in 1–3 Logical Reasoning questions per CAT exam, testing logical deduction. Converting verbal descriptions into family trees or diagrams helps aspirants visualise relationships quickly. These high-yield CAT LR questions are scoring because precise analysis often solves the entire set correctly.
Puzzles, including grouping and distribution problems, appear in 1–2 questions per CAT 2025 DILR section. They require logical deduction and pattern recognition. Despite their smaller number, these high-scoring CAT LR puzzles are valuable as they often have fewer traps compared to other LR topics.
Clock and calendar questions typically make up 1–2 questions in CAT Logical Reasoning. They test time calculation, day-date identification, and angles of clock hands. Candidates who can quickly apply formulas and identify patterns gain an edge in scoring high in CAT 2025 DILR.
Assumptions or binary logic questions are less frequent, appearing in 1–2 questions per CAT exam. They test critical reasoning, decision-making, and conditional logic. Understanding the underlying rules allows aspirants to answer confidently, making them reliable high-scoring CAT 2025 DILR questions.
Syllogisms and Venn diagram-based questions usually appear in 1–2 questions per CAT 2025 DILR. These require careful analysis of logical statements and set relations. Accurately translating statements into diagrams allows aspirants to identify intersections and exclusions quickly, contributing to a higher CAT 2025 DILR percentile score.
Game theory or tournament scheduling questions are rare, around 1–2 questions per CAT LR section, but are often high scoring. They involve understanding sequences, match outcomes, or round-robin formats. Clear pattern recognition and logical analysis help aspirants solve these high-scoring CAT 2025 DILR questions correctly in minimal time.
Cracking the CAT 2025 DILR section requires consistent practice, a clear strategy, and targeted focus on Data Interpretation (DI) and Logical Reasoning (LR) questions. Aspirants must balance speed, accuracy, and problem-solving skills while tracking performance daily. A structured approach ensures better preparation and improves the overall CAT percentile. Get the detailed daily plan for the exam below.
Start with 2–3 DI sets covering graphs, tables, and charts. Focus on recognising question patterns, applying calculation shortcuts, and solving within strict time limits. Track which types take longer and note methods to solve them faster.
Attempt 1–2 LR puzzles such as seating arrangements, blood relations, or series problems. Analyse reasoning steps, identify shortcuts, and note common traps to avoid repeated mistakes.
Solve a complete DILR set from previous CAT exams or quality mock tests. Time each question, mark mistakes, and immediately review solutions to understand gaps in approach.
Solve smaller sets of 10–15 mixed DI/LR questions. Focus on maintaining high accuracy while reducing the time per question. Reinforce techniques for quick elimination and mental calculations.
Maintain an error log for all DI and LR questions. Record which shortcuts, patterns, or strategies worked, and revise them to ensure they are retained for the actual CAT exam.
Data Interpretation (DI) is one of the most crucial parts of competitive exams because it tests a candidate’s ability to analyse numbers, graphs, and patterns logically. Instead of memorisation, DI requires speed, accuracy, and the ability to apply concepts quickly. To master DI, one must focus on key concepts like gathering information, interpreting graphs, performing quick calculations, and drawing correct inferences.
The first step in DI is to observe the given data. This may be in the form of tables, charts, or graphs. A good student does not jump straight to solving but spends time identifying key figures, units, and patterns. This ensures that no information is overlooked and helps in avoiding silly mistakes later.
After gathering information, the next step is to interpret the chart correctly. This means understanding what the graph represents, whether it shows growth, comparison, percentage distribution, or trends over time. Misreading the graph can lead to wrong answers, so accuracy here is essential. For example, one should check whether the values are in percentages or absolute numbers before starting calculations.
DI questions are not just about reading numbers; they are about finding meaning. Students must analyse the given data to extract useful inferences. This involves identifying relationships, trends, and conclusions that can be drawn from the numbers. For example, if sales figures are given for five years, one should be able to infer the year with maximum growth or decline.
Once the inference is clear, solving the questions requires accurate and quick calculations. These may include operations such as addition, subtraction, multiplication, division, or percentage changes. Efficiency here depends on a strong command of basic mathematics. Quick mental math helps save precious time during exams where every second counts.
Many DI questions require cumulative or comparative results, which heavily rely on addition and subtraction. For example, summing values across categories or finding differences between two years’ figures. Accuracy in these basic operations is the backbone of solving DI correctly, as even a small mistake can change the entire answer.
Speedy multiplication is crucial in DI, especially when working with large numbers. Often, approximations can be used to save time, provided the answer options allow it. Developing mental multiplication tricks and practising Vedic maths techniques can significantly improve performance in this area.
Most DI problems involve percentages—whether it’s calculating growth, profit, loss, or proportion. A clear understanding of percentage increase and decrease helps in analysing changes over time. For example, knowing whether a 25% increase on 80 gives the same result as a 20% increase on 100 is vital to avoid errors.
A strong foundation in number properties makes DI calculations faster. Knowing prime numbers under 100, squares up to 20, and basic divisibility rules reduces the time taken for mental math. For instance, identifying whether a number is divisible by 3 or 11 instantly can save valuable seconds in exams.
The latest types of Logical Reasoning sets in CAT reflect evolving exam trends and test a candidate’s ability to handle complex, time-bound puzzles. Below are the important set types you should practice.
This type involves placing people or objects in a specific order, either in a straight line or in a circle, based on given clues. These clues might specify positions relative to each other (like who is to the left or right of whom), fixed placements, or proximity between entities. The primary focus is on determining the exact sequence or positioning while satisfying all constraints.
This is a hybrid category where individuals or items are both arranged and grouped simultaneously. In addition to deciding the order, you also need to categorise the elements into different sets, teams, or rows. Questions often involve multiple layers of logic—such as who sits where and belongs to which group—making them more complex than basic arrangements.
Here, the objective is to divide a given set of elements into different groups or distribute them across categories, often under certain rules. Unlike arrangements, there’s no inherent order, but the grouping itself must follow logical conditions. These puzzles test your ability to manage combinations and exclusions efficiently across different partitions.
These puzzles involve matching multiple attributes (like name, city, color, profession, etc.) across a table or grid using a series of interrelated clues. Solving them typically requires cross-referencing information and making eliminations until a complete set of correct pairings is achieved. They demand attention to detail and systematic deduction.
This set type deals with scheduling tasks or events based on dependencies and time constraints. You’ll often be given a series of activities with specific rules on what must come before or after others. The goal is to create a valid sequence or timeline that satisfies all conditions. These are similar to project management scenarios, testing your planning and sequencing skills.
Based on Venn diagrams, these problems involve categorising data into four overlapping sets. You must use logical reasoning and data interpretation to determine intersections, unions, and exclusions among the sets. Questions typically ask for the count of elements that belong to specific combinations of sets or none at all, requiring careful visual and logical analysis.
These puzzles are centred around competitions, where teams or individuals play against each other under certain formats like round-robin or knockout. You're given results, scores, or rankings, and must deduce outcomes such as who qualifies, who is eliminated, or the final standings. These CAT Games and Tournaments questions test analytical thinking and often involve arithmetic calculations.
This is a catch-all category for unique or non-standard puzzles that don’t fit into the conventional types. They may involve custom rules, logical sequences, or creative constraints. These games challenge your adaptability and reasoning skills by presenting unfamiliar formats where the usual templates may not apply.
These involve placing people or objects in a specific linear sequence based on given constraints. The goal is to determine the exact position of each element while following conditions like who is to the left/right of whom, fixed spots, or proximity rules. This is a foundational seating arrangement set type and often forms the basis for more complex puzzles.
A variation of linear arrangements, this set type involves placing elements around a circle. The circular nature introduces challenges like relative positioning (clockwise/anticlockwise) and no fixed starting point unless stated. These puzzles test your spatial reasoning and ability to handle symmetrical logic structures.
This Ranking and Ordering type focuses on determining the relative or absolute ranks, heights, weights, or scores of individuals based on comparison-based clues. You may need to arrange them in ascending/descending order, find ranks from either end, or determine positions using partial information. These puzzles test analytical and comparative reasoning.
These problems involve paths, routes, or connections between locations. You're often given a network of nodes (cities, intersections, points) with paths and must determine the shortest route, the number of possible paths, or whether a journey is possible under certain conditions. It tests spatial awareness and path optimisation logic.
These are classic Venn diagram-based puzzles involving 2 or 3 overlapping sets. You’re given numerical data and must determine how many elements lie in which section (e.g., only A, both A and B, all three sets, none). These questions test your ability to work with intersections, unions, and logical deduction from partial data.
Binary logic puzzles involve statements made by people that can be either true or false, and you must determine who is lying and who is telling the truth. Often based on specific character traits (e.g., truth-teller always tells the truth, liar always lies), these puzzles require deep logical deduction and scenario testing.
These cube puzzles involve visualisation of cubes—painted, cut, folded, or rotated. You may be asked to identify patterns on faces, the number of smaller cubes with certain properties, or determine views after certain movements. This set tests 3D spatial reasoning and the ability to manipulate objects mentally.
Logical Reasoning (LR) is an essential part of aptitude and competitive exams, as it evaluates a candidate’s ability to think logically, analyse patterns, and solve problems systematically. Unlike pure mathematics, LR is more about reasoning skills and structured thinking. Know more about the important concept of CAT Logical Reasoning below.
Connectives involve logical statements linked by words like and, or, if–then, either–or, neither–nor. These help form compound statements and test your ability to derive valid conclusions. Mastering connectives is crucial for solving reasoning puzzles, truth-based statements, and critical reasoning questions.
Syllogisms are problems where you conclude given statements, often involving categories like “All, Some, None.” Deduction involves applying rules of logic to arrive at definite or possible conclusions. These are common in exams to test both accuracy and speed in reasoning.
This concept deals with arranging or distributing people, objects, or tasks according to given conditions. For example, seating arrangements (linear or circular), assigning tasks, or distributing items. Such problems test your ability to organise information systematically while following constraints.
These problems involve finding the highest or lowest possible value under certain conditions. For instance, identifying the maximum marks a student can score or the minimum number of attempts needed. This Maxima and Minima concept helps sharpen optimisation skills in reasoning.
Permutation refers to arranging objects in order, while combination refers to selecting objects without order. LR uses these concepts in puzzles, seating arrangements, and probability-based reasoning. Understanding this helps in handling complex distribution and arrangement questions effectively.
Set theory problems involve groups, overlaps, and relationships, often represented using Venn diagrams. They test your ability to handle union, intersection, and complement of sets. These are especially useful in solving data grouping and classification problems.
Tournament-based problems test logical and mathematical reasoning by analysing match structures.
Round Robin: Every participant plays with every other participant once.
Knock Out: Players get eliminated after losing a match, and the last remaining player is the winner.
These require careful counting of matches, winners, and eliminations.
Binary logic deals with truth-tellers (always speak the truth) and liars (always lie). Problems involve identifying who is lying and who is truthful based on given statements. It sharpens reasoning ability and logical deduction skills.
Cubes involve 3D visualisation, painting, cutting, or unfolding cubes into nets. Such problems test spatial ability, visualisation, and logical deduction. These are very common in LR sections to evaluate mental rotation and 3D reasoning.
In CAT 2025 Data Interpretation (DI) sets, aspirants often lose marks not because of difficulty but because of inefficient calculation strategies. Most DI sets involve tables, bar/line graphs, pie charts, and caselets that require multiple interrelated calculations.
The key is prioritising question sequences and recognising computation shortcuts unique to CAT DI. Here are some go-to time-saving techniques to master CAT 2025 DILR:
In tables and caselets, check which questions use the same rows or columns. Solve shared calculations once to answer multiple questions.
For bar or line graphs, extract only the key points needed for comparison instead of plotting every value.
In trend-based graphs, calculate relative differences between adjacent bars or points rather than absolute values for faster results.
Solve the simpler questions that rely on direct data reading first to secure marks quickly.
Convert percentages into easy fractions like 1/4, 1/2, or 3/4 to eliminate complex multiplications.
When totals are required across rows or columns, sum once and reuse for all dependent questions instead of recalculating.
Multi-part caselets often follow patterns like max/min, difference, or ratio-based relationships; spotting these reduces redundant calculations.
In CAT 2025 Logical Reasoning (LR) sets, aspirants often face seating arrangements, blood relations, scheduling, and grouping puzzles that are multi-layered. High accuracy comes not from rote practice but from recognising set structures, dependency chains, and recurring patterns in CAT LR questions.
Knowing how to approach each type systematically can significantly increase the number of attempted questions and overall CAT 2025 DILR percentile.
For linear or circular arrangements, immediately draw a rough diagram marking fixed positions and relative constraints. This allows all subsequent sub-questions to be answered faster.
In multi-part puzzles, recognise which sub-questions can be solved independently and which rely on a common solution. Solve independent questions first to secure marks.
Convert verbal descriptions into a family tree, and eliminate impossible relationships systematically rather than testing all possibilities.
In problems like task or tournament scheduling, create a table with time/order constraints; this reduces repeated calculations for each question.
Many grouping or allocation puzzles hinge on identifying maximum or minimum constraints first; marking these speeds up the rest of the solution.
In conditional puzzles, convert statements into yes/no or true/false variables to quickly test combinations without recalculating.
Many CAT LR sets are multi-part; once the main configuration is finalised, all dependent questions can be solved with minimal extra effort.
The Data Interpretation and Logical Reasoning (DILR) section in CAT 2025 comprises 22 questions, accounting for 66 marks. This section is divided into two main areas: Data Interpretation (DI) and Logical Reasoning (LR), each contributing approximately 50% to the total weightage.
Section | Topic | Number of Questions | Approx. Weightage |
Data Interpretation (DI) | Bar Graphs & Column Charts | 6 | 30% |
Pie Charts & Percentage Distributions | 3 | 15% | |
Tables & Caselets | 2 | 10% | |
Line Graphs & Trend Analysis | 2 | 10% | |
Radar Charts & Bubble Charts | 2 | 10% | |
Data Sufficiency | 3 | 15% | |
Logical Reasoning (LR) | Seating Arrangements (Linear & Circular) | 4 | 20% |
Blood Relations & Direction Sense | 2 | 10% | |
Puzzles (Floor, Scheduling, etc.) | 3 | 15% | |
Syllogisms & Venn Diagrams | 2 | 10% | |
Binary Logic & Assumptions | 2 | 10% | |
Games & Tournaments | 2 | 10% | |
Clocks & Calendars | 2 | 10% |
Cracking the CAT 2025 DILR section is less about brute force and more about strategy, pattern recognition, and mental agility. Success comes from understanding which sets to attempt, how to organise complex data quickly, and how to maintain accuracy under time pressure. With 22 questions in 40 minutes, every second counts, making a structured approach essential. Aspirants who combine smart set selection, regular practice, and analytical thinking often outperform those who rely solely on speed.
Before attempting any set, quickly scan all five to six sets in the section. Identify the sets that appear most familiar or less calculation-heavy. This ensures you secure marks quickly and don’t waste time on overly complex questions.
Divide your 40-minute window judiciously. Spend roughly 2–3 minutes per question initially and use a stop-loss strategy—if a set consumes too much time, move on and return later if time permits.
In DI, not every calculation requires full precision. Ratios, percentages, differences, and estimation techniques can save crucial minutes, especially in bar graphs, line charts, or pie charts.
For LR puzzles, create clear visual representations. Grids, tables, charts, and diagrams reduce cognitive load and prevent repeated errors. Stepwise deduction ensures logical consistency and speeds up reasoning.
Focus on both speed and accuracy. Track patterns sets that appear frequently can be prioritised, and uncommon ones can be handled with flexible strategies.
Post-mock analysis is where real improvement happens. Identify recurring errors, time-draining question types, and weak topics. Adjust your strategy accordingly, rather than blindly practising more questions.
The DILR section tests not only reasoning ability but also speed and accuracy under pressure. Regular practice of timed sets helps build confidence, maintain concentration, and avoid panic during tricky or lengthy puzzles.
Boost your CAT 2025 preparation with Careers360’s specially designed DILR ebooks. These resources cover all question types, including logical reasoning and data interpretation, with detailed solutions and strategies. Optimised for CAT exam 2025 aspirants, the ebooks help improve speed, accuracy, and problem-solving skills, making them essential for scoring high in the DILR section.
CAT DILR eBook Title | Download Links |
CAT 2025 Mastery: Chapter-wise MCQs for Success for VARC, DILR, Quant | |
Ultimate DILR CAT 2025 Guide: Concepts, Practice Sets and Detailed Solutions | Download Now |
Mastering CAT Exam: VARC, DILR, and Quant MCQs & Weightages | |
CAT DILR Questions with Solution, Download LRDI Questions for CAT |
Frequently Asked Questions (FAQs)
The DILR section typically includes 20 questions divided into four sets, with each set containing 4–6 questions. The section duration is 40 minutes, and it is common to have a mix of Data Interpretation (DI) and Logical Reasoning (LR) questions.
Start by scanning all four sets in the first 3–4 minutes. Choose sets where data looks structured (like tables or bar charts) and conditions are clear. Avoid time traps with long narratives or too many conditional clues, accuracy and smart selection matter more than solving all sets.
Yes, an on-screen calculator is available during the exam. However, heavy dependency on it slows you down. It’s best used for verifying ratios or percentages. Practice mental approximation during mock tests to improve both speed and confidence.
Begin with individual question types, DI charts, logical puzzles, and Venn sets, before moving to full-length mixed sets. Daily timed practice, analysis of mock tests, and solving previous CAT DILR sets (2017–2023) are crucial for pattern recognition and time optimisation.
Each correct answer gives +3 marks and each wrong answer incurs −1 mark (for MCQs). Non-MCQs have no negative marking. Scoring 30–35 marks typically places a candidate above the 95th percentile, depending on difficulty level up.
Important Data Interpretation (DI) topics include tables, bar and pie charts, line graphs, and caselets. Key Logical Reasoning (LR) areas cover seating arrangements, puzzles, blood relations, directions, syllogisms, and scheduling problems.
The CAT 2025 DILR section includes 22 questions across five sets, with 40 minutes to complete. It tests your ability to interpret data quickly and apply logical reasoning to solve complex problems under time pressure.
Scan all sets at the start and attempt the easiest or most familiar ones first. Skip time-consuming sets initially and return to them later. It ensures you maximise accuracy while managing your 40-minute window efficiently.
Yes, you should and picking the right set is important. Attempt easy and moderate ones first to maximise your score.
Start by solving previous years’ CAT papers, practice different types of sets daily, and focus on speed as well as accuracy.
On Question asked by student community
Hello,
With 802 marks in TS Inter and ST category, you have a fair chance of getting admission in BPT (Bachelor of Physiotherapy) in some private colleges through state counselling.
However, for government colleges, the cutoff may be slightly higher, so keep options open for management quota or allied health colleges too.
Hope you understand.
Hey,
You already have a strong profile with the score of 58% in Class 10, 74% in Class 12, and 80% in graduation, but admission in IIT Bombay, Shailesh J Mehta School of Management is quite competitive, especially if you are in general category because the cutoff for general goes to 98.5-99%. Your CAT percentage is impressive but your 10th marks might reduce your score during the shortlisting process. If you perform well in Written Ability Test and Personal Interview, and present your commerce background you still stand a fair chance. But it would also be wise if you have some backups like MDI Gurugram, IMT Ghaziabad, IMI Delhi, where your marks and profile will fit well in their selection range.
HELLO,
I am providing you the link below through which you will be able to download the previous 10 years CAT question papers
Here is the link :- CAT Previous year Question papers
Hope this Helps!
The three key formulas that can solve almost all Profit & Loss problems are:
Profit/Loss % = (Profit or Loss / Cost Price) × 100%, where CP is the cost price.
Discount % = (Discount / Marked Price) × 100%, where MP is the marked price.
Mark up % = (Mark up Value / Cost Price) × 100%, where CP is the cost price.
These formulas can be adapted for problems involving discounts, marked price, or successive gains/losses.
For detailed examples and variations, you can from the article
Hello,
Yes, Pragati Engineering College offers seats in Category-B (Management quota) for B.Tech programmes. The selection criteria is mentioned as the per the guidelines issued by the AP State Council of Higher Education (APSCHE). The applications are available on the college's official website.
You can know more about the college and the courses from the link given below:
https://www.careers360.com/colleges/pragati-engineering-college-surampalem
Hope it helps!!!
Directions for question :
M/s Deloitte Touche Tohmatsu Limited, one of the top four audit and accounting firms in the world with headquarters at London, UK, and with an operational presence in 153 countries, hires Management Trainees (MT) from all the premier management institutes of India thrice every year, in the months of January, May and September.
Each new group of Management Trainees (MT) have to go through a four month rigorous training schedule, after which they have to pass through a test consisting of a written assessment and a case-analysis. The top hundred ranked Management Trainees (MT) based on the performance in the test are confirmed as Management Executives (ME). The rest are given the opportunity of undergoing the training for four months one more time along with the next batch of Management Trainees (MT) and then passing through the subsequent test consisting of the written assessment and case-analysis. The Management Trainee (MT) who fails to get confirmed as a Management Executive (ME) the second time is fired.
The scatter-graph below depicts the number of Management Trainees (MT) at Deloitte taking the tests from January 2020 till May 2022, and the vis-à-vis hired Management Trainees (MT) at Deloitte who were fired :
It is also known that for the month of September 2019 at Deloitte, 96 hired Management Trainees (MT) failed to be confirmed as a Management Executive (ME) the first time, and that 36 hired Management Trainees (MT) were fired.
Question :
In which test did the minimum number of Management Trainees (MT) get confirmed as a Management Executive (ME) in the second attempt ?
September 2020
May 2021
January 2021
January 2022
Directions for question:
The bar-graph given below shows the foreign exchange reserves of Nepal (in million Rupees) from 2014 to 2021. Answer the following questions based on the graph :
Question:
What was the percentage increase (rounded to the nearest integer, if deemed necessary) in the foreign exchange reserves in 2020 over 2016 ?
Admissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
Ranked Under 100 B-Schools in India by NIRF | AACSB Member | AICTE Approved | Highest CTC 26 LPA | Average CTC of the Top 25% Students is 13 LPA
Ranked No. 3 Business School in India and no.35 in world by Financial Times MiM 2025 Ranking | Highest CTC: INR 89 LPA
AMBA & BGA ACCREDITED | Top Recruiters-Microsoft, Bain, HSBC, Deloitte, Barclays and many more
IBSAT 2025-Your gateway to MBA/PGPM @ IBS Hyderabad and 8 other IBS campuses | Scholarships worth 10 CR
1 Exam accepted by 17 Top Symbiosis Institutes for 29 MBA programmes.
