CAT 2025 Formula Sheet PDF: All Important Quantitative Aptitude Formulas for Quick Revision

Key Features of the CAT 2025 Formula Sheet

The CAT 2025 Formula Sheet is a strategic resource designed to help aspirants quickly revise and recall essential formulas across key topics like Arithmetic, Algebra, Geometry, and Trigonometry. It enhances exam preparation by offering structured, topic-wise Quantitative Aptitude formulas that improve problem-solving efficiency and accuracy during the CAT exam. This sheet consists of important formulas that candidates require during CAT 2025 preparation, ensuring students have everything they need in one place.

1. Topic-Wise Segregation for Focused Preparation

The CAT 2025 Formula Sheet is systematically divided into core Quantitative Aptitude topics such as Arithmetic, Algebra, Geometry, Trigonometry, and Number System. This organised structure helps aspirants target specific areas during revision. The clear division of important formulas for CAT preparation makes it easier to build accuracy step by step.

2. Comprehensive and Exam-Relevant Formulas

It includes all important formulas for CAT quant that are frequently tested in past exams. Only high-utility formulas that directly aid in solving Quant questions are included. By providing a selective formulas list for the CAT exam, it helps students avoid distractions and concentrate on formulas with the highest exam relevance and scoring potential.

3. High-Visibility Layout for Quick Recall

Designed with readability in mind, the sheet uses bold headings, colour-coded sections, and concise formats to make it visually appealing and easy to scan. Since important formulas for CAT preparation need to be revised multiple times, this format makes it highly effective for complete CAT 2025 revision, especially when quick recall is essential.

4. Quick Revision-Friendly Format

Ideal for daily practice and mock test preparation, the formula sheet allows aspirants to revise all crucial formulas quickly. It is also useful for learning shortcuts and tricks for CAT quant that save time in the exam. For serious aspirants, having the important formulas for CAT preparation ready helps in mastering speed-based problem-solving techniques required for the Quantitative Aptitude section.

5. Updated According to the Latest CAT Exam Pattern

The formula sheet is regularly updated based on the latest trends, question formats, and difficulty levels observed in recent CAT exams. This ensures that aspirants are not only revising the right formulas but also staying aligned with the current CAT 2025 exam syllabus. By consistently practising the must-know formulas for CAT 2025, students can boost confidence and accuracy.

CAT Important Formulas of Geometry

Mastering important geometry formulas is crucial for cracking the CAT exam, as geometry is a key topic in the Quantitative Aptitude section. The following section covers all essential CAT geometry formulas, including areas, polygons, angles, and properties of triangles and circles to help you solve problems quickly and accurately.

CAT Important Formulas of Trigonometry

Trigonometry plays a vital role in the CAT Quantitative Aptitude section, making it essential to learn and memorise key formulas. This comprehensive list of important CAT trigonometry formulas helps aspirants solve complex problems with speed, accuracy, and confidence during the exam.

1. Basic Trigonometric Ratios

These are defined in relation to a right-angled triangle:

$\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}$

$\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}$

$\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}$

$\csc \theta = \frac{\text{Hypotenuse}}{\text{Opposite side}}$

$\sec \theta = \frac{\text{Hypotenuse}}{\text{Adjacent side}}$

$\cot \theta = \frac{\text{Adjacent side}}{\text{Opposite side}}$

2. Pythagorean Identities

$\sin^2 \theta + \cos^2 \theta = 1$

$1 + \tan^2 \theta = \sec^2 \theta$

$1 + \cot^2 \theta = \csc^2 \theta$

3. Trigonometric Functions of Negative Angles

$\sin(-\theta) = -\sin \theta$

$\cos(-\theta) = \cos \theta$

$\tan(-\theta) = -\tan \theta$

$\csc(-\theta) = -\csc \theta$

$\sec(-\theta) = \sec \theta$

$\cot(-\theta) = -\cot \theta$

4. Angle Sum and Difference Formulas

$\sin(A + B) = \sin A \cos B + \cos A \sin B$

$\sin(A - B) = \sin A \cos B - \cos A \sin B$

$\cos(A + B) = \cos A \cos B - \sin A \sin B$

$\cos(A - B) = \cos A \cos B + \sin A \sin B$

$\tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}$

$\tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B}$

Quantitative Aptitude Formulae for CAT 2025

Quantitative Aptitude formulas form the foundation of the Quantitative Aptitude section in the CAT 2025 exam. Here are some important CAT 2025 quant section-wise formulae for CAT 2025 preparation:

Arithmetic

The Arithmetic section is the most important section in the Quantitative Aptitude Section, which is also useful to solve the Data Interpretation problems. Following are some 50+ Important Formulas for CAT Preparation of this section which are given in this CAT Formula Sheet:

Percentage

Following are some Important CAT Formulas of percentage:

$X \text{ is what percentage of } Y = \frac{X}{Y} \times 100$

$X \text{ is what percentage more/less than } Y = \frac{|X - Y|}{Y} \times 100$

Shortcut Formulas

Following are some formulas which can be used as CAT Quant Formulae:

Profit & Loss:

Following are some Important CAT Formulas of this topic:

Simple Interest (S.I.) & Compound Interest (C.I.):

Following are some basic and Important Formulas for CAT 2025 related to Simple Interest and Compound Interest:

Shortcut Formulas

Following are some formulas which can be used as CAT Quant Formula Cheat Sheet for the preparation and exam point of view:

Time, Speed & Distance:

Following are some basic and Important Formulas for CAT 2025 related to Time, Speed and Distance:

Trains:

Boat & Streams:

Clocks

Shortcut Formulas

Following are some Quantitative Aptitude Formulas which can be used as a CAT Quant Formula Cheat Sheet for the preparation and exam point of view:

If the distance covered in each stage of the journey is the same, but speeds are different, then the average speed is the harmonic mean of the different speeds.

Ex: If distance between point A to B and B to C are same and are covered with the speed of $s_1$ and $s_2$ respectively. Then-

Average Speed $= \dfrac{2s_1s_2}{s_1+s_2}$

If the time taken in each stage of journey is same, but speeds are different, then the average speed is the average of the different speeds.

Ex: If time taken between points A to B and B to C is same and these distances are covered with the speed of $s_1$ and $s_2$ respectively. Then-

Average Speed $= \dfrac{s_1+s_2}{2}$

If two people start running on a circular track of length $D$ km in the same direction from the same point with speeds $a$ & $b$ kmph, then-

(i) Time taken in first meeting $= \dfrac{D}{|a-b|}$ hr

(ii) Time taken to meet again at the starting point $= \text{LCM}\left(\dfrac{D}{a}, \dfrac{D}{b}\right)$ hr

(iii) Number of distinct meeting points $= |x-y|$

$\{x \ \& \ y \ \text{are the simplified ratio of speeds, e.g. If speeds } a \ \& \ b \ \text{ are 12 kmph \& 9 kmph respectively, then } x:y=12:9=4:3; \ \text{So, } x=4, y=3\}$

If two people start running on a circular track of length $D$ km in the opposite direction from the same point with speeds $a$ & $b$ kmph, then-

(i) Time taken in first meeting $= \dfrac{D}{a+b}$ hr

(ii) Time taken to meet again at the starting point $= \text{LCM}\left(\dfrac{D}{a}, \dfrac{D}{b}\right)$ hr

(iii) Number of distinct meeting points $= |x+y|$

$\{x \ \& \ y \ \text{are the simplified ratio of speeds}\}$

If a person $P$ starts from $A$ and heads towards $B$ and another person $Q$ starts from $B$ and heads towards $A$ and they meet after a time $t$ then,

$t = x \cdot y$

$[\text{where } x = \text{time taken (after meeting) by P to reach B and } y = \text{time taken (after meeting) by Q to reach A}]$

If the speed of the boat downstream is $u$ kmph and the speed of the boat upstream is $v$ kmph, then-

Speed of the boat in still water $= \dfrac{u+v}{2}$ kmph

Rate of stream $= \dfrac{u-v}{2}$ kmph

Geometry

The Geometry section is the lengthiest section in the Quantitative Aptitude Section which has lots of properties and formulas. Following are 50+ Important Formulas for CAT Preparation of this section which are given in this CAT Formula Sheet:

1. Triangles:

Properties of Triangles:

The sum of all interior angles in a triangle is $180^\circ$ and the sum of all exterior angles is $360^\circ$.

The sum of any two sides is always greater than the third one and the difference of any two sides is less than the third one.

Let $a, b, c$ be the sides of a triangle, then

$|b-c| < a < b+c$

In a scalene triangle the greatest side is always greater than one-third of the perimeter and less than half of the perimeter.

Let $a, b, c$ be the sides of the triangle and $a$ be the greatest side. Let the perimeter be $P$. Then

$\dfrac{P}{3} < a < \dfrac{P}{2}$

Example: In a scalene triangle $ABC$, the perimeter is $24$ cm and all sides are integers.

Let $a, b, c$ be sides of the triangle with $a$ the greatest side. Then

$\dfrac{24}{3} < a < \dfrac{24}{2}$

$8 < a < 12$

So possible values are $9, 10, 11$ cm.

For $a, b, c$ sides of a triangle and $a$ the greatest side:

If $a^2 < b^2 + c^2$, then the triangle is acute angled.

If $a^2 = b^2 + c^2$, then the triangle is right angled (Pythagoras theorem).

If $a^2 > b^2 + c^2$, then the triangle is obtuse angled.

(Here $D$ is the midpoint of side $AC$, so $AD = DC$)

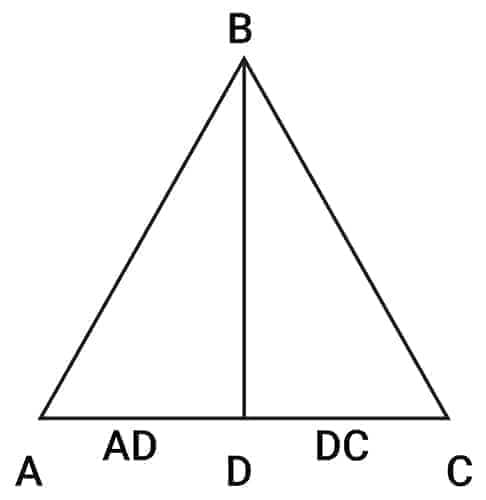
Midpoint of triangle

• Length of the Median –
  BD=122(AB2+BC2)−AC2

• 3× (Sum of squares of sides) =4× (Sum of squares of medians), that is,
  3(a2+b2+c2)=4(Ma2+Mb2+Mc2)
  where a,b,c are the sides of the triangle and Ma,Mb,Mc are the medians.

• In a right-angled triangle, Median of Hypotenuse =Hypotenuse2
  That is,
  CD=AB2

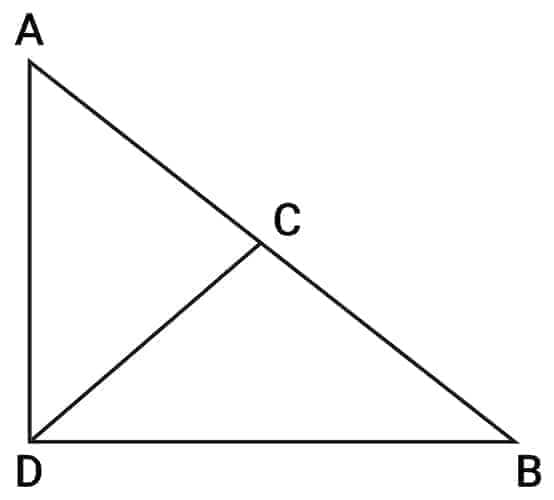
Median of hypotenuse

If all the medians are drawn in the triangle, then the 6 small triangles are generated in the triangle, which are equal in the Area.

Area of Triangle:

Heron’s Formula

If all sides of a triangle are given. Let $a, b, c$ be the sides of the triangle –

Area $= \sqrt{s(s-a)(s-b)(s-c)}$ where $s = \dfrac{a+b+c}{2}$ is the semiperimeter.

If two sides and the included angle are given –

Area $= \dfrac{1}{2} \times \text{(Product of given sides)} \times \sin(\text{included angle})$

Area $= \dfrac{1}{2} \times a \times b \times \sin C$

(Example: sides $a, b$ and included angle $C$ are given)

If a side and its respective altitude (perpendicular drawn from the opposite vertex) is given, then –

Area of the triangle $= \dfrac{1}{2} \times \text{Base} \times \text{Height (Altitude)}$

Shortcut Formulas

Area of an equilateral triangle = $ \frac{\sqrt{3}}{4} a^2 $

Height (Altitude) of an equilateral triangle = $ \frac{\sqrt{3}}{2} a $

Area of a triangle = $ r \times s $ (where $r$ is the inradius and $s$ is the semiperimeter)

Area of a triangle = $ \frac{abc}{4R} $ (where $a$, $b$, $c$ are sides and $R$ is the circumradius)

Quadrilaterals:

3. Circle:

Circumference of a circle $= 2\pi r$

Area of a circle $= \pi r^2$

For a semi-circle:

Circumference of a semi-circle $= \pi r$

Perimeter of a semi-circle $= \pi r + 2r$

Area of a semi-circle $= \dfrac{\pi r^2}{2}$

Sector & Segment of circle

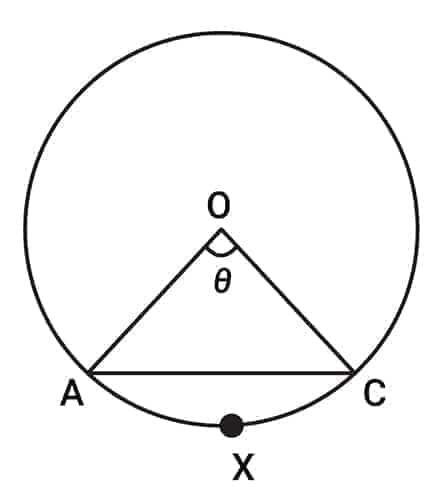
$OAXC$ is called the sector of the circle and $AXC$ is called the segment.

Length of arc $AXC = \dfrac{\theta}{360} \times 2\pi r$ (where $r$ is the radius)

Area of sector $OAXC = \dfrac{\theta}{360} \times \pi r^2$

$2 \times \text{Area of sector} = \text{Length of arc} \times \text{Radius}$

Area of segment $AXC = \text{Area of sector } OAXC - \text{Area of } \triangle OAC$

$A = \dfrac{\theta}{360} \pi r^2 - \dfrac{1}{2} r^2 \sin \theta$

Where:

$\theta$ = angle subtended at the center (in degrees)

$r$ = radius of the circle

Common Tangent

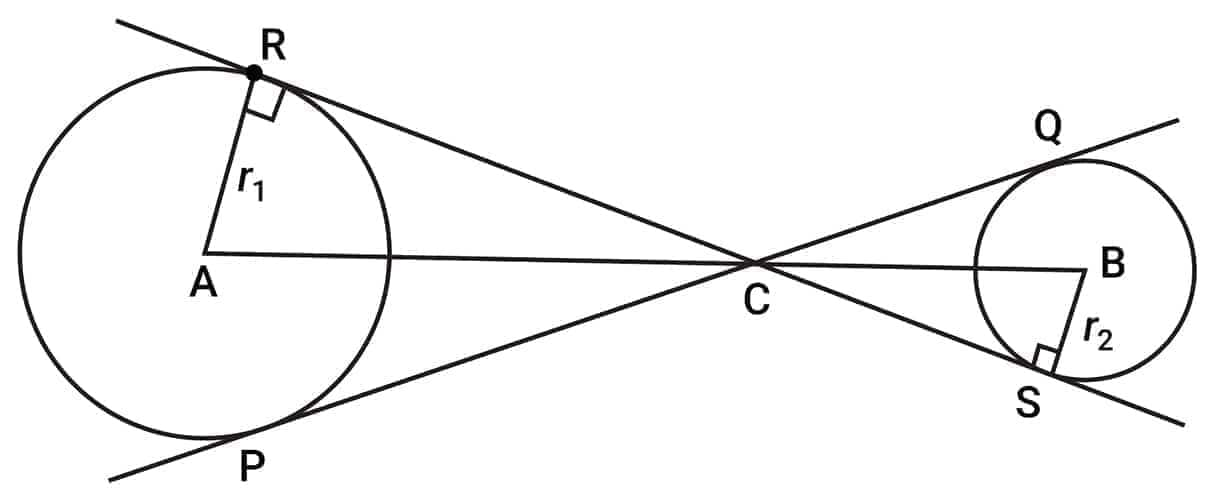
$PQ$ and $RS$ are the direct common tangents of the circles, which are equal in length.

Length of direct common tangent $(L)$:

$L^2 = d^2 - (r_1 - r_2)^2$

Where:

$d =$ distance between centers of the circles

$r_1, r_2 =$ radii of the circles

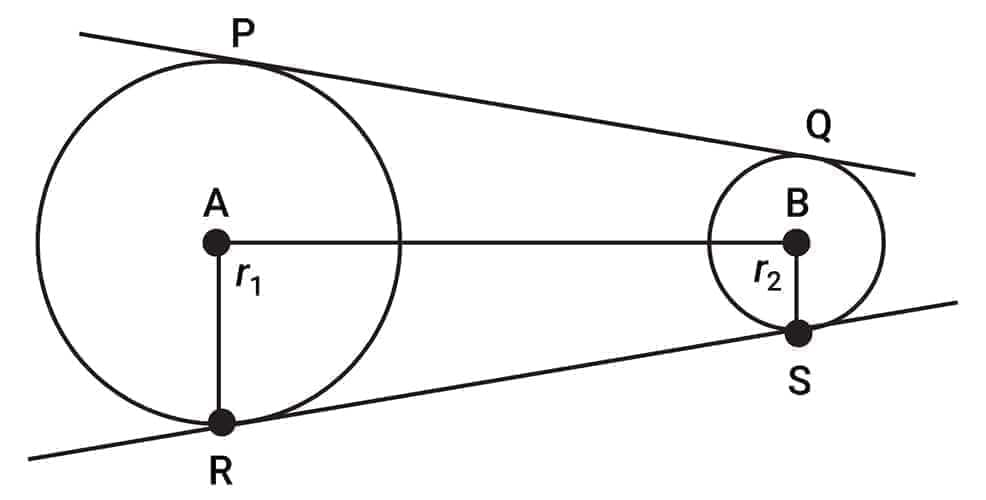
$PQ$ and $RS$ are the transverse common tangents of the circles, which are equal in length.

Length of transverse common tangent $(L)$:

$L^2 = d^2 - (r_1 + r_2)^2$

Where:

$L =$ length of the transverse common tangent

$d =$ distance between the centers of the two circles

$r_1, r_2 =$ radii of the two circles

Mensuration:

Algebra

The Algebra section is a critical part of the Quantitative Aptitude section in the CAT exam. Below are over 50 important formulas for CAT preparation in this section, which are provided in this comprehensive CAT Formula Sheet:

1. Quadratic Equations

General quadratic equation will be in the form of $ax^2 + bx + c = 0$

Values of $x$ which satisfy the equation are called the roots of the equation. To find the roots, Shreedhara Acharya's Formula is used.

Roots of the equation: $x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Sum of the roots $= -\dfrac{b}{a}$

Product of the roots $= \dfrac{c}{a}$

Difference of the roots $= D$, where $D = b^2 - 4ac$

If $D > 0$, then the roots are real and distinct.

i. If $D$ is a perfect square, then roots are rational (e.g. $x = 1, 6$)

ii. If $D$ is not a perfect square, then roots are irrational or conjugate surds (e.g. $x = 3 - \sqrt{5}, \ 3 + \sqrt{5}$)

If $D = 0$, then the roots are real and equal.

If $D < 0$, then the roots are imaginary and distinct.

For $y = ax^2 + bx + c$, where $a > 0$:

Minimum value occurs at $x = -\dfrac{b}{2a}$ and is given by

$y = -\dfrac{D}{4a}$ (Minimum value)

For $y = ax^2 + bx + c$, where $a < 0$:

Maximum value occurs at $x = -\dfrac{b}{2a}$ and is given by

$y = -\dfrac{D}{4a}$ (Maximum value)

Where $D = b^2 - 4ac$ is the discriminant.

If the roots of the quadratic equation are $a$ and $b$, then the quadratic equation is:

$x^2 - Sx + P = 0$, where $S = a + b$ and $P = ab$

That is, $x^2 - (a+b)x + ab = 0$

Progression & Series

Arithmetic Progression (A.P.)

If a is the first term and d is the common difference then the Arithmetic Progression (A.P.). can be written as-

• a, a+d, a+2d, a+3d, …

Let $a =$ first term

$d =$ common difference

$n$ = number of terms

Nth term of the A.P. –

$T_n = a + (n-1)d$

Sum of the first $n$ terms of the A.P. $(S_n)$ = Average of all the terms $\times$ number of terms $(n)$.

The average of the terms can be found easily:

If the number of terms is odd, then the middle term will be the average.

Example: $2, 5, 8, 11, 14$ are terms of the A.P., then the middle term $8$ is the average.

So, $S_n = \text{average} \times n = 8 \times 5 = 40$.

If the number of terms is even, then the average of the middle two terms will be the average of the A.P.

Formula for sum of $n$ terms:

$S_n = \dfrac{n}{2} \big[ 2a + (n-1)d \big]$

Shortcut Formulae

$S_n = \dfrac{n}{2}(a+l)$ (where $a =$ first term, $l =$ last term, $n =$ number of terms)

$n = \dfrac{l-a}{d}+1$ (number of terms in A.P.)

Geometric Progression (G.P.)

If $a$ is the first term and $r$ is the common ratio, then the G.P. can be written as: $a, ar, ar^2, ar^3, \dots$

Nth term of the G.P.: $T_n = a \cdot r^{n-1}$

Sum of the first $n$ terms:

If $|r| < 1$: $S_n = a \cdot \dfrac{1-r^n}{1-r}$

If $r > 1$: $S_n = a \cdot \dfrac{r^n-1}{r-1}$

Sum of infinite terms of the G.P. (if $|r|<1$): $S_\infty = \dfrac{a}{1-r}$

Where: $a =$ first term, $r =$ common ratio, $n =$ number of terms

$|r|<1$ ensures the series converges.

Shortcut Formulas

If there are odd no. of terms in a G.P., then the product of all terms are equal to the nth power of the middle term.

e.g. 2,6,18,54,162 are the terms of a G.P.

Then the products of all the terms = 185

Harmonic Progression (H.P.)

If a,b,c are in A.P., then $\frac{1}{a},\frac{1}{b},\frac{1}{c}$ are in Harmonic Progression (H.P.).

n-th term of the H.P.=$\frac{1}{n}$-th term of the corresponding A.P.

Series

Sum of first $n$ natural numbers: $1+2+3+\cdots+n = \dfrac{n(n+1)}{2}$

Sum of squares of first $n$ natural numbers: $1^2+2^2+3^2+\cdots+n^2 = \dfrac{n(n+1)(2n+1)}{6}$

Sum of cubes of first $n$ natural numbers: $1^3+2^3+3^3+\cdots+n^3 = \left(\dfrac{n(n+1)}{2}\right)^2$

Sum of first $n$ natural odd numbers: $1+3+5+\cdots+(2n-1) = n^2$

Sum of squares of first $n$ even numbers: $2^2+4^2+6^2+\cdots+(2n)^2 = \dfrac{2n(n+1)(2n+1)}{3}$

Sum of squares of first $n$ odd numbers: $1^2+3^2+5^2+\cdots+(2n-1)^2 = \dfrac{n(2n+1)(2n-1)}{3}$

Indices & Surds

Product Rule: $a^m \cdot a^n = a^{m+n}$

Quotient Rule: $\dfrac{a^m}{a^n} = a^{m-n}$

Power of a Power: $(a^m)^n = a^{mn}$

Power of a Product: $(ab)^n = a^n \cdot b^n$

Power of a Quotient: $\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}$

Negative Exponent: $a^{-n} = \dfrac{1}{a^n}$

Shortcut Formulae

Infinite Product: $\prod_{n=1}^{\infty} a_n = \lim_{n \to \infty} \prod_{k=1}^{n} a_k$

Logarithmic Rules and Properties

Definition of Logarithm: $\log_b a = x \;\;\Longleftrightarrow\;\; b^x = a$

Log of 1: $\log_b 1 = 0 \;\; (b>0, \; b \neq 1)$

Log of the base itself: $\log_b b = 1$

Log of a product: $\log_b(mn) = \log_b m + \log_b n$

Log of a quotient: $\log_b \left(\dfrac{m}{n}\right) = \log_b m - \log_b n$

Log of a power: $\log_b(m^n) = n \cdot \log_b m$

Change of base formula: $\log_b a = \dfrac{\log_k a}{\log_k b}$

Base switch rule: $\log_a b = \dfrac{1}{\log_b a}$

Why is the CAT 2025 Formulae Important?

CAT 2025 Formulae is crucial for MBA exam preparation as it compiles important formulas for CAT preparation and concepts, streamlining study efforts and enhancing exam readiness. This resource not only aids in quick recall but also fosters a deeper understanding of quantitative topics.

• A consolidated CAT math formulas PDF allows for focused study sessions. It also reduces the time spent searching for formulas across various resources. For aspirants, keeping a formula list for CAT exam in one place ensures efficiency in revision.

• Regular use of the CAT formula PDF helps in developing quick problem-solving techniques. This is essential for tackling the time constraints of the exam. By practising with shortcuts and tricks for CAT quant, candidates can improve both speed and accuracy.

• The formula sheet highlights the important formulas for CAT 2025, making last-minute revision easier. It ensures that students cover all must-know formulas for CAT 2025 without missing high-priority areas.

• Familiarity with formulas leads to fewer mistakes during the test. This boosts both confidence and accuracy. Understanding which important formulas for CAT preparation are most relevant helps aspirants attempt strategically and maximise their scores.

How to Memorise Formulas for CAT Effectively

Learning important formulas for CAT preparation requires more than memorisation; it needs a strategy that blends practice with smart revision. Grouping important formulas for CAT preparation by topics like Arithmetic, Algebra, Geometry, and Trigonometry makes recall systematic and avoids confusion during the exam.

• Maintaining a dedicated notebook of important formulas for CAT preparation helps in quick revisions and also works as a personalised formulas list for CAT exam. Writing each formula with an example ensures you understand both its structure and application.

• Visual resources play a key role in remembering important formulas for CAT preparation, especially in Geometry and Trigonometry. Linking concepts with diagrams or mnemonics makes retention effortless and aligns with shortcuts and tricks for CAT quant.

• Consistent revision of important formulas for CAT preparation is vital. Turning your notes into a cat math formulas pdf allows you to revise on the go and keeps all essential content in one place.

• Lastly, solving practice questions using important formulas for CAT preparation reinforces memory and accuracy. This habit builds confidence and ensures you master the must-know formulas for CAT 2025 well before the exam.

Commonly Forgotten CAT Formulas You Must Revise

Many aspirants struggle because they overlook important formulas for CAT preparation that appear frequently in the exam. Simple percentage and ratio formulas, though basic, remain part of important formulas for CAT preparation and are often forgotten under time pressure.

• Geometry concepts like areas of circles, triangles, and polygons are key important formulas for CAT preparation that must be revised repeatedly, as skipping them can cost valuable marks. Similarly, algebraic identities such as (a+b)2(a+b)^2(a+b)2 and (a−b)2(a-b)^2(a−b)2 fall under important formulas for CAT Quant and often slip from memory if not revised consistently.

• In Quant, trigonometric ratios and identities are also important formulas for CAT preparation that aspirants tend to ignore, even though they frequently appear in questions. Keeping these in a formulas list for CAT exam helps minimise errors.

• The Number System contains divisibility rules and LCM-HCF shortcuts, both part of important formulas for CAT preparation, that students overlook while focusing on advanced topics. Converting them into a quick CAT math formulas PDF ensures they are revised regularly.

CAT Formula Applications in Previous Year Questions

Understanding the real use of important formulas for CAT preparation in previous year questions helps aspirants apply concepts accurately under exam conditions. Many questions rely on simple, important formulas for cat quant from Arithmetic, like percentages, profit-loss, and ratio-proportion, which appear repeatedly across years.

Geometry problems in past CAT papers often test important formulas for CAT 2025 involving triangles, circles, and polygons. Practising these helps students quickly recall relevant formulas during the exam. Similarly, algebraic expressions and identities are part of important formulas for CAT preparation that regularly appear in Quant questions, reinforcing the need for consistent revision.

Trigonometry and mensuration questions also use important formulas for CAT preparation, where knowing shortcuts can save precious time. Maintaining a CAT math formulas PDF or a formulas list for CAT exam ensures aspirants can revise these efficiently before attempting mocks.

Even Data Interpretation sets occasionally require important formulas for CAT preparation, such as averages, percentages, and ratios, to solve tables and charts accurately. Analysing previous years’ patterns helps aspirants identify which must-know formulas for CAT 2025 carry the highest weight, enhancing preparation strategy.

CAT Formula Shortcuts vs Detailed Methods: Which is Best?

When preparing for CAT, students often face one big question: Should I learn shortcuts or follow detailed methods? Both have their own value. Shortcuts save time, while detailed methods build strong basics. To do well in CAT 2025, you must balance both and use them wisely.

Shortcuts in CAT formulas

Shortcuts are quick tricks or smart steps that help you solve problems faster. For example, using direct percentage conversion instead of step-by-step calculation. In the CAT exam, where time is limited, shortcuts can increase speed and help you attempt more questions.

Detailed methods in CAT formulas

Detailed methods mean solving step by step with full logic. This approach is useful when a question is tricky or when you are not sure about the shortcut. Detailed solving also builds strong fundamentals in topics like Algebra, Geometry, and Arithmetic. Without strong basics, shortcuts may confuse you.

How to Remember CAT Formulas for Long Time

Remembering CAT formulas for a long time is one of the biggest challenges for students. There are hundreds of formulas in Quantitative Aptitude, Algebra, Geometry, Arithmetic, and Modern Math. If you only read them once, you may forget them during the exam. To prepare well for CAT 2025, you need simple tricks that help you keep formulas in memory for months.

Revise daily in short time

Spend 10–15 minutes every day with your formula sheet. Daily revision keeps formulas fresh in your mind. It is better to revise for a short time every day than to spend two hours once a week. Small, regular practice makes your memory stronger and helps you recall quickly during the CAT exam.

Write and solve questions

Do not only read the formula. Write it down on paper and solve one or two questions based on it. When you write and solve, your brain builds a stronger memory. For example, if you learn the formula for Compound Interest, solve a small sum immediately. Practice helps you remember for a long time.

Use flashcards or small notes

Make small cards or sticky notes with one formula on each. Carry them in your bag or keep them near your study table. Look at them whenever you get free time. You can also use apps like Anki or Quizlet for digital flashcards. Flashcards give you quick revision and help you recall anytime, anywhere.

Link formulas with examples

Always connect formulas with simple real-life examples. For example, link the “Area of Circle = πr²” with the shape of a pizza. Or connect “Speed = Distance/Time” with your daily travel. When your brain sees a real example, it remembers the formula for a long time.

Teach or say aloud

Explain the formula to a friend or say it aloud to yourself. Teaching is one of the best ways to remember. When you speak the formula and explain how it works, your brain stores it more strongly. This trick is very useful in CAT preparation.

Revise before sleep

Spend five minutes before sleeping to read some formulas. The brain works even during sleep and stores what you revise at night. This is why late-night revision is powerful. It makes sure that the formulas stay in your memory for many days.

Best Ways to Create CAT Formula Sheet

A CAT formula sheet helps students save time and avoid mistakes while solving questions. It keeps all important formulas in one place so that revision becomes fast and simple. By writing formulas topic-wise and keeping them short, clear, and easy to read, students can improve their speed and accuracy for CAT 2025 preparation.

Write topic by topic

Put all formulas under clear headings like Arithmetic, Algebra, Geometry, Numbers, and Modern Math. This makes revision simple. For example, keep all Percentage formulas in one place and all Geometry formulas in another. It saves time and avoids confusion.

Use notebook or digital file

You can note formulas in a notebook or type them in Google Docs or Word. A notebook is easy to carry, while a digital file is easy to edit. Pick the one that feels comfortable for your daily study.

Highlight important ones

Mark important formulas with colour pens or bold text. This makes them stand out on the page. When you revise, your eyes quickly move to the key formulas that are used more often in CAT questions.

Add diagrams for Geometry

Draw small figures like triangles, circles, or rectangles when you write Geometry formulas. Writing with diagrams makes the formula easy to remember. Visual memory helps you recall faster during problem-solving.

Make a one-page PDF

After collecting all formulas, create a single sheet with only the most important ones. Save it as a PDF or print it. This works well for last-minute revision before mock tests or the actual CAT exam.

Benefits of Keeping CAT 2025 Formula Sheet PDF

Keeping a CAT 2025 Formula Sheet PDF helps aspirants quickly revise key mathematical concepts, shortcuts, and important formulas for CAT preparation. It serves as a ready reference during preparation, saves time, and ensures nothing important is missed while solving quantitative and reasoning problems.

Quick access to all important formulas in one place

A CAT 2025 Formula Sheet brings all essential equations and shortcuts from Quantitative Aptitude and Data Interpretation together, allowing you to refer to them instantly without flipping through multiple books or notes. It complements a detailed formulas list for CAT exam and ensures you stay focused on high-utility concepts.

Saves revision time during last-minute preparation

With the exam approaching, time becomes critical. A ready-made CAT 2025 Formula Sheet cuts down on revision time by offering a focused list of important formulas for CAT preparation, helping you stay organised and stress-free. Aspirants can also pair this with a CAT math formulas PDF for quicker revisions.

Improves speed and accuracy in problem-solving

Frequent review of formulas boosts familiarity, which leads to quicker recall during the exam. This naturally improves your speed and reduces calculation errors in time-bound situations. Using shortcuts and tricks for CAT quant along with important formulas for CAT 2025 strengthens both accuracy and efficiency.

Reduces the risk of forgetting key concepts

Revisiting formulas regularly through a dedicated sheet helps reinforce memory. This ensures that vital concepts stay fresh, especially for topics you may not practise every day. Including must-know formulas for CAT 2025 in your revision ensures full coverage of scoring areas.

Helps identify formula-based shortcuts for tricky questions

Many CAT questions can be solved faster with the right shortcuts. A CAT 2025 Formula Sheet highlights these quicker methods, helping you attempt more questions efficiently within the limited time frame. Regularly reviewing the important formulas for CAT preparation ensures you know which techniques to apply during the test.