CAT QA Sample Questions - CAT Quantitative Aptitude Questions with Solutions

Quantitative Aptitude, or QA, is a section of the CAT exam that is feared by most, especially non-engineers. It consists of Arithmetic, Geometry, Number System, Algebra, and Modern Math. In this article, the candidates are presented with various important CAT QA Sample Questions with solutions so that they can gain an immediate understanding of the difficulty levels of the quantitative aptitude section of the CAT examination.

This Story also Contains

1. CAT QA Sample Questions for Practice
2. CAT QA Sample Questions with Solutions
3. CAT VARC Sample Questions
4. CAT DILR Sample Questions
5. Download Free Practice Questions with Detailed Solutions for CAT Quantitative Aptitude (QA) - MCQ PDFs

The difficulty level of QA in CAT exam 2023 was on the higher side, leading many to give up hope for a decent percentile. But if you understand all the chapters’ concepts properly, then you can tackle this section and clear the sectional cut-off with good marks. The candidates are encouraged to practice a lot of CAT Questions on Quantitative Aptitude to ensure that their preparation is on track.

CAT QA Sample Questions for Practice

Since only 40 minutes are given for the section, you must practice as many CAT quantitative aptitude questions as possible to understand how much time to allot to each question. You’ll also get to know your strengths and weaknesses by solving CAT QA sample questions. This way, you can focus on your weak areas and devote more time to understanding concepts.

CAT QA Sample Questions with Solutions

CAT Mixture and Allegation Questions

Question:
The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33 % and 17 %, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21 % then the volume, in cc, of the solution left in the second bottle is

(TITA)

Answer: 200cc

Using the allegation cross,

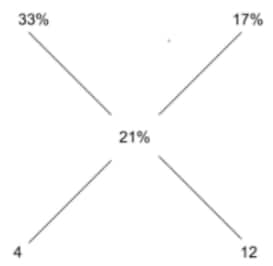
The two solutions are in the ratio of 1:3

Thus, 600cc of solution is added from the second bottle.

Thus, 800cc - 600cc = 200cc of the solution is remaining.

Hence, 200cc is the correct answer.

Question:

Amal buys 110 kg of syrup and 120 kg of juice, syrup being 20% less costly than juice, per kg. He sells 10 kg of syrup at 10% profit and 20 kg of juice at 20% profit. Mixing the remaining juice and syrup, Amal sells the mixture at 308.32 per kg and makes an overall profit of 64%. Then, Amal’s cost price for syrup, in rupees per kg, is

(TITA)

Answer: 160

Let the price of juice be Rs. x per kg.

Since the cost price of syrup is 20% less than the cost price of juice, the cost price of syrup is 0.8x per kg.

Total cost price of syrup = 110 0.8x = ₹88x

Total cost price of juice = 120 x = ₹120x

Total cost price = 88x + 120x = ₹208x

Since the overall profit percentage is 64%,

Total profit = 0.64(208x) = 133.12x

Profit generated on selling 10 kg of syrup which costs

₹0.8x per kg at 10% profit = 0.1 10 0.8x = 0.8x

Profit generated on selling 20 kg of juice which costs ₹x per kg at 20% profit = 0.2 20 x = 4x

The remaining profit (133.12x – (0.8x + 4x) = 128.32x) is generated by selling 100 kg of syrup and

100 kg of juice at ₹308.32 per kg.

The total selling price of 100 kg of syrup and 100 kg of juice is 200 308.32 = 2(30832)

Cost price of 100 kg of syrup = 0.8x 100 = ₹80x

Cost price of 100 kg of juice = x 100 = ₹100x

Total cost price = ₹80x + ₹100x = ₹180x

Profit = Selling price – Cost price

⇒ 128.32x = 2(30832) – 180x

⇒ 308.32x = 2(30832)

⇒ x = 200

Cost price of syrup per kg = 0.8 x = 0.8(200) = ₹160

CAT Percentages Questions

Question:

In the final examination, Bishnu scored 52% and Asha scored 64%. The marks obtained by Bishnu is 23 less, and that by Asha is 34 more than the marks obtained by Ramesh. The marks obtained by Geeta, who scored 84%, is

A. 357

B. 417

C. 439

D. 399

Answer: D

Let the total marks be T and scores of Bishnu, Asha and Ramesh be a, b and c respectively.

Given, a = 52% of T = c – 23 and b = 64% of T = c + 34

Hence, (60 – 52)% of T = (c + 34) – (c – 23) = 57

i.e., 12% of T = 57

hence, score of Geeta = 84% of T = 7 × 57 = 399

Question:

In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent 450 on rice in April, then how much did he spend on wheat in May?

A. Rs.560

B. Rs.570

C. Rs.590

D. Rs.580

Answer: A

Let John buy "m" kg of rice and "p" kg of wheat.

Now let the price of rice be "r" in April. Price in May will be "1.2(r)"

Now let the price of wheat be "w" in April. Price in April will be "1.12(w)".

Now he spent ₹150 more in May , so 0.2(rm) + 0.12(wp) = 150

It's also given that he had spent ₹450 on rice in April. So (rm) = 450

So 0.2(rm) = (0.2)(450) = 90 Substituting we get (wp) = 60/0.12 or (wp) = 500

Amount spent on wheat in May will be 1.12(500) = ₹560

Question:

In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to

A. 62

B. 55

C. 59

D. 66

Answer: D

Let the number of persons in the group be 100.

Then the people who are young = 28

Ans the number of literate persons = 65

Number of literates who are young = 25% of 65 = 16.25

Required answer

CAT Profit and Loss Questions

Question:

Anil, Bobby, and Chintu jointly invest in a business and agree to share the overall profit in proportion to their investments. Anil’s share of investment is 70%. His share of profit decreases by 420 if the overall profit goes down from 18% to 15%. Chintu’s share of profit increases by 80 if the overall profit goes up from 15% to 17%. The amount, in INR, invested by Bobby is

A. 2000

B. 2400

C. 2200

D. 1800

Answer: A

Let the total amount invested be ‘x’.

Given that, 70% of (18% of x – 15% of x) = 420

70% of 3% of x = 420

x = 20,000

Let Chintu’s share of investment be R%.

Thus, c% of 2% of 20,000 = 80

c = 20%

Thus, the amount invested by Bobby = 10% of 20,000 = ₹2000

Hence, option A is the correct answer.

CAT Number System Questions

Question:

How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?

(TITA)

Answer: 70

Let the numbers be of the form 100 a+10b+c, where a, b,and c represent single digits.

Then (100 c+10 b+a)-(100 a+10 b+c)=198

99c-99a=198

c-a=2.

Now, a can take the values 1-7. a cannot be zero as the initial number has 3 digits and cannot be 8 or 9 as then c would not be a single-digit number.

Thus, there can be 7 cases.

B can take the value of any digit from 0-9, as it does not affect the answer. Hence, the total cases will be 7×10=70.

Question:

How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7?

A. 42

B. 41

C. 40

D. 43

Answer: B

The number of multiples of 2 between 1 and 120 = 60

The number of multiples of 5 between 1 and 120 which are not multiples of 2 = 12

The number of multiples of 7 between 1 and 120 which are not multiples of 2 and 5 = 7

Hence, number of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7 = 120 - 60 - 12 - 7 = 41

CAT Algebra Questions

Question:

A donation box can receive only cheques of 100, 250, and 500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of 15250. Then, the maximum possible number of cheques of 500 that the donation box may have contained, is

(TITA)

Answer: 12

Let the number of cheques of ₹100, ₹250, and ₹500 be x, y, and z, respectively.

We need to find the maximum value of z.

x + y + z = 100 ...... (1)

100x + 250y + 500z = 15250

2x + 5y + 10z = 305 ...... (2)

Now multiply (1) by (2),

2x + 2y + 2z = 200 .......(3)

(2) - (3), we get:

3y + 8z = 105

At z = 12, x = 3

Therefore, the maximum value z can take is 12.

CAT Probability Questions

Question:

When a die is tossed twice, find the probability of getting a pair of numbers which has a sum of 8

A. 1/36

B. 2/36

C. 3/36

D. 5/36

Answer: D

A standard six-sided die has numbers from 1 to 6. To get a sum of 8, the possible combinations of two rolls that work are (2, 6), (3, 5), (4, 4), (5, 3), and (6, 2).

There are a total of 6 × 6 = 36 possible outcomes when you toss a die twice.

The probability of getting a sum of 8 is the number of successful outcomes (combinations that result in a sum of 8) divided by the total possible outcomes.

So, the probability is:

Number of successful outcomes = 5 (combinations: (2, 6), (3, 5), (4, 4), (5, 3), (6, 2))

Total possible outcomes = 36

Probability (P) = Number of Favorable Outcomes / Total Number of Possible Outcomes

Probability = 5/36

Question:

In a cricket match, a bowler bowls 48 balls, and the batsman hits boundaries 12 times. What is the probability that the batsman did not hit a boundary during these 48 balls?

A. 1/2

B. 3/4

C. 1/4

D. 2/3

Answer: B

First, calculate the probability of hitting a boundary (let's call it "H"), which is 12 out of 48 balls.

Probability of hitting a boundary (P(H)) = Number of boundaries / Total number of balls = 12/48

Now, to find the probability of not hitting a boundary (let's call it "N"), you can use the complement rule:

Probability of not hitting a boundary (P(N)) = 1 - Probability of hitting a boundary (P(H))

P(N) = 1 - P(H) = 1 - (12/48)

P(N) = 1 - (1/4)

P(N) = 4/4 - 1/4 = (4 - 1) / 4 = 3/4

So, the probability that the batsman did not hit a boundary during these 48 balls is 3/4.

CAT Geometry Questions

Question:

The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is

A. 3

B. 4

C. 6

D. 5

Answer: D

Sum of the three sides of a quadrilateral is greater than the fourth side.

Therefore, let the fourth side be

1 + 2 + 4 > d or d < 7

1 + 2 + d > 4 or d > 1

Possible values of d are 2, 3, 4, 5 and 6.

Question:

A trapezium ABCD has side AD parallel to BC, ∠BAD = 90°, BC = 3 cm and AD = 8 cm. If the perimeter of this trapezium is 36 cm, then its area, in sq. cm, is

(TITA)

Answer: 66

CAT Time, Speed, and Distance Questions

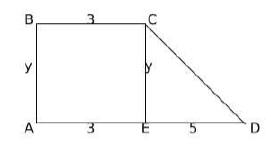
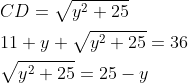
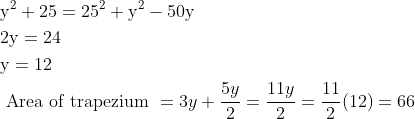
Question:

A and B are two railway stations 90 km apart. A train leaves A at 9:00 am, heading towards B at a speed of 40 km/hr. Another train leaves B at 10:30 am, heading towards A at a speed of 20 km/hr. The trains meet each other at

A. 11: 45 am

B. 11: 20 am

C. 11: 00 am

D. 10: 45 am

Answer: C

The distance travelled by A between 9:00 Am and 10:30 Am is 3/2 × 40 =60 km.

Now they are separated by 30 km

Let the time taken to meet =t

Distance travelled by A in time t + Distance travelled by B in time t = 30

40t + 20t =30 => t=1/2 hour

Hence they meet at 11:00 AM

CAT Simple and Compound Interest Questions

Question:

Nitu has an initial capital of 20,000. Out of this, she invests 8,000 at 5.5% in bank A, 5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in bank C alone, then her annual interest income, in rupees, would have been

A. 700

B. 800

C. 900

D. 1000

Answer: B

CAT Set Theory Questions

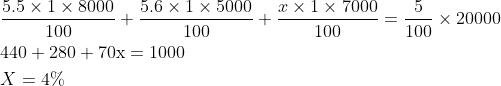
Question:

How many integers in the set {100, 101, 102,..., 999} have at least one digit repeated?

(TITA)

Answer: 252

Total number of numbers from 100 to 999 = 900

The number of three digits numbers with unique digits:

_ _ _

The hundredth's place can be filled in 9 ways (Number 0 cannot be selected)

Ten's place can be filled in 9 ways

One's place can be filled in 8 ways

Total number of numbers = 9×9×8 = 648

Number of integers in the set {100, 101, 102, ..., 999} have at least one digit repeated = 900 - 648 = 252

Question:

Which of the following sets is equivalent to set A = {a, b, c, d, e, f}?

A. B = {10, 5, 8, 21, 45, 78}

B. B = {c, a, b, f}

C. B = {–1, 0, 2, 4}

D. None of these

Answer: A

Equal sets are two sets that contain the same number of elements.

Here both the sets {a, b, c, d, e, f} and {10, 5, 8, 21, 45, 78} contain 6 elements and hence they are equivalent sets.

All other sets have 4 elements and hence they cannot be concluded as an equivalent set to {10, 5, 8, 21, 45, 78}

Hence, the correct answer is B = {10, 5, 8, 21, 45, 78}.

CAT Permutation and Combination Questions

Question:

How many three- digit numbers can be formed using digits {1, 2, 3, 4, 5, 6, 7, 8, 9} such that digits used are consecutive terms of a Geometric progression but not necessarily be in the order in the number formed as they are in GP and no digit is repeated?

1. 6

2. 18

3. 216

4. 3

Answer: 2

Possible geometric progressions are

[1, 2, 4]

[1, 3, 9]

[2, 4, 8]

From each set, numbers can be formed.

So, total numbers formed = Hence, the correct answer is 18.

Question:

How many 5-digit odd numbers can be formed using [1, 4, 9, 5] such that exactly 1 digit is repeated?

(TITA)

Answer: 240

Let digit ‘1’ is repeated; so, set of digits will be 1, 1, 9, 5, 4

Number of numbers formed =

Similarly for other digits; number of numbers formed = 60 for each case.

Total numbers formed = 4 x 60 = 240

CAT Ratio and Proportion Questions

Question:

A chemist mixes two liquids A and B in the ratio 3: 4. One litre of liquid A weighs 1 kg and one litre of liquid B weighs 900 gm. What is the difference between the weight of liquids in 3.5 litres of the mixture [in gms]?

(TITA)

Answer: 300

Since, the liquids are mixed in the ratio of 3: 4, quantity of liquid A in the mixture = 1.5 litres and that of liquid B is 2 litres.

Weight of 1.5 litres of liquid A = 1500 gms

Weight of 2 litres of liquid B = 1800 gms

Difference = 300 gms

CAT Averages Questions

Question:

In a company, there are three departments: Sales, Marketing, and Engineering. The average age of the Sales team is 30 years, the average age of the Marketing team is 35 years, and the average age of the Engineering team is 28 years. The total number of employees in the Sales department is 15, in the Marketing department is 20, and in the Engineering department is 25. What is the overall average age of the company's employees, considering all three departments?

1. 29.67

2. 30.05

3. 31.29

4. 30.83

Answer: 4

The Sales team has an average age of 30 years and 15 employees.

So, their total age is 30 × 15 = 450 years

The Marketing team has an average age of 35 years and 20 employees.

So, their total age is 35 × 20 = 700 years

The Engineering team has an average age of 28 years and 25 employees.

So their total age is 28 × 25 = 700 years

Total age of all employees = 450 years (Sales) + 700 years (Marketing) + 700 years (Engineering) = 1850 years

There are a total of 60 employees in the company (15 in Sales + 20 in Marketing + 25 in Engineering).

Overall average age = Total age of all employees / Total number of employees = 1850/60} = 30.83 years (rounded to two decimal places).

Hence, the correct answer is 30.83.

Question:

Onion is sold for 5 consecutive months at the rate of Rs. 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to:

1. 26

2. 18

3. 16

4. 20

Answer: 2

Let the family spend ₹100 for the first three months and spend ₹50 for the last two months.
Thus, the number of kilograms of onion bought in these 5 months, respectively, are 10, 5, 4, 2, 1.
The average expense for onion, in rupees per kg, for the family over these 5 months

Hence, the correct answer is 18.

For more practice and in-depth explanation of various CAT quantitative aptitude questions, click here: Download Now

CAT VARC Sample Questions

CAT DILR Sample Questions

Download Free Practice Questions with Detailed Solutions for CAT Quantitative Aptitude (QA) - MCQ PDFs