Mastering CAT Modern Math is easier when you understand the core concepts behind every question. The key topics in modern maths for CAT 2025 include permutations and combinations (PnC), probability, and set theory, which are used to solve problems related to counting, arrangements, distributions, and logical relationships in arithmetic and algebra. This article breaks down these essential concepts to help aspirants practice smarter, learn important CAT tricks for modern maths, and confidently tackle CAT quantitative aptitude problems based on PnC, probability, and sets.
The CAT 2025 result date has been announced. IIM Kozhikode will declare the results for 2.58 lakh candidates tomorrow, December 24, at 6 pm. Candidates can check their results by logging in with their valid CAT login credentials.
How These 3 Concepts Cover All Modern Math Questions
Strategy to Master Modern Math for CAT
Common Pitfalls & How to Avoid Them
CAT 2025 Preparation Resources by Careers360
Master CAT 2025 Modern Math: Permutations, Probability & Sets Made Simple
Why Modern Math is necessary for CAT
Modern maths is necessary for CAT 2025 although the topics under modern maths are not high-priority topics, as you can find 1 - 2 questions from it. These concepts form more complex problems in integration with the other topics like Arithmetic, Algebra, Number system, and Geometry. So, it becomes necessary to learn CAT modern maths.
For example:
To find the number of diagonals in regular polygon of n – sides, we use the concept of combination.
Number of diagonals in n-sided polygon = $^nC_2-n$
Weightage of Modern maths in CAT over the years:
It is important to understand the CAT Quantitative Aptitude weightage of each topic in past 4 to 5 years of the CAT exam to kick start our preparation for CAT.
S. No.
Year
Slot
Permutation and Combination
Probability
Sets
Total
1
2020
1
0
0
0
0
2
2020
2
0
0
0
0
3
2020
3
0
0
0
0
4
2021
1
1
0
0
1
5
2021
2
1
0
0
1
6
2021
3
1
0
0
1
7
2022
1
1
0
1
2
8
2022
2
1
0
0
1
9
2022
3
0
0
0
0
10
2023
1
0
0
0
0
11
2023
2
0
0
0
0
12
2023
3
0
0
0
0
13
2024
1
1
0
0
1
14
2024
2
0
0
0
0
15
2024
3
0
0
0
0
Why mastering modern math gives an edge
Questions from modern maths do not appear in bulk but still preparing it for CAT will give an edge. Advantages of preparing modern maths can be understood by following points:
The questions form modern maths topics like permutation and combination, are often formula based and direct.
Questions are conceptual but simple.
Modern topics like sets and probability are useful for LR DI questions. You can find use of Venn diagrams while solving the questions of Data Interpretation.
Preparing modern maths can give you an advantage because most of the aspirants focus on high priority topics like algebra and arithmetic. So, preparing modern maths along with these topics give you an edge.
CAT Modern maths questions boost your accuracy.
Great Lakes - PGDM & PGPM Admissions 2026
Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
Modern maths is not separate; it is just the extension of arithmetic and algebra with some new logics. It is important for us to know the interlinking of topics for CAT modern math preparation.
Set Theory & Venn Diagrams:
Set theory just does systematic counting. Representing the values in Venn diagram to find the desired value, can be represented by linear equations (Algebra).
It also uses the concept of percentage (Arithmetic).
Permutation & Combination:
Permutation and combination are fundamentally counting-based Arithmetic ie. Principle of addition and principle of multiplication.
Also, factorial simplification and binomial expansion are parts of Algebra which are used in PnC.
Probability:
What we do in probability is just the comparing with probable outcomes with total outcomes. It is equivalent to finding the ratios of two counts.
The most fundamental application of mathematics is counting. There are many natural methods used for counting. In this section, we are dealing with various known techniques those are much faster than the usual counting methods and useful for CAT questions.
The fundamental principle of counting is used to determine the total number of possible outcomes in a situation out of multiple independent events.
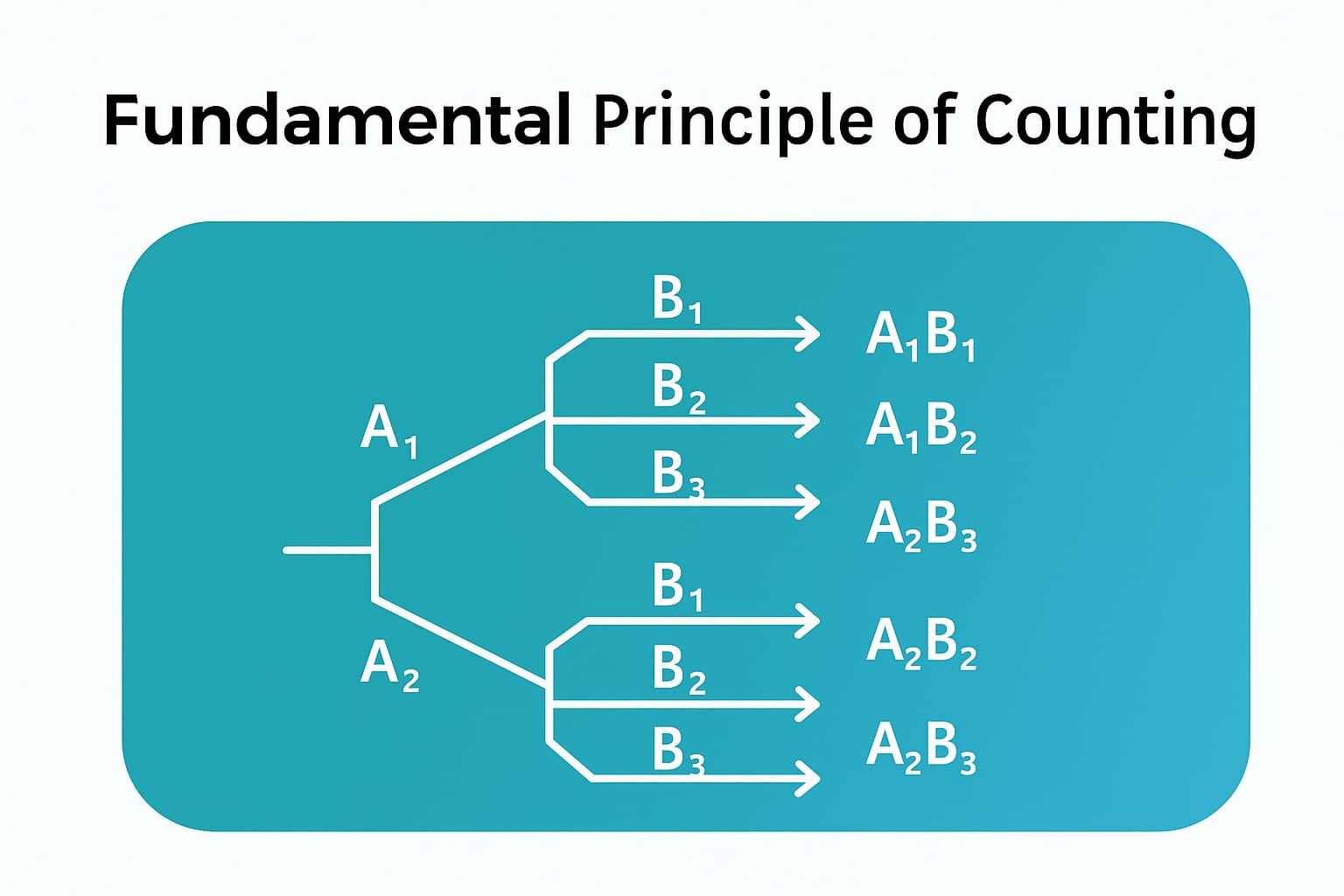
Let us understand this with a simple example:
Suppose you have two shirts ($A_1, A_2$) and three pairs of trousers ($B_1, B_2, B_3$), the question is in how many ways, you can dress yourself?
In this case, you are required to choose 1 shirt and 1 pair of trousers (Both are required). So, the possible combinations are $A_1B_1, A_1B_2, A_1B_3, A_2B_1, A_2B_2, A_2B_3$.
This is the fundamental principle of multiplication.
The formula: If you want to select 1 from n and 1 from m, then total number of combinations = $^nC_1 \times ^mC_1 = n \times m$
Suppose you have two pairs of shoes ($A_1, A_2$) and three pairs of slippers ($B_1, B_2, B_3$), the question is in how many ways, you can wear your footwear?
In this case, you are required to choose either 1 pair of shoes or 1 pair of slippers. So, the possible selections are $A_1, A_2, B_1, B_2, B_3$.
This is the fundamental principle of addition.
The formula: If you want to select 1 from n or 1 from m, then total number of selections = $^nC_1 + ^mC_1=n +m$
Permutations and Combinations:
How can we differentiate between Permutation and Combinations?
Combinations are used when we want to select r objects from n objects. (Selection only)
Total number of combinations = $^nC_r= \frac{n!}{(n-r)!r!}$
Permutations are used when we want to arrange r objects from n objects at r places. (Selection + Arrangement)
Total number of permutations = $^nP_r= \frac{n!}{(n-r)!}$
The Important Formulas and Concepts of Permutations and Combinations:
Concept
Formula
Number of permutations (or arrangements) of n different things taken all at a time
n!
Number of permutations of n things out of which P1 are alike and are of one type, P2 are alike and are of a second type and P3 are alike and are of a third type and the rest are all different
$\frac{n!}{(p_1)!(p_2)(p_3)}$
Number of selections of r things out of n identical things
1
Total number of selections of zero or more things out of k identical things
k + 1
Total number of selections of zero or more things out of n different things
$2^n$
Number of ways of distributing n identical things among r persons when each person may get any number of things
$^{n+r-1}C_{r-1}$
The total number of ways in which 0 to n things can be selected out of n things such that p are of one type, q are of another type and the balance r of different types is given by
(p + 1)(q + 1)(2r– 1)
Total number of ways of taking some or all out of p + q + r things such that p are of one type and q are of another type and r of a third type
(p + 1)(q + 1)(r + 1) – 1
Number of ways of arranging n people on a circular track (circular arrangement)
(n – 1)!
Permutations and Combinations Practice Questions for CAT:
Question 1: How many numbers between 10 and 10,000 can be formed by using the digits 1, 2, 3, 4, 5 if
(i) No digit is repeated in any number.
(ii) Digits can be repeated.
Solution: (i) Number of two-digit numbers = 5 × 4 = 20
Number of three-digit numbers = 5 × 4 × 3 = 60
Number of four-digit numbers = 5 × 4 × 3 × 2 = 120
Total = 200
(ii) Number of two-digit numbers = 5 × 5 = 25
Number of three-digit numbers = 5 × 5 × 5 = 125
Number of four-digit numbers = 5 × 5 × 5 × 5 = 625
Total = 775
Question 2: How many three-digit numbers can be formed using the digits 1, 2, 3, 4, 5, without repetition of digits?
How many of these are even?
Solution: Three places are to be filled with 5 different objects.
Number of ways = $^5P_3 = 5 × 4 × 3 = 60$
For the 2nd part, unit digit can be filled in two ways & the remaining two digits can be filled
in $^4P_2=12$ ways.
Number of even numbers = 2 × 12 = 24.
Question 3: There are fifteen players for a cricket match.
(i) In how many ways the 11 players can be selected?
(ii) In how many ways the 11 players can be selected including a particular player?
(iii) In how many ways the 11 players can be selected excluding two particular players?
Solution: (i) 11 players are to be selected from 15
Number of ways = $^15C_11 = 1365$.
(ii) Since one player is already included, we have to select 10 from the remaining 14
Number of ways = $^14C_10 = 1001$.
(iii) Since two players are to be excluded, we have to select 11 from the remaining 13.
Number of ways = $^13C_11 = 78$.
Concept 2: Selection & Grouping in Probability
Probability in CAT constitutes the questions based on basic formula, binomial, and conditional probability. These questions use the concept of election and grouping.
Probability is the logic of uncertainty and randomness. Uncertainty in an event and randomness of an event is a part our daily life. So, it becomes more interesting to understand probability.
How grouping, selection, and distribution link to probability?
Grouping, selection, and distribution are integrated part of probability as to describe the likely events or outcomes within a group, we use concept of selection and grouping (Combinations).
Total outcomes is a defined set, which we calculate using the concept of combinations
[Selecting r from n]. Probability determines the chance of a specific selection.
Important Formulas and Concepts on Probability:
1. Random Experiment
If all the possible outcomes of an experiment are known but the exact output cannot be predicted in advance, that experiment is called a random experiment.
Examples
(i) Tossing of a fair coin
When we toss a coin, the outcome will be either Head (H) or Tail (T)
(ii) Throwing an unbiased die
Die is a small cube used in games. It has six faces and each of the six faces shows a different number of dots from 1 to 6. Plural of die is dice.
When a die is thrown or rolled, the outcome is the number that appears on its upper face and it is a random integer from one to six, each value being equally likely.
(iii) Drawing a card from a pack of shuffled cards
A pack or deck of playing cards has 52 cards which are divided into four categories as given below
a. Spades (♠) [Black: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]
b. Clubs (♣) [Black: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]
c. Hearts (♥) [Red: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]
d. Diamonds (♦) [Red: Total = 13, 9 number cards numbered from 2 to 10, 4 honour card: an Ace, a King, a Queen and a jack]
Kings, Queens and Jacks are called face cards
CAT 2025 Percentile Predictor
Use the CAT Percentile Predictor to estimate your score, gauge your performance, and know your chances of getting shortlisted by IIMs.
Sample Space is the set of all possible outcomes of an experiment. It is denoted by S.
Examples
(i) When a coin is tossed, S = {H, T} where H = Head and T = Tail
(ii) When a dice is thrown, S = {1, 2 , 3, 4, 5, 6}
(iii) When two coins are tossed, S = {HH, HT, TH, TT} where H = Head and T = Tail
3. Event
Any subset of a Sample Space is an event. Events are generally denoted by capital letters A, B, C, D etc.
Examples
(i) When a coin is tossed, outcome of getting head or tail is an event
(ii) When a die is rolled, outcome of getting 1 or 2 or 3 or 4 or 5 or 6 is an event
4. Equally Likely Events
Events are said to be equally likely if there is no preference for a particular event over the other.
Examples
(i) When a coin is tossed, Head (H) or Tail is equally likely to occur.
(ii) When a dice is thrown, all the six faces (1, 2, 3, 4, 5, 6) are equally likely to occur.
5. Mutually Exclusive Events
Two or more than two events are said to be mutually exclusive if the occurrence of one of the events excludes the occurrence of the other.
This can be better illustrated with the following examples
(i) When a coin is tossed, we get either Head or Tail. Head and Tail cannot come simultaneously. Hence occurrence of Head and Tail are mutually exclusive events.
(ii) When a die is rolled, we get 1 or 2 or 3 or 4 or 5 or 6. All these faces cannot come simultaneously. Hence occurrences of
6. Independent Events
Events can be said to be independent if the occurrence or non-occurrence of one event does
not influence the occurrence or non-occurrence of the other.
Example: When a coin is tossed twice, the event of getting Tail(T) in the first toss and the event of getting Tail(T) in the second toss are independent events. This is because the occurrence of getting Tail(T) in any toss does not influence the occurrence of getting Tail(T) in the other toss.
7. Exhaustive Events
Exhaustive Event is the total number of all possible outcomes of an experiment.
Examples:
(i) When a coin is tossed, we get either Head or Tail. Hence there are 2 exhaustive events.
(ii) When two coins are tossed, the possible outcomes are (H, H), (H, T), (T, H), (T, T). Hence there are 4 (= 22) exhaustive events.
(iii) When a dice is thrown, we get 1 or 2 or 3 or 4 or 5 or 6. Hence there are 6 exhaustive events.
8. Algebra of Events
Let A and B are two events with sample space S. Then
(i) A ∪ B is the event that either A or B or Both occur. (i.e., at least one of A or B occurs)
(ii) A ∩ B is the event that both A and B occur
(iii) is the event that A does not occur
(iv) is the event that none of A and B occurs
Example: Consider a die is thrown, A be the event of getting 2 or 4 or 6 and B be the event of getting 4 or 5 or 6. Then
A = {2, 4, 6} and B = {4, 5, 6}
A ∪ B = {2, 4, 5, 6}
A ∩ B = {4, 6}
Concept
Formula
Probability of sample space
P(S) = 1
Let A and B be two events associated with a random experiment
P(A U B) = P(A) + P(B) – P(A ∩ B)
If A and B are mutually exclusive events, then P(A U B) = P(A) + P(B) because for mutually exclusive events, P(A ∩ B) = 0
If A and B are two independent events, then
P(A ∩ B) = P(A).P(B)
Let E be an event associated with a random experiment. Let x outcomes are favourable to E and y outcomes are not favourable to E, then
Odds in favour of E are x/y and
Odds against E are y/x
A binomial experiment is a probability experiment which satisfies the following requirements.
1. Each trial can have only two outcomes. These outcomes can be considered as either success or failure.
2. There must be a fixed number of trials.
3. The outcomes of each trial must be independent of each other.
4. The probability of a success must remain the same for each trial.
In a binomial experiment, the probability of achieving exactly r successes in n trials can be given by
P (r successes in n trials) = $^nC_r \times p^r \times q^{n-r}$
In CAT, direct questions are not generally asked from Sets but this topic has importance in the questions of percentage, data interpretation, function, and other related topics.
In this section, we are going to discuss some important concepts related to set.
A set is a well-defined collection of elements. By well-defined elements it means that given a set and an element, it must be possible to decide whether or not the element belongs to the set.
How the sets are represented?
Sets are represented in two ways:
1. Roaster Form:
A set is described by listing elements, separated by commas, within brackets.
For example: Set of all prime numbers less than 20
A = {2, 3, 5, 7, 11, 13, 17, 19}
2. Set Builder Form:
A set can also be described by a characterizing property of the elements in the set.
For example: Set of all prime numbers less than 20
A = {x: x is a prime number less than 20}
Important concepts regarding sets:
Subset:
If every element of A is contained in B, then A is called the subset of B.
If A is subset of B, we write A ⊂ B, which is read as "A is a subset of B".
Null set:
Null set contains no elements, represented by ø or { }.
Power Set:
The set of subsets of a set is the power set of the set. If A is a set, then its Power set is denoted as P(A).
If A = {a, b, c}, then P(A) = {φ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
Universal Set:
In any discussion in theory, there happens to be a set U that contains all sets under consideration. Such a set is called the universal set.
For example, in plane geometry the set of all points in the plane is the universal set.
Operations on Sets:
Union of Sets
The union of two sets A and B contains all the elements present in set A or in set B.
So, A U B = {x | x ∈ A or x ∈ B}
For example:
A = {5, 7, 8, 9, 11} and B = {7, 8, 12, 14} then
A U B = {5, 7, 8, 9, 11, 12, 14}
Intersection of Sets
The intersection of two sets A and B contains only common elements present in set A or in set B.
So, A ∩ B = {x | x ∈ A and x ∈ B}
For example:
A = {5, 7, 8, 9, 11} and B = {7, 8, 12, 14} then
A ∩ B = {7, 8}
Difference of sets
A – B is the difference of set A from set B and is defined as the set of elements
present in set A but not in set B.
So, A – B = {x | x ∈ A and x ∉ B}
For example:
A = {5, 7, 8, 9, 11} and B = {7, 8, 12, 14} then
A - B = {5, 9, 11}
Complement of a set
The complement of set A in U the set of those elements which are present in Universal set but not present in
set A. Compliment of A is denoted by A'.
So, A‘= {x | x ∈ U and x ∉ A}
For example:
A = {5, 7, 8, 9, 11} and U = {5, 7, 8, 9, 11, 12, 14} then
A’ = {12, 14}
Concept of Venn diagram
Sets can be represented with the help of pictorial diagram using Venn diagram. Circles are used to represent the sets; common part of two intersecting circles represents the common elements of two sets. We generally use a rectangle to represent the universal set.
Example:
1.
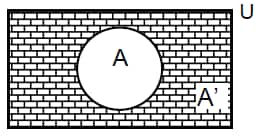
Shaded portion = A’ = compliment of A
2.
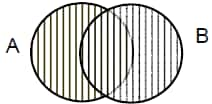
Shaded portion = A U B
3.
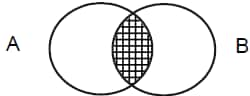
Shaded portion = A ∩ B
4.
AB
Shaded part = A – B
Sets and Venn diagram Practice Questions for CAT:
Question 1: In a certain city only two newspapers A & B are published. It is known that 25% of the city population reads A & 20% read B while 8% read both A & B. It is also known that 30% of those who read A but not B, look into advertisements and 40% of those who read B but not A, look into advertisements while 50% of those who read both A & B look into advertisements. What % of the population reads an advertisement?
Solution:
Let A & B denote sets of people who read paper A & paper B respectively and in all there are 100 people, then n(A) = 25, n(B) = 20, n (A ∩ B) = 8.
Hence the people who read paper A only i.e. n(A – B) = n (A) – n(A ∩ B) = 25 – 8 = 17.
And the people who read paper B only i.e. n(B – A) = n (B) – n (A ∩ B) = 20 – 8 = 12.
Now percentage of people reading an advertisement
= [(30% of 17) + (40% of + 12) + (50% of 8)]% = 13.9 %.
Question 2: In a prestigious business institute in north India, there are three specializations in business course and a student is can choose as many specializations as he wants. These specializations are Finance, Marketing and HRD. If 120 students specialize in Finance, 110 in Marketing and 125 are in HRD. 90 students have finance and Marketing both as their specialization, 85 have marketing and HRD while 80 have both finance and HRD. What can be the minimum and maximum number of students who can specialization in all the three fields?
Solution: Based on information given in the question, we can draw following Venn diagram
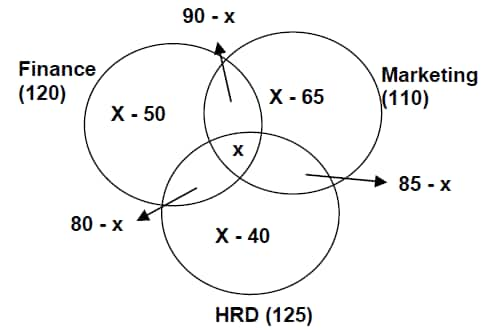
To find the minimum value of x, we have x – 65 ≥ 0 ⇒ x ≥ 65
And for maximum value of x, we have 80 – x ≥ 0 ⇒ x ≤ 80
Hence 65 ≤ x ≤ 80. So, we have the range of the values that can be the required solution.
How These 3 Concepts Cover All Modern Math Questions
CAT Preparation Strategy involves continuous practice and revision of key concepts. Here’s a step-by-step strategy to master Modern Math for CAT covering topics like Permutations & Combinations, Probability, Set Theory, and Functions. You need to create a CAT preparation time table to prepare modern maths for CAT and then follow the given steps.
Step 1: Build strong foundation, conceptual knowledge of each topic.
Step 2: Focus on logic before formulae.
Step 3: Understand the interlinking of modern maths topics with the other section of Quantitative Aptitude like arithmetic, algebra etc.
Also, understand how the questions will form using the integration of these questions and practice accordingly.
Step 4: Prioritize high yield topics according to last 5 years trend.
Step 5: Solve NCERT questions to build concepts.
Step 6: Practice with previous year CAT questions.
Step 7: Practice mock tests and analyse them to manage your time, accuracy, and speed.
Common Pitfalls & How to Avoid Them
In this section we are dealing with the common mistakes, a student does often make while preparing for CAT and attempting questions during exam. Also, you should know how to tackle them.
Common Mistakes
How to tackle
Memorizing formulas without logic
Do not learn direct formulas without knowing the concept because small variation in question may lead you to the wrong answer if you don’t know the logic behind it. Learn the logic first and then memorise the formula by using that in CAT type questions.
Confusion between arrangements and selections
Sometimes students get confused which concept is to be used: Combination or Permutation
If grouping or selection is required, use combination.
If after selection, arrangement also required, then permutation is to be used.
Mistakes in writing the solution sets
Here you should understand which bracket is to be used to represent the solution set.
A ϵ {1, 2, 3}, it means A can have three values 1, 2, and 3 only.
A = [1, 9], it means A can be any real number between 1 to 9 including 1 and 9.
A = (1, 9), it means A can be any real number between 1 to 9 excluding 1 and 9.
A = (1, 9], it means A can be any real number between 1 to 9 including 9 but excluding 1.
A = [1, 9), it means A can be any real number between 1 to 9 including 1 but excluding 9.
Not practicing enough CAT-level questions.
Since the modern maths is not high weightage section, student often avoiding enough practice on CAT level question from this topic. You should solve enough CAT level questions which helps you to understand the pattern of integrated questions with other topics.
Best books and online resources for Modern Maths CAT prep
1. NCERT Mathematics Class 11 and 12
2. How to prepare quantitative Aptitude for CAT by Arun Sharma.
3. Quantitative Aptitude for CAT by Nishit K Sinha
CAT 2025 Preparation Resources by Careers360
The candidates can download the various CAT preparation resources designed by Careers360 using the links given below.
eBook Title
Download Links
CAT 2025 Arithmetic Important Concepts and Practice Questions
CAT does not restrict eligibility based on stream. Candidates from commerce, arts, science, engineering or any other background can appear for CAT and apply to MBA programmes offered by IIMs and other top B-schools.
The basic eligibility criteria for CAT are:
You must hold a bachelor’s degree in any discipline from a recognised university with at least 50 percent marks (45 percent for SC, ST and PwD categories). Final-year graduation students are also eligible to apply.
Being a commerce graduate can actually be an advantage in areas such as accounting, finance, economics and business studies, especially during MBA coursework in finance, marketing and operations.
After qualifying CAT, admission depends on multiple factors including CAT percentile, academic background, work experience (if any), performance in GD, WAT and personal interview rounds. Many IIMs and B-schools follow a diverse academic background policy, which means non-engineering candidates, including commerce graduates, often receive additional weightage.
Apart from IIMs, several reputed institutes such as FMS Delhi, SPJIMR Mumbai, MDI Gurgaon, IMT Ghaziabad, and many state and private universities also accept CAT scores for MBA admissions.
So, as a commerce graduate, you are fully eligible to appear for CAT and pursue an MBA, provided you meet the minimum academic requirements and perform well in the selection process.
If you want, I can also help you with realistic CAT percentile targets based on your academic profile or suggest suitable MBA colleges.
With a CAT 2025 raw score of 84 and strong sectionals, your expected percentile may fail in the high 98 range , depending on scaling. Your excellent academics and 2 years of work experience strengthen your profile .IIM Lucknow calls are possible but competitive for EWS engineers , while FMS Delhi looks mainly at CAT score and VARC , so you have a reasonable chance there . Final calls depend on cutoffs and composite score.
For MANAGE Hyderabad MBA , the OBC cutoff in CAT 2024 was generally around 85-90 percentile for shortlist consideration , tough exact figures vary by section and profile . For CAT 2025, if fewer candidates appeared , the cutoff might slightly adjust , but percentile based cutoffs dont change drastically year to year. A minor decrease is possible , but you should still aim for 90+ percentile to be competitive. Factors like VARC, QA-LRDI and overall profile influence the final shortlist.
For a raw score of 56 in CAT 2025 Slot 3, your expected overall percentile is likely to be in the range of the 90th-95th percentile. The exact percentile can vary slightly on the final normalization process and the process and performance of all test-takers. In this
article
you'll find more about the CAT result.
Hello,
With a projected CAT percentile of 87% but not clearing sectional cutoffs, your chances at top IIMs are limited because they require both overall percentile and sectional minimums. However, you still have a good shot at other reputed management institutes and non-IIM B-schools. Consider colleges like NMIMS, SPJIMR, IMT, TAPMI, Great Lakes, and other well-ranked private or state-level B-schools that accept CAT scores and weigh your profile holistically. Your academic record, BSc in Animation with 80%, and 5 years of work experience at Ubisoft India are strong points and may help in institutes that value work experience in their selection process. Also, explore institutes that accept XAT, MAT, or CMAT, where your profile can be competitive.
Hope this helps you.
A career as Marketing Director is also known as a marketing expert who is responsible for the overall marketing aspect of the company. He or she oversees plans and develops the company's budget. The marketing Director collaborates with the business team to plan and develop the marketing and branding strategies for the company's products or services.
A Business Development Executive identifies and pursues new business opportunities to drive company growth. They generate leads, build client relationships, develop sales strategies, and analyse market trends. Collaborating with internal teams, they aim to meet sales targets. With experience, they can advance to managerial roles, playing a key role in expanding the company’s market presence and revenue.
Content Marketing Specialists are also known as Content Specialists. They are responsible for crafting content, editing and developing it to meet the requirements of digital marketing campaigns. To ensure that the material created is consistent with the overall aims of a digital marketing campaign, content marketing specialists work closely with SEO and digital marketing professionals.
A Sales Manager leads a sales team to meet targets, formulates strategies, analyses performance, and monitors market trends. They typically hold a degree in management or related fields, with an MBA offering added value. The role often demands over 40 hours a week. Strong leadership, planning, and analytical skills are essential for success in this career.
A marketing manager is a person who oversees a company or product marketing. He or she can be in charge of multiple programmes or goods or can be in charge of one product. He or she is enthusiastic, organised, and very diligent in meeting financial constraints. He or she works with other team members to produce advertising campaigns and decides if a new product or service is marketable.
A Marketing manager plans and executes marketing initiatives to create demand for goods and services and increase consumer awareness of them. A marketing manager prevents unauthorised statements and informs the public that the business is doing everything to investigate and fix the line of products. Students can pursue an MBA in Marketing Management courses to become marketing managers.
An SEO Analyst is a web professional who is proficient in the implementation of SEO strategies to target more keywords to improve the reach of the content on search engines. He or she provides support to acquire the goals and success of the client’s campaigns.
Digital marketing is growing, diverse, and is covering a wide variety of career paths. Each job function aids in the development of effective digital marketing strategies and techniques. The aims and objectives of the individuals who opt for a career as a digital marketing executive are similar to those of a marketing professional: to build brand awareness, promote company services or products, and increase conversions. Individuals who opt for a career as Digital Marketing Executives, unlike traditional marketing companies, communicate effectively through suitable technology platforms.
Individuals who opt for a career as a business analyst look at how a company operates. He or she conducts research and analyses data to improve his or her knowledge about the company. This is required so that an individual can suggest the company strategies for improving their operations and processes.
In a business analyst job role a lot of analysis is done, things are learned from past mistakes and the successful strategies are enhanced further. A business analyst goes through real-world data in order to provide the most feasible solutions to an organisation. Students can pursue Business Analytics to become Business Analysts.
2 Jobs Available
Never miss CAT update
Get timely CAT updates directly to your inbox. Stay informed!
B
