Top 5 Important Question Types That Always Appear in CAT Quantitative Aptitude

Question Type 1: Based on Time, Speed and Distance

Topic: Time, speed, and distance

Key concept used: Relative Speed and Average Speed

Questions are based on two trains/cars moving towards each other, going away, and we need to find the average speed, time of meeting, or distance between them at any point of time etc. So, it is suggested that you should practice the questions based on this concept.

Key Concept and Formula:

Concept of Relative Speed:

Two Objects are moving in same direction:

When two objects are moving in the same direction, their relative speed with respect to each other is the difference of their speeds.

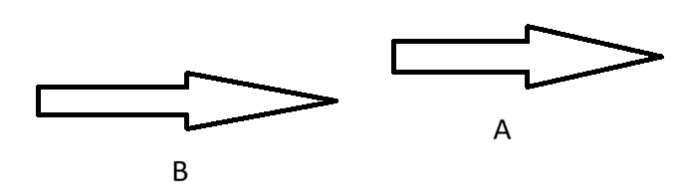
Speed of B with respect to A = SB – SA (SB > SA)

Where:

SA is the speed of A.

SB is the speed of B.

Two Objects are moving in opposite direction:

When two objects are moving in the opposite direction, their relative speed with respect to each other is the sum of their speeds.

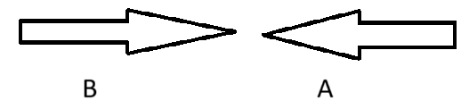
Speed of B with respect to A = SB + SA

Concept of Average Speed:

Average speed is not simply the arithmetic mean of various speeds. Instead, it takes into account the total distance covered and the total time taken. The formula for average speed is:

Average Speed = $\frac {\text{Total Distance Covered}}{\text{Total Time Taken}}$

Short tricks:

1. If two equal distances are covered at speeds S1 and S2, then

Avg speed = $\frac{2S_1 S_2}{S_1+S_2}$

(If two distances covered at different speeds are equal, the average speed is the harmonic mean of the two speeds)

2. If two distances are covered at speeds S1 and S2 for equal time, then

Avg speed = $\frac{S_1 + S_2}{2}$

Previous Years' Questions Based on Time, Speed and Distance

Q.1) Two places A and B are 45 kms apart and connected by a straight road. Anil goes from A to B while Sunil goes from B to A. Starting at the same time, they cross each other in exactly 1 hour 30 minutes. If Anil reaches B exactly 1 hour 15 minutes after Sunil reaches A, the speed of Anil, in km per hour, is

A) 12

B) 16

C) 18

D) 20

Solution:-

Let the speeds of Anil and Sunil be $a$ and $s$ respectively.
They meet after 1.5 hours, and the distance between A and B is 45 km.
It implies that both together have travelled 45 Km in 1.5 hrs.
So,
$(a + s) \times 1.5 = 45$
$⇒ a + s = 30 \quad ------\text{(i)}$

Let the time taken by Sunil after the meeting be $t$ hours.
Then the time taken by Anil after the meeting is $t + \frac{5}{4}$ hours.
For the given situation, the Time taken ($T$) to meet by A and B is equal to the product of the time taken by A ($T_1$) and B ($T_2$) to reach their respective destination after meeting is given by
$T=\sqrt {T_1 \times T_2}$
So,
$
\frac{3}{2} = \sqrt{t \cdot \left(t + \frac{5}{4} \right)}
$
$⇒
\left( \frac{3}{2} \right)^2 = t^2 + \frac{5t}{4}
$
$⇒
\frac{9}{4} = t^2 + \frac{5t}{4}
$
$⇒
4t^2 + 5t - 9 = 0
$
$⇒4t^2+9t-4t-9=0$
$⇒(4t+9)(t-1)=0$
So, $t=1,-\frac{9}{4}$

We get $t = 1$ hour (only positive value is valid).

So, the time taken by Anil after the meeting: $
1 + \frac{5}{4} = \frac{9}{4} \text{ hours}
$
Total time taken by Anil: $
\frac{3}{2} + \frac{9}{4} = \frac{15}{4} \text{ hours}
$
Speed of Anil: $
\frac{45}{\frac{15}{4}} = \frac{45 \times 4}{15} = 12 \text{ km/h}
$

Hence, the correct answer is option 1.

Q.2) Brishti went on an 8-hour trip in a car. Before the trip, the car had travelled a total of x km till then, where x is a whole number and is palindromic, i.e., x remains unchanged when its digits are reversed. At the end of the trip, the car had travelled a total of 26862 km till then, this number again being palindromic. If Brishti never drove at more than 110 km/hr, then the greatest possible average speed at which she drove during the trip, in km/hr, was:

A) 90

B) 100

C) 80

D) 90

Solution:-

Let the speed of Brishti be $y$ km/hr.
So, according to the question,
$26862-8 y=x$
From options, we can find that the only possible value for $y$ is 100 for $x$ to be palindromic.
Hence, the correct answer is option (2).

Q.3) Trains A and B start traveling at the same time towards each other with constant speeds from stations X and Y, respectively.
Train A reaches station Y in 10 minutes while train B takes 9 minutes to reach station X after meeting train A. Then the total time taken, in minutes, by train B to travel from station Y to station X is:

A) 6

B) 15

C) 10

D) 12

Solution:-

M – First meeting pointLet the speeds of trains A and B be ‘a’ and ‘b’, respectively.
$
\frac{x}{a}=\frac{D-x}{b}
$
It is given,
$
\begin{aligned}
& \frac{D}{a}=10 \text { and } \frac{x}{b}=9\\\
& \frac{x}{\frac{D}{10}}=\frac{D-x}{\frac{x}{9}}\ [\text{After putting the values}] \\
& ⇒\frac{10 x}{D}=\frac{9 D-9 x}{x} \\
&⇒ 10 x^2=9 D^2-9 D x \\
& ⇒10 \mathrm{x}^2+9 \mathrm{Dx}-9 \mathrm{D}^2=0
\end{aligned}
$
Solving, we get, $ x=\frac{3 D}{5}$
Solving, we get,
$
\frac{x}{b}=9
$
$\begin{aligned} &⇒ \frac{3 D}{b \times 5}=9 \\ & ⇒\frac{D}{b}=15\end{aligned}$

The total time taken by train B to travel from station Y to station X is 15 minutes.
Hence, the correct answer is option (2).

Question Type 2: Based on Ration and Proportion

Topic: Ratio and Proportion

Key concept used: Ratio, Percentage change

Questions are based on the ratio of salaries, percentage change in salaries, ratio of male and female, ratio of employees etc. So, you should take on to practice the questions based on this concept.

Key Concept and Formula:

The Calculation of a ratio: Percentage and decimal values

A ratio is a comparison between two quantities, showing the relative size of one quantity to another. It is often expressed in the form 'a:b', where "a" and "b" are the two quantities.

Converting Ratio to Percentage:

Given a ratio 'a:b', the percentage representation of "a" in terms of the whole (a+b) is given by:

Percentage of a = $\frac {a}{a+b} × 100 \%$

Converting Ratio to Decimal:

Given a ratio 'a:b', the decimal representation of "a" in terms of the whole (a+b) is $\frac {a}{a+b}$.

Percentage Change:

To find a certain percentage of a number, multiply the number by that percentage.

% change = $\frac {\text{(New Value-Old Value)}}{\text{Old Value}} × 100 \%$

Previous Years' Questions Based on Ration and Proportion

Q.1) A fruit seller has a total of 187 fruits consisting of apples, mangoes and oranges. The number of apples and mangoes are in the ratio $5: 2$. After she sells 75 apples, 26 mangoes and half of the oranges, the ratio of number of unsold apples to number of unsold oranges becomes $3: 2$. The total number of unsold fruits is

A) 66

B) -

C) -

D) -

Solution:-

Let the number of apples and mangoes be $5x$ and $2x$ respectively.

Then, number of oranges = $187 - 5x - 2x = 187 - 7x$

Apples sold = $75$, so unsold apples = $5x - 75$
Mangoes sold = $26$, so unsold mangoes = $2x - 26$
Oranges sold = half, so unsold oranges = $\frac{1}{2}(187 - 7x)$

Given: $\frac{5x - 75}{\frac{1}{2}(187 - 7x)} = \frac{3}{2}$

Cross-multiplying: $2(5x - 75) = 3 \cdot \frac{1}{2}(187 - 7x)$
$⇒10x - 150 = \frac{3}{2}(187 - 7x)$
$⇒10x - 150 = \frac{561 - 21x}{2}$
$⇒20x - 300 = 561 - 21x$
$⇒41x = 861 \Rightarrow x = 21$

So, apples = $5x = 105$, mangoes = $2x = 42$, oranges = $187 - 147 = 40$

Unsold fruits:
Apples = $105 - 75 = 30$
Mangoes = $42 - 26 = 16$
Oranges = $40/2 = 20$

Total unsold = $30 + 16 + 20 = 66$

Hence, the correct answer is $66$.

Q.2) The salaries of three friends Sita, Gita, and Mita are initially in the ratio 5:6:7, respectively. In the first year, they get salary hikes of 20%, 25%, and 20%, respectively. In the second year, Sita and Mita get salary hikes of 40% and 25%, respectively, and the salary of Gita becomes equal to the mean salary of the three friends. The salary hike of Gita in the second year is:

A) 26%

B) 28%

C) 25%

D) 30%

Solution:-

Let the initial salaries of Sita, Gita and Mita be 500, 600 and 700 respectively.
After getting 20%, 25% and 20% salary hikes respectively, their salaries become 600, 750 and 840 respectively.
In the second year, Sita and Mita get 40% and 25% hikes respectively.
So, after two years the salaries of Sita and Mita are 840 and 1050 respectively.
We also know that Gita’s salary is the average of the salaries of the three which is equal to the average of the other two i.e. $\frac{840+1050}{2} = 945$
So, the hike in the salary of Gita during the second year = $\frac{945-750}{750} \times 100 = 26$%
Hence, the correct answer is option (1).

Q.3) Pinky is standing in a queue at a ticket counter. Suppose the ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3:5. If the total number of persons in the queue is less than 300, then the maximum possible number of persons standing ahead of Pinky is:

A) 111

B) 222

C) 333

D) 233

Solution:-

Let’s assume that there are $3a$ number of people ahead of Pinky, then the number of people behind her will be $5a$.
The total number of people in the queue is $8a + 1$.
Since the total number of people in the queue is less than 300,
$8a + 1 < 300$
⇒ $a ≤ 37$
To find the maximum number of people ahead of Pinky, we take the maximum possible value of $a$, which is 37.
Therefore, the maximum number of people ahead of Pinky is = (3 × 37) = 111
Hence, the correct answer is option (1).

Question Type 3: Based on Mixture and Alligation

Topic: Mixture and Alligation

Key concept used: Concept of Replacement

Mixture and allegation is a key concept for CAT QA. You will find question on replacement almost every in CAT QA. Questions are based on the replacement or addition of one ingredient.

Key Concept and Formula:

Suppose a vessel contains x litres of liquid A and if b litres be withdrawn and replaced by liquid B, if this process is repeated n times, then,

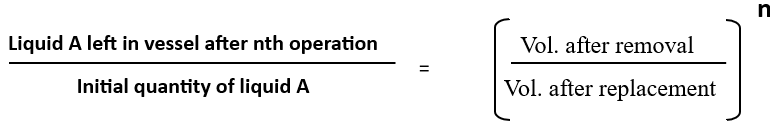
Note: 1) Here initial volume and final volume of the vessel will be same

2) In the final solution we will get both liquid A and B both of total volume x litres, so we have:

Liquid A left + Liquid B left = x, Liquid A left can easily be calculated by above formula then Liquid B left = x – Liquid A left.

Previous Years’ Questions Based on Mixture and Alligation

Q.1) A glass is filled with milk. Two-thirds of its content is poured out and replaced with water. If this process of pouring out two-thirds the content and replacing with water is repeated three more times, then the final ratio of milk to water in the glass, is

A) 1:80

B) 1:81

C) 1:26

D) 1:24

Solution:-

Let the initial quantity of milk = 1 unit
At each step, $\frac{2}{3}$ of the mixture is removed and replaced with water.

So, after each step, milk left = $\frac{1}{3}$ of previous milk quantity.

After 1st step: Milk left = $\frac{1}{3}$
After 2nd step: Milk left = $\frac{1}{3} \times \frac{1}{3} = \frac{1}{9}$
After 3rd step: Milk left = $\frac{1}{9} \times \frac{1}{3} = \frac{1}{27}$
After 4th step: Milk left = $\frac{1}{27} \times \frac{1}{3} = \frac{1}{81}$

After 4 such steps:

Milk left = $1 \times \left(\frac{1}{3}\right)^4 = \frac{1}{81}$
Water = $1 - \frac{1}{81} = \frac{80}{81}$

Final ratio of milk to water = $\frac{1}{81} : \frac{80}{81} = 1 : 80$

Hence, the correct answer is option 1.

Q.2) A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with the same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in mixture Q is 16:9, then the ratio of cocoa in mixture P to that in mixture Q is:

A) 4:9

B) 1:3

C) 5:9

D) 5:8

Solution:-

$\text{Proportion of Coffee after two replacements}$
$=\text{Initial Proportion of Coffee} × (\frac{\text{Volume before addition after each replacement}}{\text{Volume after addition}})^{(\text{Number of replacements)}}$
Let the total volume be 25 units (16 units of coffee and 9 units of cocoa).
Initially, The solution contains 25 units of coffee and 0 units of cocoa powder.
Also, Let $x$ units of solution be removed every time.
Using above formula
$\frac {16}{25} = 1 (\frac{25 - x}{25})^2$
On solving, we get $x = 5$
So, the required ratio $= 5:9$
Hence, the correct answer is option (3).

Q.3) A mixture contains lemon juice and sugar syrup in equal proportion. If a new mixture is created by adding this mixture and sugar syrup in the ratio 1 : 3, then the ratio of lemon juice and sugar syrup in the new mixture is:

A) 1 : 4

B) 1 : 5

C) 1 : 6

D) 1 : 7

Solution:-

Lemon juice: sugar syrup in the mixture is 1:1, i.e. 50% Lemon juice and 50% sugar syrup.
In sugar syrup, 100% is sugar syrup.
These two are mixed in the ratio 1 : 3.
Lemon juice = $\frac{1(50 \%)}{1+3}$
Sugar syrup = $\frac{1(50 \%)+3(100 \%)}{1+3}=\frac{350}{4}$
Required ratio = 50 : 350 = 1 : 7
Hence, the correct answer is 1 : 7.

Question Type 4: Based on Average

Topic: Average

Key concept used: Average and Weighted average

Questions based on the concept of average in CAT includes the concept of ages, percentage, salaries, population, number of persons added or leaving a group, number properties, AM & GM etc. Every year you will find 1 or 2 question on average directly or indirectly.

Key Concept and Formula:

The average of a set of numbers is the sum of those numbers divided by the count of the numbers.

Mathematically:

Average = $\frac {\text{Sum of all numbers}}{\text{Count of all numbers}}$

The weighted average (or weighted mean) is an average in which each quantity in the dataset is assigned a weight. These weights determine the relative importance of each quantity on the average.

Mathematically:

Average = $\frac{n_1x_1+n_2x_2+...}{n_1+n_2+....}$

Where, x1, x2, x3, … are the averages of n1, n2, n3, … observations respectively.

Previous Years’ Questions Based on Average

Q.1) There are four numbers such that average of first two numbers is 1 more than the first number, average of first three numbers is 2 more than average of first two numbers, and average of first four numbers is 3 more than average of first three numbers. Then, the difference between the largest and the smallest numbers, is __________.

Solution:-

Let the four numbers be $a, b, c, d$.

Given:
Average of first two numbers is 1 more than the first number:

$\frac{a + b}{2} = a + 1 \Rightarrow a + b = 2a + 2 \Rightarrow b = a + 2$

Average of first three numbers is 2 more than average of first two numbers:

$\frac{a + b + c}{3} = \frac{a + b}{2} + 2$

Substitute $b = a + 2$:

We get $\frac{a + (a + 2) + c}{3} = \frac{a + (a + 2)}{2} + 2$

$⇒\frac{2a + 2 + c}{3} = \frac{2a + 2}{2} + 2$

$⇒\frac{2a + 2 + c}{3} = a + 1 + 2 = a + 3$

$⇒2a + 2 + c = 3a + 9 \Rightarrow c = a + 7$

Average of all four numbers is 3 more than average of first three:

$\frac{a + b + c + d}{4} = \frac{a + b + c}{3} + 3$

Substitute $b = a + 2$, $c = a + 7$:

$\frac{a + (a + 2) + (a + 7) + d}{4} = \frac{a + (a + 2) + (a + 7)}{3} + 3$

$⇒\frac{3a + 9 + d}{4} = \frac{3a + 9}{3} + 3$

$⇒\frac{3a + 9 + d}{4} = a + 3 + 3 = a + 6$

$⇒3a + 9 + d = 4a + 24 \Rightarrow d = a + 15$

Now the four numbers are:

$a,\ a+2,\ a+7,\ a+15$

So, the difference between the largest and smallest numbers:

$= (a + 15) - a = 15$

Hence, the correct answer is $15$.

Q.2) In an examination, the average mark of 4 girls and 6 boys is 24. Each of the girls has the same marks while each of the boys has the same marks. If the marks of any girl are at most double the marks of any boy, but not less than the marks of any boy, then the number of possible distinct integer values of the total marks of 2 girls and 6 boys is:

A) 19

B) 21

C) 20

D) 22

Solution:-

Let the marks of a boy be $x$ and that of a girl be $y$.
So, $4y + 6x = 240$
Also, $x ≤ y ≤ 2x$.
If $x = y$, then $4x + 6x = 240 ⇒ x = 24$ and $y = 24$
So, $2y + 6x = 192$
If $y = 2x, 8x + 6x = 240 ⇒ x = 17.14$ and $y = 34.28$
So, $2y + 6x = 171.41$
So, $171.41 ≤ 2y + 6x ≤ 192$
There will be 21 integer values in between.
Hence, the correct answer is option (2).

Q.3) The average of three integers is 13. When a natural number n is included, the average of these four integers remains an odd integer. The minimum possible value of n is:

A) 3

B) 4

C) 5

D) 6

Solution:-

It is given that the average of three numbers is 13.
Sum = 3 × 13 = 39
It is given, $\frac{39+n}{4}$ is a odd number.
Minimum value $\frac{39+n}{4}$ can take such that n is a natural number is 11
$\frac{39+n}{4}$=11
n = 5
Hence, the correct answer is 5.

Question Type 5: Based on Profit and Loss

Topic: Profit and Loss

Key concept used: Profit or Loss%, Discount%

Profit and Loss has a variety of questions. You will find the question on the concept including profit%, loss%, discount%, relating CP and SP, relating MP and SP, number of articles sold, etc.

Key Concept and Formula:

1. Profit Percentage: It is calculated on CP (Cost Price).

Profit % = $\frac {Profit}{CP} × 100 \%$

2. Loss Percentage: It's also calculated on CP (Cost Price).

Loss % = $\frac {Loss}{CP} × 100 \%$

3. Discount Percentage: It's calculated on MP (Marked Price).

Discount % = $\frac {Discount}{MP} × 100 \%$

Previous Years' Questions Based on Profit and Loss

Q.1) The selling price of a product is fixed to ensure $40 \%$ profit. If the product had cost $40 \%$ less and had been sold for 5 rupees less, then the resulting profit would have been $50 \%$. The original selling price, in rupees, of the product is

A) 15

B) 20

C) 12

D) 10

Solution:-

Let the cost price be $x.$
Then selling price = $x + 40\% \text{ of } x = x + 0.4x = 1.4x$
Now, new cost price = $x - 40\% \text{ of } x = x - 0.4x = 0.6x$
New selling price = $1.4x - 5$

Given: profit in new case = $50\%$ of new cost price = $0.6x \times 0.5 = 0.3x$
So, New selling price = $0.6x + 0.3x=0.9x$
So, $1.4x - 5 = 0.9x$
$⇒1.4x - 0.9x = 5 \Rightarrow 0.5x = 5 \Rightarrow x = 10$
Original selling price = $1.4x = 1.4 \times 10 = 14$

Hence, the correct answer is option 4.

Q.2) Gita sells two objects A and B at the same price such that she makes a profit of 20% on object A and a loss of 10% on object B. If she increases the selling price such that objects A and B are still sold at an equal price and a profit of 10% is made on object B, then the profit made on object A will be nearest to:

A) 42%

B) 47%

C) 45%

D) 46%

Solution:-

Let the original selling price of both A and B be Rs 100.
So, the cost price of A (Profit of 20%) = $\frac{5}{6} \times 100 = \frac{250}{3}$
And, Cost price of B (Loss of 10%) = $\frac{10}{9} \times 100 = \frac{1000}{9}$
After an increase in the selling price by some value, the profit on object B is 10%.
So, the new selling price = 110% of the cost price of B
= $\frac{1000}{9} \times \frac{110}{100} = \frac{1100}{9}$
Profit of A = $\frac{1100}{9} - \frac{250}{3} = \frac{350}{9}$
Profit percentage of A = $\frac{\frac{350}{9}}{\frac{250}{3}} \times 100 = 46.67$% (Nearest to 47%)
Hence, the correct answer is option (2).

Q.3) Ankita buys 4 kg cashews, 14 kg peanuts and 6 kg almonds when the cost of 7 kg cashews is the same as that of 30 kg peanuts or 9 kg almonds. She mixes all the three nuts and marks a price for the mixture in order to make a profit of Rs.1752. She sells 4 kg of the mixture at this marked price and the remaining at a 20% discount on the marked price, thus making a total profit of Rs. 744. Then the amount, in rupees, that she had spent in buying almonds is:

A) 1680

B) 1176

C) 2520

D) 2530

Solution:-

It is given,7C = 30P = 9A and Ankita bought 4C, 14P and 6A.
Let 7C = 30P = 9A = 630k
C = 90k, P = 21k, and A = 70k
Cost price of 4C, 14P and 6A = 4(90k)+14(21k)+6(70k) = 1074k
Marked up price = 1074k + 1752
$\begin{aligned} & \text { S.P }=\frac{1}{6}(1074 k+1752)+\left(\frac{4}{5}\right)\left(\frac{5}{6}\right)(1074 k+1752)=\frac{5}{6}(1074 k+1752) \\ & \text { S.P-C.P }=\text { profit } \\ & 1460-\frac{1074 k}{6}=744 \\ & \frac{1074 k}{6}=716\end{aligned}$
k = 4
Money spent on buying almonds = 420k = 420 × 4 = Rs 1680
The correct answer is Rs. 1680.

Conclusion

The CAT Quantitative Aptitude section for CAT is very vast but if you analyse the previous year’s question paper of CAT, you will find the QA CAT important topics revolve around few core concepts Like

• Arithmetic: Percentage, Profit and Loss, SI and CI, TSD, Time and Work, Average and Mixture

• Number Systems: Factors, Divisibility, Remainders, HCF and LCM

• Algebra: Function, Equations, Inequalities

• Geometry: Triangles, Angles, Polygons

• Modern Maths: Sequence and Series, Logarithmic, Permutation and Combination

Mastering these areas not only improves accuracy but also ensures that you don’t miss out on the most high-yield questions. A focused approach—solving past CAT papers, practicing variations within these types, and learning quick shortcuts—can give you a clear edge.

Best resources & practice material for CAT Algebra

1. Arun Sharma: A Quantitative Approach for CAT (7th Edition)
2. Quantitative Aptitude for CAT by Nishit K Sinha

CAT 2025 Preparation Resources by Careers360

The candidates can download the various CAT preparation resources designed by Careers360 using the links given below.