CAT 2025 Algebra Decoded: 4 Equation Types That Appear Year After Year

Introduction to CAT Algebra in Quantitative Aptitude

Algebra has numerous topics and concepts. It focuses on functions, equations, inequalities, modulus, etc. It helps us to build a strong foundation and carries a significant weightage in the CAT exam. Algebra in CAT will certainly boost your CAT percentile in the quant section.

Why Algebra dominates CAT Quant every year?

Algebra is the most dominant topic in the quantitative aptitude section of CAT and other MBA entrance exams. Why is it so?
The answer lies within its consistency over the past few years. Algebra has the highest weightage among the others in CAT. Apart from direct questions from algebra, it acts as an important tool to solve the questions of other domain like Arithmetic, logarithm, surds and exponents, and Modern Mathematics.

Must-know Algebra concepts for CAT candidates

We have analysed the last 5 years of CAT question papers to give you some insight on the concepts that have been asked previously, as listed below:

Overview of Algebra in the CAT Exam

Algebra in the CAT exam forms a key part of the Quantitative Ability section, testing concepts like equations, inequalities, sequences, and functions. Mastery of these topics helps in solving problems quickly and accurately, boosting overall CAT 2025 performance.

Weightage of Algebra in CAT Quant section

As seen in previous years, here is a summary (year-wise and slot-wise) of the number of questions asked from Algebra in CAT

Why mastering equations is the game-changer

As we have seen that every year, on average, 3 to 4 questions are asked from equations. Equations can be linear, quadratic, or miscellaneous. Mastering these equations can be the game-changer in CAT-2025 as it comprises of healthy weightage in the quantitative aptitude section.

Apart from this, solving equations mainly focuses on finding the value or the range of values of the unknown variable. These questions have a lower possibility of being wrong. Also, practising these questions will help in developing critical and analytical thinking.

Type 1 – Linear Equations in CAT Algebra

Linear equations can be in one dimension, two dimensions or three dimensions. Linear equations are a fundamental topic in CAT Algebra, involving equations of the first degree with one or more variables. These questions test your ability to solve for unknowns efficiently and form the basis for more complex problem-solving.

Standard forms and solving strategies

Linear equations in two variables (x and y) are typically presented in the form

ax + by + c = 0,

where 'a' and 'b' are non-zero coefficients and 'c' is a constant.

Solving Linear Equations:

If there are two sets of linear equations, such as $a_1x+b_1y+c_1=0$ and $a_2x+b_2y+c_2=0$,

The solutions of these equations can be determined by different methods:

1. Graphical Method

2. Elimination Method

3. Substitution method.

Tricks to handle multiple variables quickly

To quickly solve questions having two or more variables, you should apply the method of

1. Elimination

2. Substitution, to reduce the larger equations in to simpler ones or you should apply trial and error methods to solve through options.

3. For two linear equations, $a_1x + b_1y + c_1 = 0$
and $a_2x + b_2y + c_2 = 0$

Example CAT Algebra questions on linear equations

Example 1: For some real numbers $a$ and $b$, the system of equations $x +y = 4$ and $(a+5)x + (b^2 -15)y = 8b$ has infinitely many solutions for $x$ and $y$. Then, the maximum possible value of $ab$ is: [CAT 2023, slot 3]

Solution:

For the given equations:
$x +y = 4$ and $(a+5)x + (b^2 -15)y = 8b$
Condition for infinite many solutions
$\frac {1}{a+5} = \frac {1}{ b^2 -15} =\frac {4}{8b}$
Solving $\frac {1}{ b^2 -15} =\frac {4}{8b}$
$⇒ 8b=4(b^2-15)$
On solving this quadratic equation, we get $b = -3, 5$.
Solving $\frac {1}{ a+5} =\frac {4}{8b}$
⇒ 8b = 4(a+5)
For b = -3, a = -11 and hence, $ab = (-3) \times (-11) = 33$
For $b = 5, a = 5$ and hence, $ab = (5) \times (5) = 25$
So, the maximum value of $ab$ is 33.

Example 2: The number of distinct integer solutions $(x, y)$ of the equation $|x+y|+|x-y|=2$, is [CAT 2024, slot 3]

Solution:

We’ll analyze all integer pairs $(x, y)$ such that the equation holds.

Let’s denote:
$A = |x + y|$; $B = |x - y|$

We are told: $A + B = 2$
Since both $A$ and $B$ are non-negative and integers, possible values of $(A, B)$ are: $(0, 2)$, $(1, 1)$, and $(2, 0)$

Let’s find all integer solutions $(x, y)$ for each case.

Case 1: $|x + y| = 0$ and $|x - y| = 2$

Then $x + y = 0$ and $x - y = \pm 2$

Solving:

• $x + y = 0$, $x - y = 2$
  Solving: $x = 1$, $y = -1$
• $x + y = 0$, $x - y = -2$
  Solving: $x = -1$, $y = 1$

So, 2 solutions.

Case 2: $|x + y| = 1$ and $|x - y| = 1$

Then $x + y = \pm 1$, $x - y = \pm 1$

Possible combinations:

1. $x + y = 1$, $x - y = 1$
   Solving: $x = 1$, $y = 0$
2. $x + y = 1$, $x - y = -1$
   Solving: $x = 0$, $y = 1$
3. $x + y = -1$, $x - y = 1$
   Solving: $x = 0$, $y = -1$
4. $x + y = -1$, $x - y = -1$
   Solving: $x = -1$, $y = 0$

So, 4 solutions.

Case 3: $|x + y| = 2$, $|x - y| = 0$

Then $x - y = 0$, $x + y = \pm 2$

Solving:

• $x - y = 0$, $x + y = 2$
  $x = y$, so $2x = 2 \Rightarrow x = y = 1$
• $x - y = 0$, $x + y = -2$
  $x = y$, so $2x = -2 \Rightarrow x = y = -1$

So, 2 more solutions.

• Case 1: 2 solutions
• Case 2: 4 solutions
• Case 3: 2 solutions

Total distinct integer solutions: $8$

Hence, the correct answer is $8$.

Type 2 – Quadratic Equations in CAT Algebra

Quadratic equations in CAT Algebra involve second-degree equations with one or more variables. Questions on this topic assess your skills in factorization, applying the quadratic formula, and analyzing roots for problem-solving.

An equation of the form $ax^2+bx+c=0$ where a, b, and c are all real and a is not equal to 0, is a quadratic equation.

Key quadratic identities for CAT

There are a few quadratic identities which are frequently used:
1. Difference of Squares: a² - b² = (a + b)(a - b).

2. Square of a Binomial: (a + b)² = a² + 2ab + b².

3. Square of a Binomial: (a - b)² = a² - 2ab + b².

Approaches to solving quadratic equations

There are a few approaches to solving the quadratic equation:

1. Quadratic Formula (Shridharacharya Formula)

For an equation of the form

$ax^2+bx+c=0$

$x = \frac{-b \pm \sqrt{D}}{2a}$ where $D= b^2-4ac$

Example: Find the roots of $5x^2+8x+3=0$

Solution:

Here

$a=5, b= 8, c =3$

Discriminant, $D=8^2-4 \times 5 \times 3=4$

So, $x= \frac{-8 \pm \sqrt{4}}{10}$
$x=\frac{-3}{5}, -1$

2. Method of splitting middle term:

Example: Find the roots of $5x^2+8x+3=0$

Solution:

$5x^2+8x+3=0$

⇒ $5x^2+5x+3x+3=0$

⇒ $5x(x+1)+3(x+1)=0$

⇒ $(x+1)(5x+3)=0$

⇒ $x = -1, \frac{-3}{5}$

Common traps and shortcuts in CAT Quant

While solving a quadratic equation, a student can make mistakes in

• misinterpreting the questions

• making calculation errors

• While finding discriminants, students often neglect the negative value of the discriminant, which leads to a wrong answer. You must consider each possibility.

Some important points that may help you to solve questions based on quadratic equations effectively:

(i) If D is a perfect square, then the roots are rational and in case it is not a perfect square then the roots are irrational.

(ii) In the case of imaginary roots (D < 0) and if p + iq is one root of the quadratic equation, then the other must be the conjugate p - iq and vice versa (where p and q are real and $i = \sqrt{-1}$)

(iii) For an equation of the form

$ax^2+bx+c=0$

If a > 0, D < 0, roots are imaginary.

If a > 0, D = 0, roots are real and identical.

If a > 0, D > 0, roots are real and distinct.

If a < 0, D > 0, roots are imaginary.

If a < 0, D > 0, roots are real and distinct.

If a < 0, D = 0, roots are real and equal.

(iv) For an equation of the form

$ax^2+bx+c=0$

Sum of roots = $\frac{-b}{a}$

Product of roots = $\frac{c}{a}$

Sample questions and solutions

Q.1) If r is a constant such that |x² - 4x - 13| = r has exactly three distinct real roots, then the value of r is:

A) 17

B) 21

C) 15

D) 15

Solution:-

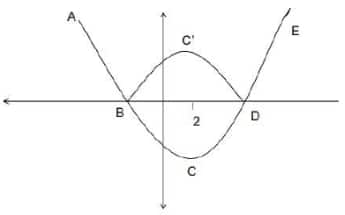
Alternatively,$|x^2−4x−13|=r$.
This can be represented in two parts:
$x^2-4x-13=r$ if r is positive.
$x^2-4x-13=-r$ if r is negative.
Considering the first case: $x^2−4x−13=r$
The quadratic equation becomes: $x^2−4x−13−r=0$
The discriminant for this function is : $b^2−4ac=16−[4×(−13−r)]=68+4r$
Since r is positive, the discriminant is always greater than 0 this must have two distinct roots.
For the second case:
$x^2−4x−13+r=0$ the function inside the modulus is negative.
The discriminant is $16−(4×(r−13))=68−4r$
In order to have a total of 3 roots, the discriminant must be equal to zero for this quadratic equation to have a total of 3 roots.
So, $68−4r=0$
⇒ $r=17$
For $r=17$, we can have exactly 3 roots.

Hence, the correct answer is option (1).

Q.2) Suppose one of the roots of the equation $ax^2−bx+c=0$ is $2+3i$, Where a,b and c are rational numbers and a≠0. If $b=c^3$ then |a| equals

A) 1

B) $\frac{2}{13\sqrt{13}}$

C) 3

D) $\frac{2}{13}$

Solution:-

Given one root $x=2+3i$ and a,b,c∈Q,a≠0

Since coefficients are rational, the other root is $2−3i$

Sum of roots: $(2+3i)+(2−3i)=4=\frac{b}{a$

⇒ $b=4a$

Product of roots: $(2+3i)(2−3i)=4+9=13$

⇒ $\frac{c}{a} =13$
⇒ $c =13a$

Given $b=c^3$
⇒ $4a=2197a^3$
⇒ $a=\frac{2}{13\sqrt{13}}$

Hence, the correct answer is option 2.

Q.3) If the equations $x^2+mx+9=0,x^2+nx+17=0$ and $x^2+ (m+n)x+35=0$ have a common negative root, then the value of $(2m+3n)$ is

Solution:-

Let the common negative root be x

Since x is a root of all three equations:

From first equation: $x^2+mx+9=0$
From second equation: $x^2+nx+17=0$
From third equation: $x^2+(m+n)x+35=0$

Subtract the second from the first:
$(x^2+mx+9)−(x^2+nx+17)=0$
⇒ $(m−n)x−8=0$
So, $(m−n)x=8$ ...(i)

Now subtract the third from the first:
$(x^2+mx+9)−(x^2+(m+n)x+35)=0$
⇒$−nx−26=0$
So, $−nx=26⇒nx=−26$ ...(ii)

Add (i) and (ii)
We get, $(m−n)x+nx=8−26⇒mx=−18$ ...(iii)

Now from (ii): $x=−26/n$
Substitute into (iii):
$m⋅(−26/n)=−18$
⇒$−26m=−18n$
⇒$13m=9n$

So, $m/n=9/13$

Let $m=9k, n=13k$

Then $2m+3n=2(9k)+3(13k)=18k+39k=57k$

We now use the value of x from earlier:
From $nx=−26$,
⇒ $13k⋅x=−26⇒x=−2k$

Now substitute $x=−2k$ into the first equation:
$x^2+mx+9=0$
⇒ $(−2k)^2+9k⋅(−2k)+9=0$
⇒ $4k^2−18+9=0$
⇒ $4k^2=9$
⇒ $k^2=4/9⇒k=2/3$

So, $2m+3n=57k=57⋅(2/3)=38$

Q.4) If $(x+6\sqrt2)^{1/2}−(x−6\sqrt2)^{1/2}=2\sqrt2$, then x equals

Solution:-

Given: $(x+6\sqrt2)^{1/2}−(x−6\sqrt2)^{1/2}$
Squaring both sides
$x+6\sqrt2+x−6\sqrt2−2((x+6\sqrt2)(x−6\sqrt2))^{1/2}=8$
⇒ $2x−2(x^2−72)^{1/2}=8$
⇒ $x−(x^2−72)^{1/2}=4$
⇒ $x−4=(x^2−72)^{1/2}$

Squaring both sides again
⇒ $(x−4)^2=x^2−72$
⇒ $x^2+16−8x=x^2−72$
⇒ $x=11$

Hence, the correct answer is 11.

Type 3 – Inequalities and Modulus Equations

Two real numbers or two algebraic expressions related by the symbol > (“Greater Than”) or < (“Less than”) (and by the signs ≥ or ≤) form an inequality.

The inequality consists of two sides, ie. LHS and RHS. LHS and RHS can be algebraic expressions or they can be numbers. The expressions in LHS and RHS have to be considered on the set where LHS and RHS have sense simultaneously. This set is called the set of permissible values of the inequality.

If two or several inequalities contain the same sign (< or >) then they are called inequalities of the same sense. Otherwise, they are called inequalities of the opposite sense.

Now let us consider some basic definitions about inequalities.

For 2 real numbers a and b

The inequality a > b means that the difference a – b is positive.

The inequality a < b means that the difference a – b is negative.

Modulus equations involve an expression with absolute values (e.g., |x|). |always gives a positive value. You require the solutions where the expression inside the modulus is equal to the positive or negative value of the number on the other side of the equation.

For example, |x| = 2 gives x = 2 or – 2.
To solve a basic modulus equation like |ax + b| > c, two equations will be formed
ax+b>c and ax+b<−c, then solve each for x to find the solutions.

Must-know concepts: inequalities & absolute values

Points to remember:

• The inequality a≥b means that a>b or a=b, that is, a is not less than b.

• The inequality a≤b means that a<b or a=b, that is, a is not greater than b.

Notation of Ranges:

1. Ranges where the ends are excluded:

If the value of x is denoted as (1, 2) it means 1 < x < 2 i.e. x is greater than 1 but smaller than 2.

Similarly, if we denote the range of values of $x$ as (-9, 1) U (8, 23), this means that the value of $x$ can be denoted as -9 < x < 1 and 8 < x < 23.

2. Ranges where the Ends are Included

[2, 5] means $2 \leq x \leq 5$

3. Mixed ranges

(3, 21] means $3 < x \leq 21$

Solving Algebra inequalities in less time

You can use the following results to solve inequalities in less time:

1. $a^2 +b^2 \geq 2ab$
2. $|a+b| \leq |a| + |b|$
3. $|a-b| \geq |a| - |b|$
4. Arithmetic mean ≥ Geometric mean.

$\frac{a+b}{2} \geq \sqrt {ab}$

5. $\frac{a}{b}+\frac{b}{a} \geq 2$ if $a>0$ and $b>0$ or if $a<0$ and $b<0$.
6. $a^2+b^2+c^2 \geq ab+bc+ca$
7. $(a+b)(b+c)(c+a) \geq 8abc$ if $a \geq 0, b \geq 0$ and $c \geq 0$, the equation being obtained when $a=b=c$.
8. If $a+b=2$, then $a^4+b^4 \geq 2$

CAT-level practice questions with solutions

Q.1) The number of integers n that satisfy the inequalities |n – 60| < |n – 100| < |n – 20| is:

A) 21

B) 19

C) 18

D) 18

Solution:-

Given: |n – 60| < |n – 100| < |n – 20|

The distance between these two points can be represented by |x – y| or |y – x|.

Let's take the first part of the inequality
|n – 60| < |n – 100|
This inequality holds good for the values of n below 80.
Hence ‘n’ should be less than 80.

Now Let's check for the later part of the inequality.
|n – 100| < |n – 20|
This inequality holds good for the values of n above 60.
Hence ‘n’ should be greater than 60.

∴ Values of ‘n’ range from 61 to 79.
So, the total possible integers that satisfy this inequality are 19.

Hence, the correct answer is 19.

Q.2) All the values of x satisfying the inequality 1x+5≤12x−3 are

A) −5<x<32 or 32<x≤8

B) x<−5 or x>32

C) x<−5 or 32<x≤8

D) x<−5 or 32<x≤8

Solution:-

Given: 1x+5≤12x−3

⇒2x−3≤x+5

⇒x≤8

But x≠−5 and x≠32 as at these values fractions are not defined.

So, the set of solutions becomes

x<−5 or 32<x≤8

Hence, the correct answer is option 3.

Q.3) If x and y satisfy the equations |x|+x+y=15 and x+|y|−y=20, then (x−y) equals

A) 15

B) 10

C) 20

D) 20

Solution:-

We are given the equations:

|x|+x+y=15−−−−−−−(1)
x+|y|−y=20−−−−−−−−−−(2)

There are 4 cases:

Case 1: Both x and y are positive
Then the equations become
x+x+y=15⇒2x+y=15
and x+y−y=20⇒x=20
So, y=15−40=−25 which is contradictory. So, this is not possible.

Case 2: x>0 and y<0 are positive
Then the equations become
x+x+y=15⇒2x+y=15
and x−y−y=20⇒x−2y=20
So, 4x+2y+x−2y=30+20⇒x=10
and y=−5
So, x−y=10−(−5)=15

Case 3: Both x and y are negative
Then the equations become
−x+x+y=15⇒y=15 which is contradictory. So, this is not possible.

Case 4: x<0 and y>0
Then the equations become
−x+x+y=15⇒y=15
and x+y−y=20⇒x=20 which is contradictory. So, this is not possible.

From Case 2: x−y=15

Hence, the correct answer is option 1.

Q.4) The number of distinct real values of x, satisfying the equation max{x,2}−min{x,2}=|x+2|−|x−2|, is

Solution:-

We are given the equation:max{x,2}−min{x,2}=|x+2|−|x−2|

Left-hand side: max{x,2}−min{x,2}=|x−2|
(since difference of max and min of two numbers is just their absolute difference)

So, the equation becomes:

|x−2|=|x+2|−|x−2|

Bring all terms to one side:

2|x−2|=|x+2|

Case 1: x≥2

Then |x−2|=x−2, |x+2|=x+2

The equation becomes:

2(x−2)=x+2⇒2x−4=x+2⇒x=6

This is valid for x≥2

Case 2: −2≤x<2

Then |x−2|=2−x, |x+2|=x+2

⇒2(2−x)=x+2⇒4−2x=x+2⇒3x=2⇒x=23

This is valid in [−2,2)

Case 3: x<−2

Then |x−2|=2−x, |x+2|=−x−2
⇒2(2−x)=−x−2⇒4−2x=−x−2⇒−x=−6⇒x=6

But x=6 does not lie in x<−2, so discard this solution.

Thus, valid real solutions are:

x=6 and x=23

There are 2 distinct real values.

Hence, the correct answer is 2.

Type 4 – Functions & Polynomials in CAT Algebra

Functions and polynomials in CAT Algebra focus on understanding expressions, relationships, and transformations.

Polynomials:

A polynomial is an expression in x or other variable which may contain one or more terms. Also, the power of the variable should be a whole number.

The degree of a polynomial: It is the highest power of the variable in that polynomial.

It is important to note that the degree of a polynomial can never be negative and it should be a non-negative integer.

For instance, in the polynomial $5x^3−2x^2+3x−7$, the degree is 3, because the highest power of x is 3.

Introduction to Functions:

A function is a relation between a set of inputs and a set of possible outputs where each input is related to exactly one output. The set of inputs is called the domain and the set of possible outputs is called the codomain.

Notation:

A function f from set A to set B is denoted by f: A ➔ B.

Understanding functions and graph-based questions

Graph of some important functions:

Function of a Function (Composite Function)

A composite function is the function of another function. If f is a function from A in to B and g is a function from B in to C, then their composite function denoted by (gof) is a function from A in to C defined by

gof (x) = g[f(x)]

Also, composite function fog (read as "f of g") is defined as:

fog (x) = f[g(x)]

Q.1) A function f maps the set of natural numbers to whole numbers, such that $f(xy)=f(x)f(y)+f(x)+f(y)$ for all x,y and $f(p)=1$ for every prime number p. Then, the value of $f(160000)$ is

A) 8191

B) 2047

C) 4095

D) 4096

Solution:-

Given: $f(xy)=f(x)f(y)+f(x)+f(y)$ for all x,y∈N
And $f(p)=1$ for every prime p

Let’s find $f(160000)$
Note: $160000=16×10000=(2^4)×(10^4)=2^4×(2×5)^4=2^8×5^4$

Let’s try to find a pattern.

Since $f(p) =1$, So $f(2)=1$
$f(4)=f(2×2)=f(2)f(2)+f(2)+f(2)=1+1+1=3$
$f(8)=f(2×4)=f(2)f(4)+f(2)+f(4)=3+1+3=7$
$f(16)=f(2×8)=f(2)f(8)+f(2)+f(8)=7+1+7=15$
Similarly, $f(2^8)=f(256)=255$

Also, $f(5)=1$
$f(25)=f(5×5)=f(5)f(5)+f(5)+f(5)=1+1+1=3$
$f(125)=f(5×25)=f(5)f(25)+f(5)+f(25)=3+1+3=7$
Similarly, $f(5^4)=f(625)=15$

Now, $f(160000)=f(2^8×5^4)=f(2^8)f(5^4)+f(2^8)+f(5^4)$
$=255×15+255+15$
$=3825+255+15$
$=4095$

Hence, the correct answer is option 3.

Q.2) For any non-zero real number $x$, let $f(x)+2f(1/x)=3x$. Then, the sum of all possible values of $x$ for which $f(x)=3$, is

A) -2

B) 2

C) -3

D) 3

Solution:-

We are given:
$f(x)+2f(1/x)=3x$−−−−−−−−(1)
Also, we are told: $f(x)=3$

Substituting into (1):
$3+2f(1/x)=3x⇒f(1/x)=(3x−3)/2$−−−−−−−−(2)

Now use (1) again but switch $x$ with $1/x$:
$f(1/x)+2f(x)=3x$
Substitute $f(x)=3$:
$f(1/x)+6=3x⇒f(1/x)=3x−6$−−−−−−(3)

Equating (2) and (3):
$(3x−3)/2=3x−6$

Multiply both sides by 2:
$3x−3=6x−12$

Bring all terms to one side:
$3x+9−6x=0$

Multiply through by x:
$3x^2+9x−6=0$

Divide by 3:
$x^2+3x−2=0$

Sum of all possible values of $x=-3$.

Hence, the correct answer is option 3.

Q.3) Let a, b, and c be non-zero real numbers such that $ b^2 <4ac$, and $f(x)=ax^2+bx+c$. If the set S consists of all integers m such that f(m) < 0, then the set S must necessarily be:

A) the set of all positive integers

B) the set of all integers

C) either the empty set or the set of all integers

D) either the empty set or the set of all integers

Solution:-

It is given that $f(x)=ax^2+bx+c$ and $b^2<4ac$
This means that f(x) has imaginary roots and therefore, no real roots at all.
If a function has no real roots, the graph of the function can never touch the x-axis, because touching the x-axis means, for some real value of x, the value of f(x) is 0. This means that the function has roots in some real value of x.
When we graph this quadratic function f(x), we get a parabola that should never touch the x-axis.
Such a parabola should be completely above the x-axis or completely below the x-axis.

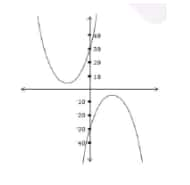
If it is completely above the x-axis:
● It means that the value of f(x) is always positive for any value of x.
The set of values of x that satisfies the condition that f(x) < 0 is an empty set.
● If it is completely below the x-axis:
It means that the value of f(x) is always negative for any value of x.
The set of values of x that satisfies the condition that f(x) < 0 is the set of all real numbers.
Since Set S contains all the integers ‘m’ that satisfy the above conditions,
So, set S is either an empty set or the set of all integers.
Hence, the correct answer is option (3).

Q.4) Let $0≤a≤x≤100$ and $f(x)=|x−a|+|x−100|+|x−a−50|$. Then the maximum value of f(x) becomes 100 when a is equal to:

A) 25

B) 100

C) 50

D) -50

Solution:-

$x≥a$,
so, $|x−a|=x−ax<100$,
so $|x−100|=100−xf(x)=(x−a)+(100−x)+|x−a−50|=100⇒|x−a−50|=a$

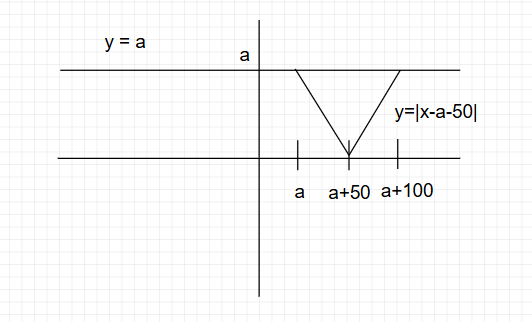
From the graph, we can see that when x = a
Then,
$|x - a - 50| = a$
$⇒ a = 50$
Similarly when $x = a + 100$
$|x – a - 50|= a$
$⇒ a = 50$
So, the value of a is 50 when f(x) is 100.

Hence, the correct answer is option (3).

High-frequency CAT Algebra problems on polynomials

Questions on Polynomials that are asked in CAT mainly based on following concepts:

• Sum of zeros and product of zeros

1. Sum of Zeroes (α and β): For a quadratic polynomial $ ax^2+bx+c$, the sum of its zeroes (roots) is given by $\frac {-b}{a]$.

For a cubic polynomial (zeros α, β and γ) $ ax^3+bx^2+cx+d$, the sum of its zeroes (roots) is given by $\frac {-b}{a]$.

2. Product of Zeroes:

For a quadratic polynomial $ ax^2+bx+c$, the product of its zeroes (roots) is given by $\frac{c}{a}$.

For a cubic polynomial $ ax^3+bx^2+cx+d$, the product of its zeroes (roots) is given by $\frac {-d}{a]$.

Also, for cubic polynomial (zeros α, β and γ)

αβ +βγ + γα = c/a

• Questions based on factor theorem:

Factorization (Factor theorem)

If a polynomial P(x) has a factor (x -a), then P(a) = 0 and conversely, if P(a) = 0 then (x -a) is a factor of P(x). This is the factor theorem.

Q.1) $f(x)=(x^2+2x−15)(x^2−7x−18)$ is negative if and only if

A) $−5<x<−2$ or $3<x<9$

B) $−2<x<3$ or $x>9$

C) $x<−5$ or $−2<x<3$

D) $x<−5$ or $−2<x<3$

Solution:-

$f(x)=(x^2+2x−15)(x^2−7x−18)$
$⇒f(x)=(x+5)(x−3)(x−9)(x+2)<0$
We have four inflection points −5,−2,3, and 9 .
For $x<−5$, all four terms (x+5),(x−3),(x−9),(x+2) will be negative.

The overall expression will be positive.
Similarly, when $x>9$, all four terms will be positive.
When x belongs to $(−2,3)$, two terms are negative and two are positive.

The overall expression is positive again.
We are left with the range $(−5,−2)$ and $(3,9)$ where the expression will be negative.

Thus, the correct answer is option 1) $−5<x<−2$ or $3<x<9$.

Q.2) The roots $\alpha, \beta$ of the equation $3 x^2+\lambda x-1=0$, satisfy $\frac{1}{\alpha^2}+\frac{1}{\beta^2}=15$. The value of $\left(\alpha^3+\beta^3\right)^2$, is

A) 1

B) 4

C) 9

D) - 9

Solution:-

Given: $\frac{1}{\alpha^2} + \frac{1}{\beta^2} = 15$

We know: $\frac{1}{\alpha^2} + \frac{1}{\beta^2} = \frac{\alpha^2 + \beta^2}{\alpha^2 \beta^2}$

From the equation $3x^2 + \lambda x - 1 = 0$,
sum of roots $\alpha + \beta = -\frac{\lambda}{3}$, product of roots $\alpha \beta = -\frac{1}{3}$
So, $\alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta = \left(\frac{\lambda^2}{9}\right) + \frac{2}{3}$

Also, $\alpha^2 \beta^2 = (\alpha \beta)^2 = \left(\frac{1}{9}\right)$

Now,
$\frac{\alpha^2 + \beta^2}{\alpha^2 \beta^2} = 15$
$\Rightarrow \left(\frac{\lambda^2}{9} + \frac{2}{3} \right) \div \frac{1}{9} = 15$
$\Rightarrow 9\left( \frac{\lambda^2}{9} + \frac{2}{3} \right) = 15$
$\Rightarrow \lambda^2 + 6 = 15 \Rightarrow \lambda^2 = 9 \Rightarrow \lambda = \pm 3$

Now, $\alpha^3 + \beta^3 = (\alpha + \beta)^3 - 3\alpha\beta(\alpha + \beta)$

We have: $\alpha + \beta = -\frac{\lambda}{3} = \pm 1$, $\alpha\beta = -\frac{1}{3}$

Case 1: $\alpha + \beta = - 1$

$\alpha^3 + \beta^3 = (-1)^3 - 3\left(-\frac{1}{3}\right)(-1) = -1 - 1 = -2$

We get, $(\alpha^3 + \beta^3)^2 = (-2)^2 = 4$

Case 2: $\alpha + \beta = 1$

$\alpha^3 + \beta^3 = (1)^3 - 3\left(-\frac{1}{3}\right)(1) = 1 + 1 = 2$

We get, $(\alpha^3 + \beta^3)^2 = (2)^2 = 4$

Hence, the correct answer is option 2.

Q.3) If $x$ and $y$ are real numbers such that $4 x^2+4 y^2-4 x y-6 y+3=0$, then the value of $(4 x+5 y)$ is

Solution:-

Given:
$4x^2 + 4y^2 - 4xy - 6y + 3 = 0$

$⇒4x^2 + y^2 - 4xy +3y^2- 6y + 3 = 0$

$⇒(2x-y)^2+3(y^2- 2y + 1) = 0$

$⇒(2x-y)^2+3(y-1)^2 = 0$

This is possible if and only if $2x=y$ and $y=1$
So, $x= \frac12$

Now, compute $4x + 5y = 4 \cdot \frac{1}{2} + 5 \cdot 1 = 2 + 5 = 7$

Hence, the correct answer is $7$.

How to simplify and solve faster
To simplify the questions on polynomial, you should learn few identities and try to solve through options.

Listed below are the formulas of algebraic expressions.

1. $(a+b)^2=a^2+2ab+b^2$

2. $(a-b)^2=a^2-2ab+b^2$

3. $a^2-b^2=(a+b)(a-b)$

4. $a^3+b^3=(a+b)(a^2-ab+b^2 )$

5. $a^3-b^3=(a-b)(a^2+ab+b^2 )$

6. $(a+b)^3=a^3+3a^2 b+3ab^2+b^3$

7. $(a-b)^3=a^3-3a^2 b+3ab^2-b^3$

8. $(a + b + c)^2= a^2+ b^2+ c^2+ 2ab + 2bc + 2ca$

9. $a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$. If (a + b + c) = 0, then $a^3+b^3+c^3=3abc$.

Advanced CAT Algebra Problem Types

Advanced CAT algebra problems involve:

• Logarithm with equations

• Sequence and Series with equations and logarithm

• Minimum and maximum value of a function

• Equations involving ratios

• Equations involving ages

• Complex problems of algebra with geometry

Advanced CAT Algebra questions involving two or more concepts

We will understand how algebra is integrated with the ratios and proportions with the help of the following examples:

Q.1) If $5-\log _{10} \sqrt{1+x}+4 \log _{10} \sqrt{1-x}=\log _{10} \frac{1}{\sqrt{1-x^2}}$, then find the value of $100x$?

A) 99

B) $\frac{99}{100}$

C) 110

D) 110

Solution:-

$5-\log _{10} \sqrt{1+x}+4 \log _{10} \sqrt{1-x}=\log _{10} \frac{1}{\sqrt{1-x^2}}
$
We can re-write the equation as:
$⇒5-\log _{10} \sqrt{1+x}+4 \log _{10} \sqrt{1-x}=\log _{10}(\sqrt{1+x} \times \sqrt{1-x})^{-1}$
$
\begin{aligned}
& ⇒5-\log _{10} \sqrt{1+x}+4 \log _{10} \sqrt{1-x}=(-1) \log _{10}(\sqrt{1+x})+(-1) \log _{10}(\sqrt{1-x}) \\
&⇒ 5=\log _{10} \sqrt{1+x}-\log _{10} \sqrt{1+x}-\log _{10} \sqrt{1-x}-4 \log _{10} \sqrt{1-x} \\
& ⇒5=-5 \log _{10} \sqrt{1-x} \\
& ⇒\sqrt{1-x}=\frac{1}{10}
\end{aligned}
$
$⇒(\sqrt{1-x})^2=\frac{1}{100}$
$\therefore \quad x=1-\frac{1}{100}=\frac{99}{100}$

So, $100 x=100 \times \frac{99}{100}=99$

Hence, the correct answer is 99

Q.2) When Rajesh's age was same as the present age of Garima, the ratio of their ages was 3:2. When Garima's age becomes the same as the present age of Rajesh, the ratio of the ages of Rajesh and Garima will become

A) 5:4

B) 4:3

C) 2:1

D) 3:2

Solution:-

Let present ages of Rajesh and Garima be $R$ and $G$ respectively.
When Rajesh's age was $G$, the ratio of their ages was $3:2$.
So, at that time:
$R - G$ years ago, Rajesh's age = $G$, Garima's age = $G - (R - G) = 2G - R$

Given:
$\frac{G}{2G - R} = \frac{3}{2}$

Cross multiplying:
$2G = 3(2G - R)$
$2G = 6G - 3R$
$3R = 4G$
$\Rightarrow R = \frac{4G}{3}$

Now, when Garima's age becomes $R$, the time passed = $R - G = \frac{4G}{3} - G = \frac{G}{3}$
At that time, Rajesh's age = $R + \frac{G}{3} = \frac{4G}{3} + \frac{G}{3} = \frac{5G}{3}$

Required ratio = $\frac{5G/3}{R} = \frac{5G/3}{4G/3} = \frac{5}{4}$

Hence, the correct answer is option 1.

Q.3) A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is

Solution:-

Let the initial number of fruits be $x$ and apples be $y$.

The stock of mangoes is given to be 40% of x, which shows that the number of mangoes will be $\frac{2x}{5}$.

The total number of sold fruits is given by including the selling of all the fruits- mango, apple and banana.

Now, the total no. of fruits sold

$=\frac{2x}{10}+\frac{4y}{10}+96=\frac{x}{2}$

$⇒\frac{x}{5}+\frac{2y}{5}+96=\frac{x}{2}$

On simplifying, we get,

$2x+4y+960=5x$

$⇒x=\frac{960+4y}{3}$

For $x$ to be a positive integer, let us check for values of $y$.

$4y+960$ has to be divisible by $3$, which means $4y$ will also be divisible by $3$.

For $\frac{4y}{10}$ to be an integer, $y$ has to be divisible by $5$.

We can say, that the smallest value of $y$ has to be multiple of both $3$ and $5$, i.e. $15$.

Now, put the value of $y=15$.

We get, $x=\frac{960+4 \times 15}{3}$

$⇒x=\frac{1020}{3}$

$⇒x=340$

So, the smallest possible number of fruits in stock at the starting of the day will be $340$.

Hence, the correct answer is $340$.

Q.4) For natural numbers x, y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is:

A) 34

B) 35

C) 36

D) 38

Solution:-

It is given, y(x + z) = 19
y cannot be 19.
If y = 19, then x + z = 1 which is not possible when both x and z are natural numbers.
Therefore, y = 1 and x + z = 19
It is given, z(x + y) = 51
z can take values 3 and 17.
Case 1:
If z = 3, y = 1 and x = 16
xyz = 3 × 1 × 16 = 48
Case 2:
If z = 17, y = 1 and x = 2
xyz = 17 × 1 × 2 = 34
So, the minimum value xyz can take is 34.
Hence, the correct answer is option (1).

Q.5) The number of integer solutions of the equation $\left(x^2-10\right)^{(x^2-3 x-10)}=1$ is:

A) 4

B) 6

C) 3

D) 8

Solution:-

Case 1: When $x^2-3 x-10=0$ and $x^2-10 \neq 0$

$x^2-3 x-10=0$
$ ⇒(x-5)(x+2)=0$
$\therefore x=5 \text { or }-2
$
Case 2: $x^2-10=1$
$⇒
x^2-11=0
$
$\therefore$ No integer solutions

Case 3: $\mathrm{x}^2-10=-1$ and $\mathrm{x}^2-3 \mathrm{x}-10$ is even.
$x^2-9=0$
$⇒(x+3)(x-3)=0$
$\therefore\mathrm{x}=-3$ or 3
for $\mathrm{x}=-3$ and $+3$, $\mathrm{x}^2-3 \mathrm{x}-10$ is even.

$\therefore$ In total 4 values of $x$ satisfy the equations.

Hence, the correct answer is option (1).

Algebra Important Topics for CAT 2025 & Beyond

Algebra consists of many topics, as discussed earlier in this article. Based on CAT's previous papers analysis, we have divided these topics into two categories:

• High-priority concepts

• Lesser Priority concepts

High-priority concepts based on previous CAT papers

Lesser-seen but tricky Algebra concept

There are a few topics which are less seen but very tricky and important for the CAT exam

• Greatest integer function

• Questions based on the signum function

• Questions involving higher-order polynomials

• Harmonic Progressions

• Questions involving even and odd functions

CAT Algebra Preparation Tips

In this section, we will focus on a few but important tips to prepare for CAT Algebra.

How to build strong basics in Algebra equations

To build a strong foundation, first learn the basic concepts from the NCERT classes 11 and 12. Start with very basic questions and increase the difficulty level gradually.

After learning the basics, apply the concepts in CAT-level questions.

Shortcuts and time-saving tricks for CAT Quant

After building a strong foundation on the topics, the next step is to learn the shortcuts and time-saving techniques. For this, learn some effective calculation methods with the help of Vedic Maths.

Formula sheet for quick revision

Prepare a CAT formula sheet for linear equation, quadratic equation, polynomials, graphs, etc for quick revision.

Best resources & practice material for CAT Algebra

1. Arun Sharma: A Quantitative Approach for CAT (7th Edition)
2. Quantitative Aptitude for CAT by Nishit K Sinha
3. NCERT class 11 and class 12

CAT 2025 Preparation Resources by Careers360

The candidates can download the various CAT preparation resources designed by Careers360 using the links given below.

Common Mistakes in CAT Algebra Preparation

Common mistakes in CAT Algebra preparation include ignoring fundamentals, skipping practice on tricky problems, mismanaging time, and overlooking shortcuts, which can lower accuracy and speed in the exam.

How to Practice Repeated Algebra Questions in CAT

Algebra plays a key role in scoring well in the CAT quantitative aptitude section. I will suggest four-step strategies to practice repeated Algebra questions in CAT.

Step 1: Identify patterns in the last 4 to 5 years of CAT papers and categorise the questions concept-wise.

Step 2: Work on basics, memorise key concepts or tricks, and learn shortcuts.

Step 3: Practice with CAT-specific resources.

Step 4: Evaluate, analyse your mistakes, and focus on weaker areas.