Great Lakes - PGDM & PGPM Admissions 2026
Admissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
How to Crack CAT 2025 QA by Covering 30% syllabus
Upcoming Event
CAT Admit Card Date:05 Nov' 25 - 30 Nov' 25
Hi Folks! CAT is a prestigious exam for admission into pioneer institutes like the IIMs, and every MBA aspirant dreams of making it there regardless of their educational background. Careers360 brings you insights on how to crack the CAT QA section with just 30% coverage of the syllabus, especially if you are starting your preparation late. In this article, you will find an overview of the Quantitative Aptitude section of CAT 2025, details about the QA syllabus, the importance of QA scores in the overall percentile, tips on how to crack the section, and a clear CAT QA strategy. Stay tuned for more information!
This Story also Contains
- Introduction to CAT Quantitative Aptitude (QA)
- Understanding CAT QA Strategy
- 30% Syllabus Strategy for CAT Quantitative Aptitude
- Must-Do Topics for CAT Quantitative Aptitude
- Smart Preparation for CAT QA with Limited Time
- Time-Saving Techniques for CAT Quant Preparation
- Best resources & practice material for CAT Algebra
- CAT 2025 Preparation Resources by Careers360
Introduction to CAT Quantitative Aptitude (QA)
In CAT exam, quantitative aptitude section consists of 22 questions (14 MCQs and 8 TITA) to be solved in 40 minutes. Each wrong answer of MCQ will give you – 1 mark. For TITA type questions, there is no negative marking. Questions in this section generally range from easy to moderately difficult questions.
Importance of QA in the CAT Exam
MBA is a course for which having maths at +2 level is not mandatory. Students from arts background, biology background, or other background except mathematical background found this section difficult for them. If you have started preparation at right time, you will get plenty of time to cover maximum of syllabus with handsome amount of practice.
Why Focus on 30% of the Syllabus for CAT QA?
CAT exam syllabus of QA is very vast. If you start to prepare late for CAT, it is not possible to complete the whole syllabus in an effective manner. Let us have a look on the pattern of questions asked during last five years:
Year | Slot | Number System | Equations | Geometry | Time, Speed and distance | Others |
2020 | Slot 1 | 4 | 4 | 0 | 4 | 14 |
Slot 2 | 3 | 4 | 3 | 4 | 12 | |
Slot 3 | 5 | 2 | 3 | 3 | 13 | |
2021 | Slot 1 | 3 | 1 | 3 | 1 | 14 |
Slot 2 | 2 | 3 | 1 | 1 | 14 | |
Slot 3 | 2 | 1 | 3 | 1 | 15 | |
2022 | Slot 1 | 3 | 1 | 2 | 1 | 15 |
Slot 2 | 2 | 3 | 3 | 1 | 13 | |
Slot 3 | 4 | 3 | 3 | 3 | 9 | |
2023 | Slot 1 | 2 | 5 | 2 | 3 | 10 |
Slot 2 | 2 | 2 | 2 | 1 | 15 | |
Slot 3 | 4 | 2 | 3 | 1 | 12 | |
2024 | Slot 1 | 4 | 2 | 1 | 1 | 14 |
Slot 2 | 2 | 4 | 2 | 1 | 13 | |
Slot 3 | 3 | 4 | 3 | 1 | 11 |
As seen from above analysis, 30% coverage of syllabus covers almost 30 to 45% of weightage.
Understanding CAT QA Strategy
Are you struggling with QA section CAT?
Are you getting puzzled while opening a book to start your preparation of QA for CAT?
Here, Careers360 suggests some key strategies to start your preparation.
Key Components of a Successful CAT QA Strategy
The key components of a successful strategies for CAT QA involves:
Prepare a preparation schedule considering the small goals and ultimate goal.
Building Strong Fundamentals
Covering most of the syllabus
Learning speed maths and short tricks for quick solution
Give proper time to practice
Taking CAT Mock tests and analysing the performance
Focus on weaker areas
Time management
CAT 2025: VARC, DILR, and Quant MCQs & Weightages
Comprehensive CAT prep guide with focused practice on Verbal Ability, Data Interpretation & Logical Reasoning, and Quantitative Aptitude.
Download NowBalancing Speed and Accuracy for CAT Quantitative Aptitude
Speed or accuracy, what matters most?
Is it speed?
Or it is accuracy?
Confused?
Both matters equally.
Speed is important as we need to attempt as much as questions in the exam. In CAT QA section, you will have just 40 minutes to solve 22 questions. So, to maximize your score, you are required to attempt maximum number of questions. Attempting more questions make you relaxed for the other section as well and boost your confidence.
Let us assume that you have attempted 14 questions in CAT QA. Out of these 14 questions, 11 questions are MCQs and 3 questions are TITA. What if you have 6 questions incorrect (5 MCQs and 1 TITA), you overall score in QA will be $6 \times 3 – 5 \times 1 + 6 = 19$ which is very less as you were expecting. This is why accuracy is equally important.
Accuracy avoids negative marking, boost your overall percentile and gives you confidence.
Rushing to maximize your attempts is a major reason for a candidate to make mistakes in CAT QA. It states how crucial it is to maintain a steady pace. Take time to read the questions attentively and double-check what each question asks (without taking too much time), to boost accuracy and improve overall performance.
30% Syllabus Strategy for CAT Quantitative Aptitude
Syllabus of QA for CAT is very vast. But if you analyse the previous year pattern, the questions from topics like time and speed, time and work, percentage and its application, equations, number system, and geometry are frequently asked, covering 60% to 70% of test.
These topics form almost 40% to 50% of the syllabus. If you cover 30% of the syllabus, you can get a decent score in QA.
How to Identify the Most Important Topics for CAT QA
To know which topics are most important QA. You can refer to “Important topics for CAT”. Also, you should
Analyse at least previous 5 years question papers.
Make a list of topics which are frequently asked.
Watch interviews of candidates who got above 99% percentile in CAT.
Understand the pattern of the questions asked.
Take expert advice.
Maximizing Your Time: Focus on High-Weightage Topics
Are you worried about how to cover the complete syllabus within time?
No need to worry, you need to maximize your study time by following 30 -70 rule ie. 70% of your preparation time to be given on CAT high-weightage topics by identifying them as discussed above. 30% of your study time to be given on the topics which are having less weightage.
How this approach will benefit you?
It will boost your score
increases confidence
reduces stress.
How to create a custom study plan for CAT QA
To create a custom CAT study plan to prepare for QA, you can follow the given steps:
1. Assess your current knowledge by taking a mock test
2. Evaluate your areas of weakness
3. Make clear goal
4. Identify high weightage topics
5. Structure your study plans that includes the separate time for building fundamentals, practice sessions, and mock tests.
Must-Do Topics for CAT Quantitative Aptitude
Key topics in QA for CAT are:
Arithmetic: Percentage, Profit and Loss, Simple interest and compound interest, Time and Speed, Time and Work, Average and Mixture, Ratio and Partnership
Number System: HCF and LCM, divisibility rules, Factors, Trailing zeros
Algebra: Linear equations, quadratic equations, functions, polynomials, inequality, Logarithm, surds and Indices, Sequence and Series
Geometry and Mensuration: Triangles, Quadrilaterals, Circles, Polygons, Area and perimeter of 2 D figures, Area and Volume of 3 D figures, Coordinate Geometry
Modern Maths: Permutation and Combinations, Probability
Top 10 Important Topics for CAT QA
As per the previous year’s analysis, top 10 important topics and their key strategies for CAT Quantitative Aptitude are as follows:
1. Percentage and its application in profit and loss, SI and CI
Key Strategies:
(i). Learn the percentage to fractions conversion to solve the questions quickly.
For Ex: 33.33% of a number is calculated by dividing the number by 3. i.e. Fraction of 33.33% is 1/3.
(ii). Understand the key concepts of percentage change and successive change.
(iii). Solve Conceptually rather than using formulas.
(iv). Learn to apply the concept of percentages in the questions of profit and loss, SI and CI.
(v). Practice different kinds of problems.
2. Time, Speed, and Distance
Key Strategies:
(i). Divide questions in the categories of proportionality, Average Speed and Relative Speed.
(ii). Average Speed = $\frac {2 S_1S_2}{(S_1 + S_2)$
If distances covered with both speeds is same.
(iii). Use the concept of relative speed in solving the questions on Trains.
(iv). Conversion of speeds in appropriate should be done.
(v). Divide questions topic wise and practice different problems based on CAT Previous years questions.
3. Time and work
Key Strategies:
(i). Total work cab be taken as LCM of time taken by all the individuals.
(ii). Dividing questions concept wise may help in preparation.
(iii). Applying the concepts of time and work in the questions of Pipes and Cistern are solved by using the concept of time and work.
(iv). Use the concept of ratio to solve the questions on time and work.
4. Average and Mixtures
Key Strategies:
(i). At the initial stage of preparation, try to solve at-least 4 to 5 questions on averages and mixtures to check your understanding about the concept.
(ii). Learn the basic concept of average, weighted average, rule of allegation and concept of replacements.
(ii). Start with basic questions. (Probably level of difficulty 1)
(iv). After solving basic questions, learn some tricks and special cases to solve the problems quickly.
(v). Start to solve difficult problems from the books which are suggested in this article.
5. Equations and Inequality
Key Strategies:
(i). Use Elimination method by making coefficient of one variable equal in two equations.
(ii). Learn the rules for nature of solutions/roots.
(iii). Try to solve linear equations graphically.
(iv). In case of quadratic equations, check for feasibility of solutions.
(v). Learn important concepts of inequality such as
Modulus always opened in negative and positive value.
Learn the basic rules of solving inequality.
If -a > -b, then a < b.
If -a < -b, then a > b.
If a > b and c < 0 then ac < bc.
If a > b and c > d then a + c > b + d.
If the sides of an inequality are multiplied by the same negative quantity, the sign of inequality must be reversed.
6. Functions
Key Strategies:
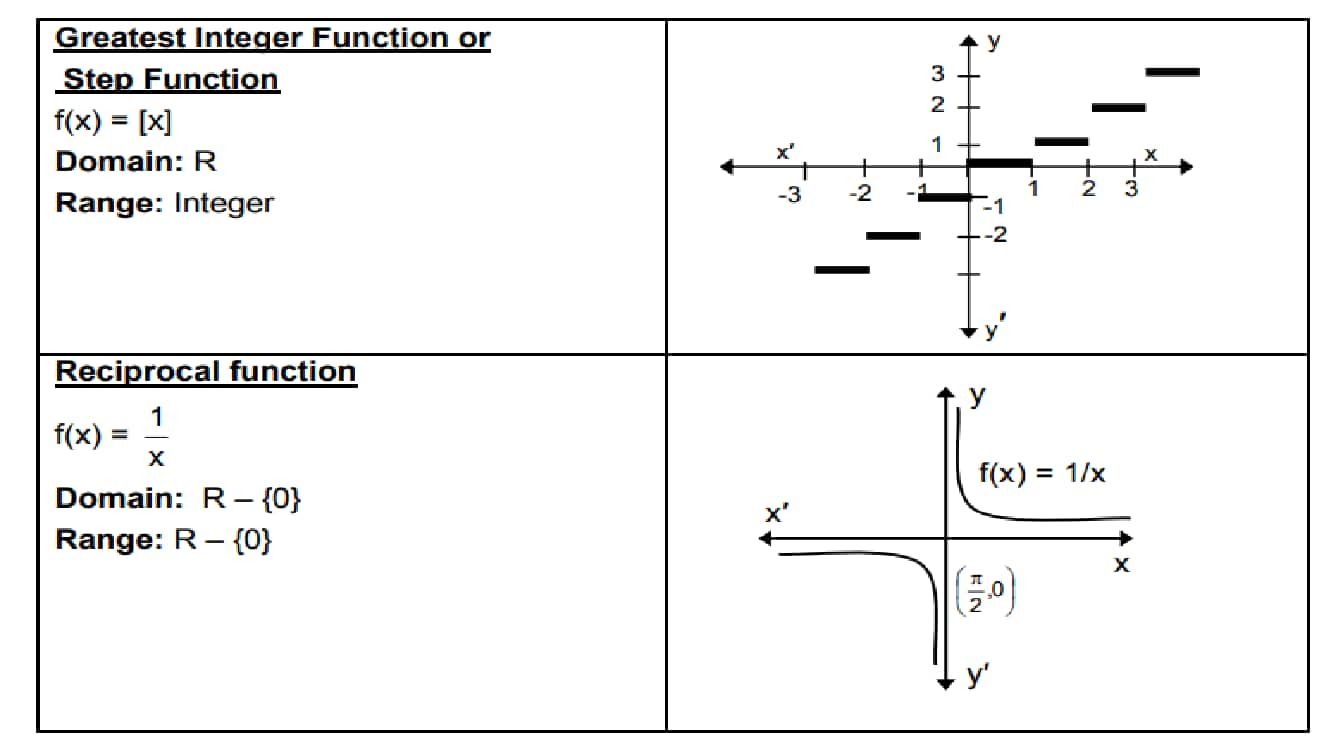
(i). Understand all types of functions and their related graphs to solve the questions based on functions effectively.
(ii). Learn the concept of composite Functions
It is function of some other function.
$ (g \circ f)(x) = g [f(x)] $
$ (f \circ g)(x) = f [g(x)] $
(iii). Understand the concept of Domain and Range:
Domain: Set of input values and represented on x-axis of the graph.
Range: Set of output values and represented on y-axis of the graph.
(iv) Practice questions of functions involving modulus function.
7. Logarithm
Key Strategies:
(i). Learn important properties of logarithm are as:
$\log_a (xy) = \log_a x + \log_a y$
$\log_a \left(\frac{x}{y}\right) = \log_a x - \log_a y$
$\log_a (x^n) = n \log_a x$
$\log_a \left( x^{m/n} \right) = \frac{m}{n} \log_a x$
$\log_a x = \frac{1}{\log_x a}$ (Base Change Operation)
$\log_a a = 1$
$\log_a 1 = 0$
$a^{\log_a x} = x$
(ii). Some common mistakes done by students while applying properties of logarithms which should be avoided:
$\log_a (x + y) \neq \log_a x + \log_a y$
$\log_a (xy) \neq (\log_a x)(\log_a y)$
(iii). Apply the concept of logarithm in questions where the number of digits is asked.
For example: find the number of digits in $2^{12}$
$\log 2^{12} = 12 \log 2 = 12 \times 0.3010 = 3.612$
Therefore, the number of digits in $2^{12}$ will be $(3 + 1) = 4$
8. Geometry and Mensuration
Key Strategies:
(i). Learn important properties of triangles such as Similarity, congruency, geometrical centres, sine rule, exterior angle property etc.
(ii). Learn to apply the formula of area of triangle in different scenarios.
(iii). Memorize Pythagoras triplets.
(iv). Learn important properties related to quadrilaterals and in what circumstances the properties are applied.
(v). Practice questions based on exterior and interior angle of regular polygons.
(vi). Practice questions on chords, tangents and secants, sectors and segments.
(vii). Understand difference between 2-D and 3-D figures.
(viii). Memorize all the formulas related to surface area and volume.
(ix). Use method of symmetry to solve the questions related to geometry and mensuration.
(x). Practice questions on coordinate geometry. Concept of symmetry plays an important role in solving the questions on coordinate geometry.
9. Sequence and Series
Key Strategies:
(i). Learn to apply the formula to find $n^{th}$ term and sum of $n$ terms.
(ii). Use some specific tricks such as
An AP of odd number of terms is to be assumed as
…, $a - 2d$, $a - d$, $a$, $a + d$, $a + 2d$, … [common difference $d$]
An AP of even number of terms is to be assumed as
…, $a - 3d$, $a - d$, $a + d$, $a + 3d$, … [common difference $2d$]
A GP of odd number of terms is to be assumed as
…, $\frac{a}{r}$, $a$, $ar$, … [common ratio $r$]
A GP of even number of terms is to be assumed as
…, $\frac{a}{r^3}$, $\frac{a}{r}$, $ar$, $ar^3$, … [common ratio $r^2$]
AM $\times$ HM = GM$^2$
AM $\geq$ GM $\geq$ HM
(iii). Practice Previous Years Questions to get an idea of questions.
10. Permutation and Combination
Key Strategies:
(i). Learn the concept of factorial.
(ii). Understand the conceptual clarity of permutations and combinations. You should be very clear about the uses of permutations and combinations in questions.
(iii). You can use following tricks and formulas
The number of permutations of $n$ distinct items taking $r$ items at a time is
$nP_r = \frac{n!}{(n-r)!}$$nP_n = n!$
$nC_r = nC_{n-r}$
Out of $n$ given things, the number of ways of selecting any number = $2^n - 1$.
Dividing $n$ items into two groups of $p$ and $q$ items = $\frac{n!}{q! , p!}$
If $p = q$ and two groups are not identical; the number of groups will be $\frac{n!}{{p!}^2}$
If $p = q$ and two groups are identical; number of groups will be $\frac{n! , 2!}{{p!}^2}$.
The number of diagonals in an $n$-sided regular polygon $= \binom{n}{2} - n$
(iv). Divide questions of distributions in following categories while solving:
Identical Objects Identical Places
Identical Objects Distinct Places
Distinct Objects Identical Places
Distinct Objects Distinct Places
(v). Solve questions conceptually rather than using formulas.
Why Trigonometry is essential for CAT QA
Although the direct questions from trigonometry are rarely asked, it is very crucial for CAT QA. It is essential because
You may find questions in geometry where the trigonometric ratios are required.
It is required in the questions of height and distance.
Trigonometric ratios are required in the questions of sector and segment, area using sine rule.
Trigonometric ratios are useful for quick calculations.
How to Approach These Topics
Developing Conceptual Strength: A strong knowledge of application of basic concepts to be developed.
Rigorous Practice on daily basis: Include practice sessions on QA in study plan on daily basis build speed and accuracy.
High-Weightage Topics first: As per the analysis of CAT previous years question papers focus on topics which constitutes highest weightage.
Smart Preparation for CAT QA with Limited Time
Sometimes students took time to decide whether they will appear for CAT or not, some students find difficulties especially in QA section. In this scenario, smart preparation is required. The following points may help you to boost your preparation:
List out the topics which are most important for CAT QA.
From these topics, which concepts are frequently asked.
Start with developing strong fundamentals.
Practice through Mock tests.
Solve previous years papers.
Using Mock Tests for Targeted Practice
Attempting Mock tests is an important tool to improve your QA score as it helps you to find
Where you stand
Are you in a right direction of your preparation
Your weak areas
How you should attempt your Mock?
Create an exam like environment at your home
Allot specific time to each question
Note down the time taken for each question
How to analyze the mistakes in quant?
Keeping a notebook to write down the mistakes will be helpful.
Write down topic, type of the question, related concept of the questions that are wrong.
Why the solution is wrong?
Why the right answer was right?
How to improve next time?
How to Use Previous Year Papers to Improve QA Scores
CAT previous years papers help you to get an idea of question type in CAT QA. By knowing this you can practice the questions on similar concepts.
You will be able to know the repeated concepts. Include the questions on those concepts in your practice. This practice will help you to achieve accuracy and speed in actual CAT exam.
You will find that on which area you should focus more.
Time-Saving Techniques for CAT Quant Preparation
For CAT QA, solving 22 questions in just 40 minutes is not an easy task. CAT QA is not easy section. But time management can be achieved by regular practice, learning mental maths, short tricks and taking practice tests
Fast Calculation Techniques for CAT QA
Learn to find the square, cube, square root, and cube roots using Vedic maths.
Use fractions to solve percentage etc mentally without using pen and paper.
Use Approximation and estimation.
Learn short tricks in each topic.
Solve through options.
Use unitary methods.
Solve by comparison.
Utilizing Mental Math for Quick Solutions in CAT Quant
What is mental maths?
Mental math is doing arithmetic calculations without using pen and paper.
You should do additions and subtraction up to 4-digit numbers mentally.
Multiply two-digit numbers without using pen.
Learns the tables, squares, and cubes up to 30.
Practice mental maths exercises regularly
Apply mental maths techniques in practice tests
Common Mistakes to Avoid While Preparing for CAT QA
1. Many students focus on learning the short tricks only without conceptual clarity. In relatively tough questions, short tricks do not work.
2. Not doing enough practice.
3. Students often do unplanned practice which leads them to leave some important concepts.
4. Just memorizing the things without conceptual clarity.
5. Not analysing CAT Mock tests to check their mistakes and identify their weaker areas.
6. Not focussing on time management.
7. Not considering previous years’ papers.
Best resources & practice material for CAT Algebra
1. Arun Sharma: A Quantitative Approach for CAT (7th Edition)
2. Quantitative Aptitude for CAT by Nishit K Sinha
CAT 2025 Preparation Resources by Careers360
The candidates can download the various CAT preparation resources designed by Careers360 using the links given below.
eBook Title | Download Links |
CAT 2025 Arithmetic Important Concepts and Practice Questions | |
CAT 2025 Algebra Important Concepts and Practice Questions | |
CAT 2025 Number System - Important Concepts & Practice Questions | |
CAT 2025 Exam's High Scoring Chapters and Topics | |
CAT Mock Test Series - 20 Sets, Questions with Solutions By Experts | |
Mastering CAT Exam: VARC, DILR, and Quant MCQs & Weightages | |
CAT 2025 Mastery: Chapter-wise MCQs for Success for VARC, DILR, Quant | |
CAT 2025 Quantitative Aptitude Questions with Answers | |
CAT 2025 Important Formulas | |
Past 10 years CAT Question Papers with Answers | |
CAT 2025 Quantitative Aptitude Study Material PDF - Geometry and Mensuration |
Frequently Asked Questions (FAQs)
Q: How many questions are asked in CAT QA?
A:
There will be 22 questions in QA section of CAT – 2025 to be solved in 40 minutes.
Q: How difficult is QA for CAT?
A:
The questions in CAT QA are ranging from easy to moderately difficult.
Q: What are the top 5 important topics for CAT QA?
A:
As per the previous years’ analysis
Time, speed, and distance
Equations
Average and Mixture
Geometry
Time and Work
Q: Do I need to be from a mathematics background to score well in QA ?
A:
No but if you are from mathematical background, you will have an upper edge. You can get good score in QA with consistent practice and mock tests.
Articles
Related Stories
|
Upcoming Bschool Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Popular Courses and Specializations
List of colleges accepting CAT
Browse Bschool Colleges by State
Questions related to CAT
On Question asked by student community
Have a question related to CAT ?
Hey! With a NEET score of 344 in the ST category, it is highly unlikely to get admission in any government BDS college in Delhi through the All India Quota. The cutoff for government BDS seats in Delhi usually falls around 400–450 for ST category, so your score is below that range.
You can consider private dental colleges, state quota seats in other states, or reattempt NEET next year to improve your chances.
Hello dear candidate,
YES, with NEET score 344in the ST category you have high chances of getting admission in a BDS College in J&K through JKBOPEE counselling.
check the seat availability and next participate in JKBOPEE Counselling with all the necessary documents.
Thank you.
Hey! With an All India Rank (AIR) of 302,821 in NEET and belonging to the BCE category, it is highly unlikely to get a BDS seat in Telangana under the state quota, as the closing ranks for BCE are usually below 50,000. You may consider applying to private colleges under management quota or explore BDS seats in other states, but the chances remain very limited with this rank.
At KIMS Amalapuram, the internship stipend for MBBS students is generally reported to be around 20,000 per month, though some students have mentioned that in certain years no stipend was provided at all, which means it can vary depending on the policies in place at the time of your internship. To get the most accurate and updated information, it is always best to confirm directly with the college administration or recent interns, but on average, you can expect a stipend in the range of 18,000-20,000 per month during the compulsory rotating internship.
Hello Aspirant,
Since your payment status shows "S" , it means your payment is successful. The "payment unsuccessful" message on the form is likely a temporary system error or a delay in updating.
Do not make another payment.
Making a second payment could cause a double debit, which is difficult to get a refund for. You should:
-
Wait 24-48 hours for the status to update automatically.
-
Download and save a copy of your form and a screenshot of the "S" payment status as proof.
-
Check your bank statement to confirm the money has been debited.
-
If the issue is not fixed after 48 hours, contact the official CAT helpdesk immediately with your transaction details.
Popular CAT Questions
Directions for question :
M/s Deloitte Touche Tohmatsu Limited, one of the top four audit and accounting firms in the world with headquarters at London, UK, and with an operational presence in 153 countries, hires Management Trainees (MT) from all the premier management institutes of India thrice every year, in the months of January, May and September.
Each new group of Management Trainees (MT) have to go through a four month rigorous training schedule, after which they have to pass through a test consisting of a written assessment and a case-analysis. The top hundred ranked Management Trainees (MT) based on the performance in the test are confirmed as Management Executives (ME). The rest are given the opportunity of undergoing the training for four months one more time along with the next batch of Management Trainees (MT) and then passing through the subsequent test consisting of the written assessment and case-analysis. The Management Trainee (MT) who fails to get confirmed as a Management Executive (ME) the second time is fired.
The scatter-graph below depicts the number of Management Trainees (MT) at Deloitte taking the tests from January 2020 till May 2022, and the vis-à-vis hired Management Trainees (MT) at Deloitte who were fired :
It is also known that for the month of September 2019 at Deloitte, 96 hired Management Trainees (MT) failed to be confirmed as a Management Executive (ME) the first time, and that 36 hired Management Trainees (MT) were fired.
Question :
In which test did the minimum number of Management Trainees (MT) get confirmed as a Management Executive (ME) in the second attempt ?
Option: 1
September 2020
Option: 2
May 2021
Option: 3
January 2021
Option: 4
January 2022
Directions for question:
The bar-graph given below shows the foreign exchange reserves of Nepal (in million Rupees) from 2014 to 2021. Answer the following questions based on the graph :
Question:
What was the percentage increase (rounded to the nearest integer, if deemed necessary) in the foreign exchange reserves in 2020 over 2016 ?
Option: 1 None
Option: 2 None
Option: 3 None
Option: 4 None
MBA/PGDM Admissions OPEN
Great Lakes Institute of Management PGPM Admissions 2026
ApplyAdmissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
IMT Ghaziabad PGDM Admissions 2026
ApplyAACSB, NBA & SAQS Accredited | H-CTC 41.55 LPA | Merit Based Scholarship
IBSAT 2025-ICFAI Business School MBA/PGPM 2026
ApplyIBSAT 2025-Your gateway to MBA/PGPM @ IBS Hyderabad and 8 other IBS campuses | Scholarships worth 10 CR
FLAME University | MBA 2026
ApplyNAAC A++ Grade | MBA program graded A** (National) by CRISIL | AACSB, ACBSP and BGA Member
Atlas SkillTech University MBA Admissions 2026
ApplyIndia’s first Urban Multidisciplinary University | Case-based pedagogy | Industry-endorsed curriculum
K J Somaiya Institute of Management MBA Admissions 2026
ApplyHighest Package 27.25 LPA | Top 100 Average package 16.65 LPA | AACSB Accredited | Ranked 52 by QS International
CAT Notifications
Never miss an CAT update
Get timely CAT updates directly to your inbox. Stay informed!