CAT 2026 Geometry: Study These 5 Theorems and Solve Most Questions Easily

Why Geometry Matters in CAT Quant?

Geometry is very important for CAT in certain ways:

• Geometry constitutes a healthy weightage in CAT exam.

• Geometry is interconnected with the other topics such as Mensuration, Geometry, and Coordinate geometry.

• Geometry questions require conceptual clarity rather than mathematical calculations.

• It creates a foundation for other topics as well.

Number of Geometry Questions and Difficulty Level Analysis in CAT (2025–2020 Trend)

Key Takeaways

1. Geometry has appeared consistently in CAT since 2021, with most slots featuring 2–3 questions.

2. CAT 2025 continued the trend with 3 geometry questions in all three slots.

3. Most geometry questions fall in the easy to moderate category.

4. Hard geometry questions are relatively rare, usually limited to 0–1 question per slot.

5. CAT 2020 was an exception, with Geometry appearing only in Slot 2.

Most asked Geometry questions, CAT candidates face

Important Geometry Theorems for CAT 2026 - Just 5 You Need

Since Geometry is very vast topic in CAT Quantitative Aptitude, it contains several theorems and concepts to understand. You will find important theorems for CAT Geometry preparation in this article. You should have knowledge of basic concepts like

• Relation between angles between two parallel lines

• Angle sum properties

• Exterior angle sum property

• Similarity and Congruency of triangles

• Properties related to quadrilaterals and Polygons

• Properties of Circles, Sector, and Segment.

In this section, we are going to discuss 5 important theorems that covers almost 80% of CAT questions from geometry.

Why only 5 theorems cover 80% questions

The five theorems that we are going to discuss in this article covers almost 80% of the CAT geometry questions since these theorems are most versatile.

For example: Pythagoras theorem is important for the questions related to triangle, trigonometry, quadrilateral, and circles.

Theorem 1 - Pythagoras and Its Variations

The Pythagorean theorem states that in a right-angled triangle; the square of the longest side is equal to the sum of the squares of the other two sides.

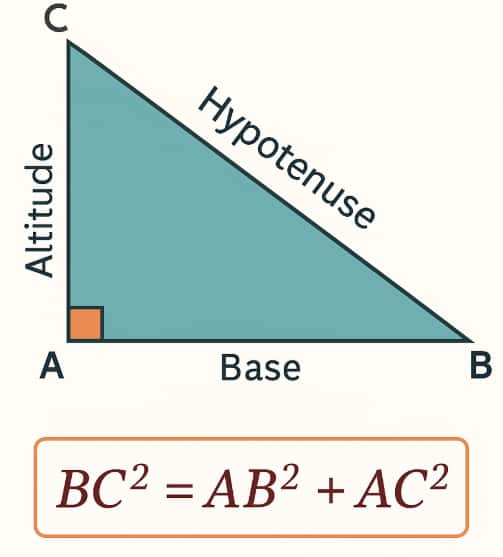
The longest side in a right-angled triangle is known as Hypotenuse.

Also, if in a triangle, $a^2 + b^2 > c^2$, where '$c$' is the longest side of the triangle, the triangle is obtuse angled triangle.
if in a triangle, $a^2 + b^2 < c^2$, where '$c$' is the longest side of the triangle, the triangle is acute angled triangle.

Direct applications in right triangles

Pythagoras theorem is directly used in a right-angled triangle:

• To find the third side if two sides are given.

• To check whether the given triangle is right angled triangle or not.

• If one of the acute angles is given and we need to relate all the sides of an equilateral triangle.

For Example:
In a triangle ABC, right angles at A, angle B is 30o, determine the ratio of all the sides.
Solution:
For angle B, Base is AB and Perpendicular is AC.
So, $\sin 30^\circ = \frac {AC}{AB}$
⇒ $\frac 12 = \frac {AC}{AB}$
Let $AB = 2, AC = 1$, then $BC^2 = AC^2 + AB^2$
So, $AC = \sqrt {2^2 - 1^1} = \sqrt 3$

Common CAT question types using Pythagoras and PYQ

In CAT, the questions on Pythagoras theorem, are asked on

• The application of Pythagoras theorem in right angled triangle to find the unknown side

• The application of Pythagoras theorem in quadrilateral and circles

Q.1) In a right-angled triangle ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ΔABP, ΔABQ and ΔABC are in arithmetic progression. If the area of ΔABC is 1.5 times the area of ΔABP, the length of PQ, in cm, is:

A) 2

B) 3

C) 4

D) 8

Solution:-
Area of ∆ABC = $\frac{1}{2} \times 5 \times 12$ = 30 sq cm
So, Area of ∆ABP = $\frac {30}{1.5}$ = 20 sq cm
And, Area of ∆ABQ = $\frac {30 +20}{2}$ = 25 sq cm (Since the areas are in AP)
Now, Area of ∆ABP = $\frac{1}{2} \times 5 \times BP$ = 20 sq cm
⇒ $BP = 8$ cm
Now, Area of ∆ABQ = $\frac{1}{2} \times 5 \times BQ$ = 25 sq cm
⇒ $BQ = 10$ cm
So, PQ = $BQ-BP = 10 -8=2$ cm
Hence, the correct answer is option (1).

Q.2) In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP: PQ: QC is

A) 1:1:2

B) 1:2:4

C) 2:4:1

D) 2:4:3

Solution:-

The areas of the figures $ABP$, $APQ$, and $AQCD$ are in geometric progression.

Area of $ABP = m$.

Area of $APQ = mr$.

Area of $AQCD = mr^2$.

Also, Area of $AQCD = 4 \times$ (Area of $ABP$),

$\Rightarrow mr^2 = 4m$,

$\Rightarrow r = 2$.

So, the total area = Area of rectangle = $9 \times 6 = 54$.

So, $m + 2m + 4m = 54$,

$\Rightarrow m = \frac{54}{7}$.

Area of $ABP = m = \frac{54}{7}$,

$\Rightarrow \frac{1}{2} \times AB \times BP = \frac{54}{7}$.

$\Rightarrow BP = \frac{12}{7}$ (since $AB = 9$).

Area of $ABQ = 2m + m = \frac{162}{7}$,

$\Rightarrow \frac{1}{2} \times AB \times BQ = \frac{162}{7}$.

⇒ BQ = $\frac{36}{7}$ (Since AB = 9)

Now, PQ = BQ - BP =$\frac{36}{7}$ - $\frac{12}{7}$ = $\frac{24}{7}$
QC = BC - BQ = 6 - $\frac{36}{7}$ = $\frac{6}{7}$

Now, BP: PQ: QC = ($\frac{12}{7}$) : ($\frac{24}{7}$) : ($\frac{6}{7}$) = 2:4:1

Hence, the correct answer is option (3).

Shortcut methods to save time

To solve the questions based on Pythagoras theorem quickly

• Learn squares up to 30.

• Learn Pythagorean triplets (Pythagorean triplets contain three numbers satisfying the Pythagoras theorem)

Theorem 2 - Similar Triangles

Triangles having exact similar shape but different sizes are similar triangles.

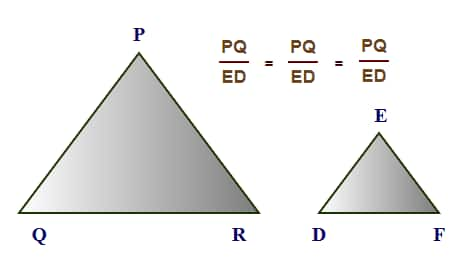
Two triangles are said to be similar if either their corresponding angles are equal or corresponding sides are in equal proportion.

Key properties to remember

Also,
If triangle ABC is similar to triangle PQR, then
$(\frac {AB}{PQ})^2 = (\frac {BC}{QR})^2 = (\frac {AC}{PR})^2 =\frac {ar(ABC)}{ar(PQR)} $
and $(\frac {AB}{PQ}) = (\frac {BC}{QR}) = (\frac {AC}{PR}) =\frac {ar(ABC)}{ar(PQR)} $

Application in height-distance

Application of similar triangles in the questions of height and distance can be understood with the help of following example:

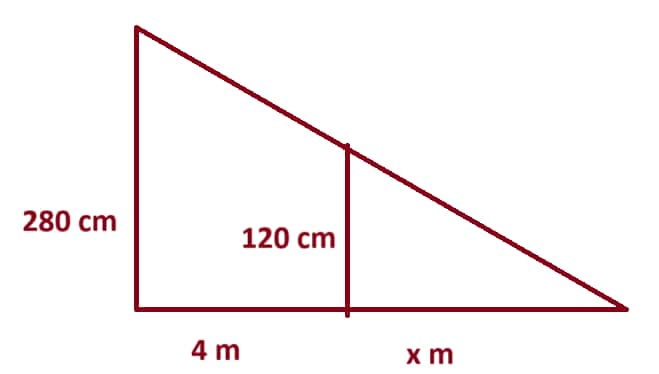
A boy of height 120 cm is walking away from the base of a tower at a speed at 0.8 m/sec. If the tower is 2.8 m above the ground, find the length of the shadow of boy after 5 seconds.

From the information given in the question
The larger triangle and smaller triangle are similar as one angle of each is of 90 degrees and the other is common.

So, $\frac {280}{120} = \frac {4+x}{x}$
So, $x = 3$ metres

Theorem 3 - Basic Proportionality Theorem (Thales Theorem)

The Basic Proportionality Theorem (Thales’ theorem), states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.

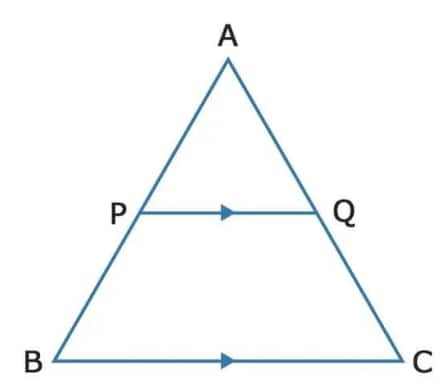
If PQ || BC, then $\frac {AP}{PB} = \frac {AQ}{QC}$

Some Important results derive from BPT:

1. $\frac {AP}{AB} = \frac {AQ}{AC}$
2. If P and Q are mid points of AB and AC respectively, then PQ = ½ BC.

How CAT frames tricky questions using BPT

In CAT, direct questions from BPT are rarely asked. They integrate BPT with the other topics like

• Complex diagram of quadrilateral in which BPT will be used to relate the sides of triangles formed inside the quadrilateral to find the unknowns.

• In cyclic quadrilaterals in which diagonals are intersecting.

• In circles to relate chords, radius, and tangents.

• In coordinate geometry where equation of two or more intersecting lines are given in a plane and we have to determine the coordinates of intersecting points or lengths of sides forming triangles to find the area etc.

Theorem 4 - Circle Geometry (Tangent & Secant Properties)

Tangent is a line that touches a circle at one point only while a secant intersects a circle at two points.

Tangent-radius relation (most tested)

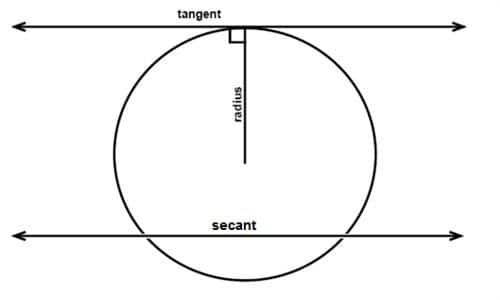
Radius is perpendicular to the tangent at point of contact. Questions based on tangent and radius relations are frequently asked. An important relation is given below:

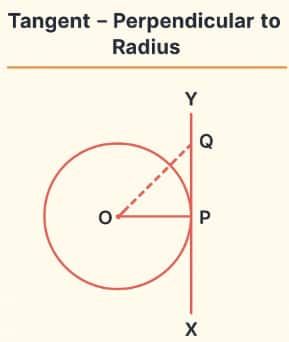
$OP$ is perpendicular to $PQ$.
So, $OQ^2 = OP^2 + PQ^2$

Radius - chord relation

Perpendicular to the chord from the centre of a circle bisects the chord. An important relation is given below:

Power of a point theorem in CAT questions

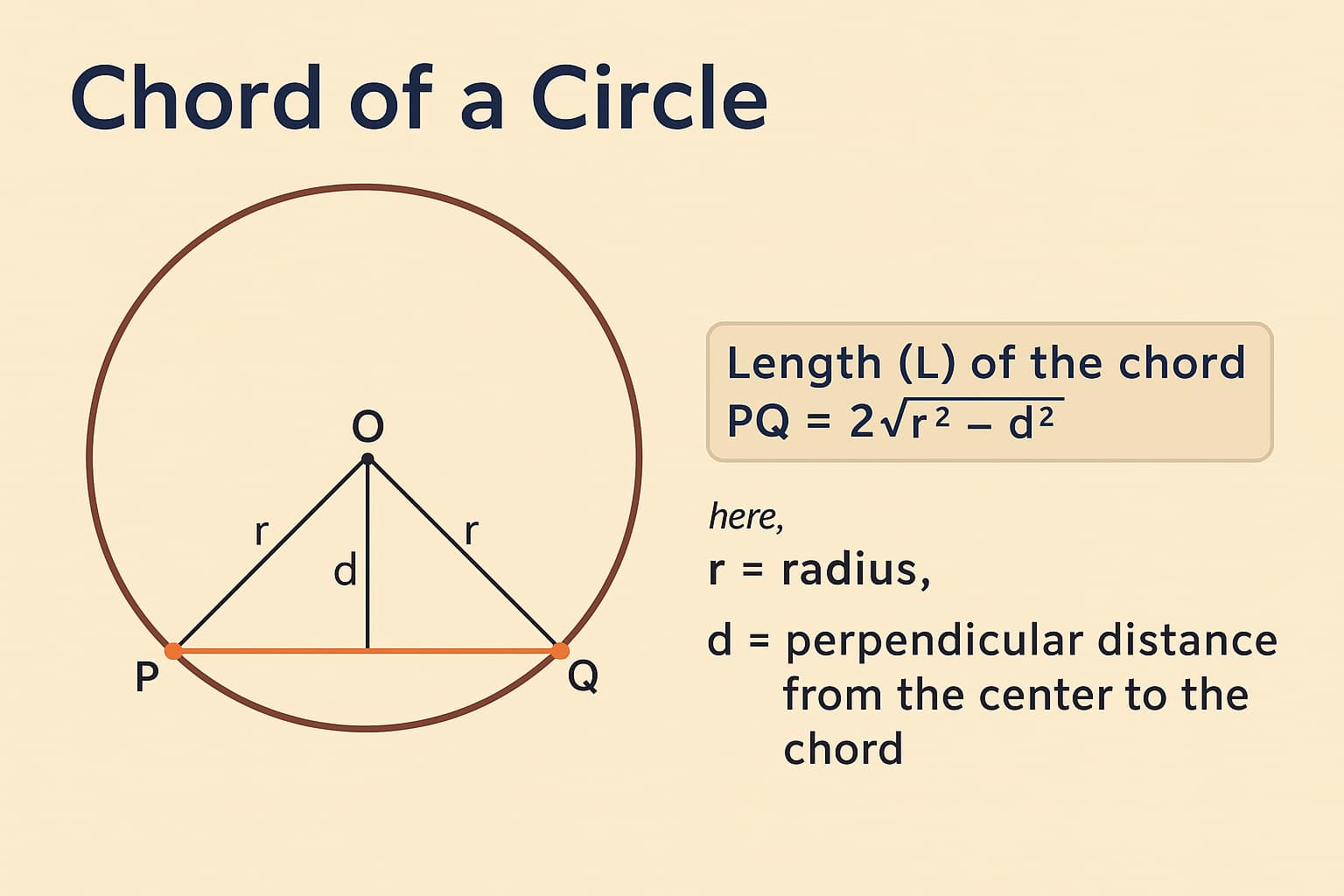
Point theorem is applied to find the length of a line segment, chord, and tangent in CAT questions.

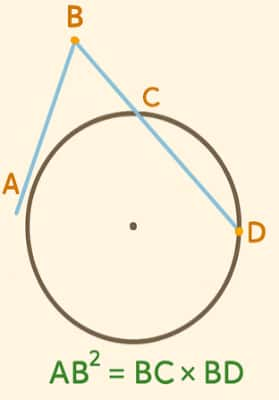
A point outside the circle:
A tangent drawn from point B outside the circle at point A, and a secant from B intersects the circle at C and D. Then $AB^2 = BC \times BD$.

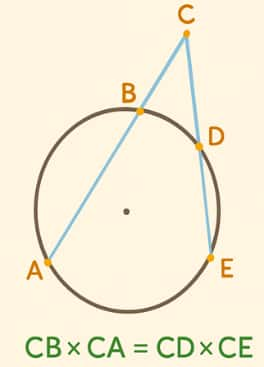
Two secants drawn from a point outside the circle:

Two secants from point C intersect the circle at A, B and D, E respectively. Then CA × CB = CD × CE.

Two intersecting chords inside the circle:

Two chords AB and CD intersecting at a point P inside a circle, then PA × PB = PC × PD.

Tangent - Secant theorem:
A tangent drawn from point P outside the circle at point C, and a secant from P intersects the circle at B and A. Then $PC^2 = PA \times PB$.

Theorem 5 - Area Theorems (Heron’s Formula & Median Theorem)

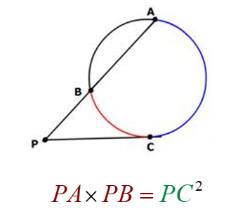
There are several formulas to find the area of a triangle but Herons formula can be used for any triangle.

If the sides of a triangle are a, b, and c, then the area of a triangle is given by
$\text {Area of a triangle} = \sqrt {s(s-a)(s-b)(s-c)}$
where s is semi perimeter of the triangle given by
$s=\frac {a+b+c}{2}$

Median is a line joining a vertex of triangle to the mid-point of the opposite side. The intersection point of all medians is known as Centroid. Centroid divides a median in the ratio 2 : 1 from vertex to the side.

Fast calculation of triangle areas and some important results:

There are some concepts and formulas used to determine the area of a triangle effectively.

1. For scalene triangle (three sides are known):

Use Herons formula (Discussed above)

2. For an equilateral triangle (Side is known)

Area = $\frac {\sqrt 3}{4} a^2$, where $a$ is the side of the triangle.

3. Two sides and angle between them is known

Area = $\frac{1}{2}$ × product of two sides × sine of the included angle

4. If inradius ($r$) and semi perimeter (s) is known

Area = rs

5. If circumradius ($R$) and three sides are known

Area = $\frac{abc}{4R}$, where R = circumradius

6. Universal formula to determine the area of a triangle

Area = $\frac{1}{2}$ × base × height

Application in quadrilaterals and polygons

Herons’ formula can be used to find the area of a quadrilateral and polygon. To find the area of a quadrilateral and polygon, divide it in to triangles and apply the Herons formula to each triangle.

Example: Dimensions of quadrilateral are as shown in the figure. Find the area.

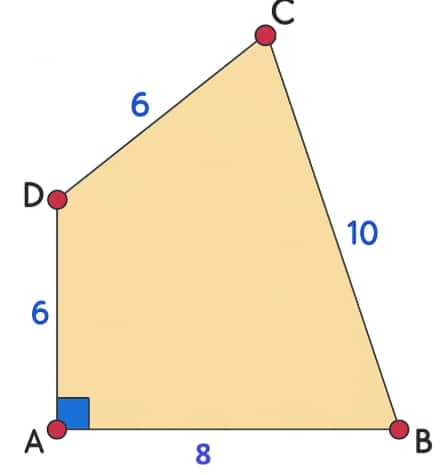
Using Pythagoras theorem, ${BD}^2 = 6^2 + 8^2$ ⇒ BD = 10

Area of ABCD = Area of ΔABD + Area of ΔBCD

Area of ΔABD = $\frac 12 \times 6 \times 8$ = 24 sq units

Find area of triangle BCD using Heron’s formula
s = (6 + 10 + 10)/2 = 13
Area of ΔBCD = $\sqrt {13(13-6)(13-10)(13-10)}$
$= 3 \sqrt {91}$ sq units

So, Area of ABCD = 24 + 3 $\sqrt {91}$ sq units

Similarly, we can determine the area of a polygon.

Solved Past 5 Years’ Questions with Solutions of Geometry for CAT

Q.1) From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is:

A) $\mathrm{\frac{\sqrt{3} s^2}{2}}$

B) $\mathrm{{\frac{2 s^2}{\sqrt{3}}} }$

C) $\mathrm{\frac{s^2}{2 \sqrt{4}} }$

D) $\mathrm{\frac{s^2}{2 \sqrt{3}} }$

Solution:-

Based on the question: A D, C E and B F are the three altitudes of the triangle. It has been stated that
$\mathrm{ \{\mathrm{GD}+\mathrm{GE}+\mathrm{GF}=\mathrm{s}\} }$
Now since the triangle is equilateral, let the length of each side be "a".
So the area of the triangle will be
$\mathrm{ \frac{1}{2} \times G D \times a+\frac{1}{2} \times G E \times a+\frac{1}{2} \times G F \times a=\frac{\sqrt{3}}{4} a^2 }$
Now, $\mathrm{ G D+G E+G F=\frac{\sqrt{3} a}{2} \text { or } s=\frac{\sqrt{3} a}{2} \text { or } a=\frac{2 s}{\sqrt{3}} }$
Given the area of the equilateral triangle $\mathrm{ =\frac{\sqrt{3}}{4} a^2 }$
substituting the value of 'a' from above, we get the area { in terms 's'} $\mathrm{ =\frac{s^2}{\sqrt{3}}}$
Hence, the correct answer is option (4).

Q.2) Let C1 and C2 be concentric circles such that the diameter of C1 is 2 cm longer than that of C2. If a chord of C1 has length 6 cm and is tangent to C2, then the diameter, in cm, of C1 is:

A) 10

B) 8

C) 12

D) 16

Solution:-

Now we know that the perpendicular from the centre to a chord bisects the chord. Hence at the point of intersection of tangent, the chord will be divided into two parts of 3 cm each. As you can clearly see in the diagram, a right-angled triangle is formed there.
So, $\mathrm{(r+1)^2=r^2+9 \text { or } r^2+1+2 r=r^2+9 \text { or } 2 r=8 \text { or } r=4 \mathrm{~cm}}$
Therefore, the radius of the larger circle is 5 cm and the diameter is 10 cm.
Hence, the correct answer is option (1).

Q.3) Suppose the length of each side of a regular hexagon ABCDEF is 2 cm. If T is the midpoint of CD, then the length of AT, in cm, is:

A) $\sqrt{13}$

B) $\sqrt{14}$

C) $\sqrt{12}$

D) $\sqrt{15}$

Solution:-

Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangles forming the hexagon.
Hence, its length should be twice the side of the hexagon, in this case, 4 cm.

Now, AD divided the hexagon into two symmetrical halves.
Hence, AD bisects angle D, and hence, $\angle$ADC is 60°.
We can find out the value of AT using the cosine formula:

$\begin{aligned} & \mathrm{AT}^2=4^2+1^2-2 \times 1 \times 4 \cos 60° \\ & ⇒\mathrm{AT}^2=17-4=13 \\ & \therefore A T=\sqrt{13}\end{aligned}$

Hence, the correct answer is option (1).

Q.4) A circle of diameter 8 inches is inscribed in a triangle ABC, where $\angle A B C=90^{\circ}$. If BC = 10 inches, then the area of the triangle in square inches is:

A) 120

B) 100

C) 80

D) 90

Solution:-
Diameter = 8 inches; So, radius = 4 inches
Let p be the perpendicular and h be the hypotenuse of the triangle.
We know that inradius = $\frac{(\text { Perpendicular }+ \text { Base }- \text { Hypotenuse })}{2}$
$
⇒4=\frac{(p+10-h)}{2}
$
$
⇒\mathrm{h}-\mathrm{p}=2$
$ ⇒\mathrm{h}=\mathrm{p}+2
$
Now, $\mathrm{P}^2+100=\mathrm{h}^2$
$
\begin{aligned}
&⇒ p^2+100=(p+2)^2 \\
& ⇒p^2+100=p^2+4 p+4 \\
&⇒ 4 p=96 \\
& \therefore p=24
\end{aligned}
$
Hence, area of the $\triangle$ABC $=\frac{1}{2} \times 10 \times 24=120$

Hence, the correct answer is option (1).

Q.5) All the vertices of a rectangle lie on a circle of radius $r$. If the perimeter of the rectangle is P, then the area of the rectangle is:

A) $\frac{P^2}{16}-r^2$

B) $\frac{P^2}{8}-2 r^2$

C) $\frac{P^2}{2}-2 P r$

D) $\frac{P^2}{4}-2 P r$

Solution:-
Let the length and breadth of the rectangle be $l$ and $b$, respectively.
So, the area of the rectangle = $lb$
$\begin{aligned} &\text{Now, } l^2+b^2=4 r^2 \\ &\text{Also, } \mathrm{P}=2(l+b) \\ &⇒ \frac{P}{2}=l+b\end{aligned}$
Squaring on both sides, we get
$\begin{aligned} & \frac{P^2}{4}=l^2+b^2+2 l b \\ & ⇒\frac{P^2}{4}=4 r^2+2 l b \\ &⇒ \frac{P^2}{8}-2 r^2=l b\end{aligned}$
So, the area of the rectangle is $\frac{P^2}{8}-2 r^2$.
Hence, the correct answer is option (2).

Q.6) Suppose the medians BD and CE of a triangle ABC intersect at a point O. If the area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is:

A) 9

B) 12

C) 15

D) 18

Solution:-

Given: The medians BD and CE of a triangle ABC intersect at a point O and the area of triangle ABC is 108 sq. cm.
(Area of ABD):(Area of BDC) $=1: 1$
Therefore, the area of $A B D=54$
Area of $A D E$ : Area of $E D B=1: 1$
Therefore, the area of $A D E=27$
$\mathrm{O}$ is the centroid and it divides the medians in the ratio of 2:1
So, (Area of BEO):(Area of EOD) $=2: 1$
⇒ Area of EOD $=9$
Hence, the correct answer is option (1).

Q.7) $A B C D$ is a rectangle with sides $A B=56 \mathrm{~cm}$ and $B C=45 \mathrm{~cm}$, and $E$ is the midpoint of side $C D$. Then, the length, in cm , of radius of incircle of $\triangle A D E$ is

Solution:-

Given: $AB = 56$ cm, $BC = 45$ cm, so $AD = 45$ cm, $CD = 56$ cm.
$E$ is the midpoint of $CD \Rightarrow CE = 28$ cm.

In triangle $ADE$, use Pythagoras theorem:
$DE^2 = AD^2 + CE^2$
$⇒DE^2 = 45^2 + 28^2 = 2026 + 784 = 2809$
$⇒DE = \sqrt{2809} = 53$ cm

Using inradius formula for triangle with sides $a$, $b$, $c$:
$r = \frac{a + b - c}{2}$, where $c$ is the longest side

Here, $a = 45$, $b = 28$, $c = 53$
So, $r = \frac{45 + 28 - 53}{2} = \frac{20}{2} = 10$ cm

Hence, the correct answer is $10 \text{ cm}$.

Q.8) A quadrilateral ABCD is inscribed in a circle such that AB: CD = 2:1 and BC: AD = 5:4. If AC and BD intersect at the point E, then AE: CE equals:

A) 1:2

B) 5:8

C) 8:5

D) 8:7

Solution:-
In $\triangle AED$ and $\triangle BEC$
$\angle A D E=\angle B C E$ (Angles made by same are on the same side of the triangles are equal)
$\angle A E D=\angle B E C$ (Vertically opposite angles are equal)
$\triangle A D E \sim \triangle B C E$ (By AA similarity criteria)
So, $\frac{A D}{B C}=\frac{D E}{C E}$.............(1)
In $\triangle C E D$ and $\triangle BEA$
$\angle E D C=\angle B A E$ (Angles made by same are on the same side of the triangles are equal)
$\angle C E D=\angle B E A$ (Vertically opposite angles are equal)
$\triangle C D E \sim \triangle B A E$ (By AA similarity criteria)
So, $\frac{C D}{A B}=\frac{D E}{A E}$..................(2)
From (1) and (2), we get, $\left(\frac{A D}{B C}\right)\left(\frac{A B}{C D}\right)=\left(\frac{D E}{C E}\right)\left(\frac{A E}{C E}\right)$
So, $\left(\frac{A E}{C E}\right)=\left(\frac{4}{5}\right)\left(\frac{2}{1}\right)=\frac{8}{5}$
Hence, the correct answer is option (3).

CAT 2026 Geometry Shortcuts & Smart Approaches

To solve the questions on Geometry effectively, use diagrams to interpret the question, eliminate inappropriate options, learn formulas, understand the questions properly.

Elimination technique in MCQs

In MCQs, try to eliminate wrong options by using

• Ratios

• Using angle sum property in the questions where an unknown angle needs to determine.

• Using the constraints given in the question.

Approximations and diagrams for speed
In the questions related to geometry, drawing diagrams is one of the key aspects.

• To increase speed, draw an approximate and rough diagram that should make you understand the problem.

• Label the key points, angles, and measurement in the diagram.

Geometry formulas for CAT exam to memorize

• There are hundreds of formulas in Geometry. You need to memorize the key formulas of the concepts that are frequently asked in CAT quantitative aptitude.

• There are some questions that can be solved using concepts easily. For such questions, avoid the formulas.

• In the next section, we are going to summarize the key formulas.

Geometry Formulas for CAT 2026 Exam - The Ultimate Revision List

Common Mistakes in CAT 2026 Geometry Preparation

CAT 2026 Geometry Preparation Strategy - Step by Step

We divide our strategy to prepare Geometry for CAT in 3 steps:

Step 1: Work on to build fundamentals:
First, understand the concepts related to angles between two parallel lines and intersecting lines such as corresponding angles, alternate interior angles, vertically opposite angles etc. Also, learn complementary angles and supplementary angles.

Understand theorems related to triangles, quadrilaterals, and Circles.

Step 2: Gain mastery in formulas and drawing diagrams:
Prepare a list of all formulas and practice questions using diagrams. This will help you in saving time and increase accuracy.

Step 3: Taking Mock tests and analyse them:
Include practice tests and CAT Mock tests in your preparation to identify your weak areas to improve. Also make a log to note down the mistakes you are making regularly. Work on the mistakes to rectify. Also, monitor your score after each test and give a direction to your preparation accordingly.

Best books for CAT 2026 Geometry

Geometry questions in CAT often test conceptual understanding rather than direct formula application, making it important to study from the right resources. The books listed below can help you build strong fundamentals, learn problem-solving techniques, and practice CAT-level Geometry questions effectively.

CAT 2026 Preparation Resources by Careers360

Candidates can download the various CAT preparation resources designed by Careers360 using the links given below.