कैट प्रश्न पत्र 2024 जारी (CAT question paper 2024 in hindi) - समाधान सहित पेपर डाउनलोड करें

कैट प्रश्न पत्र 2024 (CAT Question Papers 2024 in Hindi) : देश के प्रतिष्ठित प्रबंधन संस्थानों में एमबीए प्रवेश के लिए 170 शहरों में 24 नवंबर 2024 को कैट 2024 परीक्षा का सफलतापूर्वक आयोजन किया गया। कैट 2024 प्रश्न पत्र पीडीएफ मुफ्त डाउनलोड यहां उपलब्ध है। कैट 2024 परीक्षा में शामिल होने वाले छात्र आज इस पेज के माध्यम से कैट 2024 स्लॉट 1 प्रश्न पत्र, कैट स्लॉट 2 पेपर और कैट स्लॉट 3 प्रश्न पत्र डाउनलोड कर सकते हैं। कैट 2024 के प्रश्न पत्र का पैटर्न स्लॉट 1 के लिए थोड़ा बदला है, जैसा कि छात्रों ने बताया- 66 की जगह कुल 68 प्रश्न पूछे गए। DILR सेक्शन में 22 प्रश्न हैं।
कैट स्कोर स्वीकार करने वाले कम फीस वाले शीर्ष कॉलेज

कैट 2024 में उपस्थित होने वाले उम्मीदवारों को कैट मॉक टेस्ट (CAT mock test in hindi) के साथ कैट प्रश्न पत्र हल करना चाहिए। पिछले वर्ष के कैट प्रश्नपत्रों को हल करने के कई फायदे हैं, जैसे पूछे गए प्रश्नों के प्रकार, अंकन योजना, विभिन्न अनुभागों द्वारा दिए जाने वाले वेटेज को समझना और, सबसे महत्वपूर्ण बात यह है कि किसी समस्या को तुरंत हल करना सीखना, जो कैट में मदद करेगा। इस लेख के माध्यम से वर्षवार कैट प्रश्न पत्र पीडीएफ डाउनलोड कर सकते हैं। कैट प्रश्न पत्र का अध्ययन का कैट की तैयारी कर रहे उम्मीदवारों के लिए सबसे अच्छा स्रोत है तथा प्रभावी तैयारी में भी मदद करता है।
कैट परीक्षा विश्लेषण | सर्वश्रेष्ठ प्लेसमेंट वाले कैट कॉलेज | कैट अनौपचारिक आंसर की 2024

कैट 2024 प्रश्न पत्र पीडीएफ मुफ्त डाउनलोड करें (CAT 2024 Question Paper PDF Download Free)

नीचे दी गई तालिका से कैट 2024 प्रश्न पत्र स्लॉट-वार फ्री डाउनलोड करें।

कैट 2024 आंसर की और रिस्पांस शीट (CAT 2024 Answer Key and Response Sheet)

आईआईएम कलकत्ता ने आधिकारिक तौर पर अपनी आधिकारिक वेबसाइट पर स्लॉट 1, 2 और 3 के लिए कैट 2024 उत्तर कुंजी और प्रतिक्रिया पत्रक जारी कर दिया है।

कैट 2024 स्लॉट 1 उत्तर कुंजी

कैट 2024 स्लॉट 2 उत्तर कुंजी

कैट 2024 स्लॉट 3 उत्तर कुंजी

कैट 2024 प्रश्न पत्र परसेंटाइल के प्रारंभिक अनुमान (कुल मिलाकर)

कैट 2024 स्लॉट 3 प्रश्न (मेमोरी आधारित)

Q 1. $3^a=4,4^b=5,5^c=6,6^d=7,7^e=8,8^f=9$. abcdef $\Rightarrow ?$

Solution:

From $3^a=4$, take log:

$a=\log _3 4$

From $4^b=5$ :

$b=\log _4 5$

From $5^c=6$ :

$c=\log _5 6$

From $6^d=7$ :

$d=\log _6 7$

From $7^e=8$ :

$e=\log _7 8$

From $8^f=9$ :

$f=\log _8 9$

$a b c d e f=\left(\log _3 4\right)\left(\log _4 5\right)\left(\log _5 6\right)\left(\log _6 7\right)\left(\log _7 8\right)\left(\log _8 9\right)$

Using the change of base formula $\log _a b \cdot \log _b c=\log _a c$, the product simplifies:

$\left(\log _3 4\right)\left(\log _4 5\right)\left(\log _5 6\right)\left(\log _6 7\right)\left(\log _7 8\right)\left(\log _8 9\right)=\log _3 9$

$\log _3 9=\log _3\left(3^2\right)=2$

Q 2. Upto 500, how many numbers has distinct digits

Solution:

Case 1: 1-digit numbers
There are 1 -digit numbers from 1 to 9 (excluding 0 since 0 is not counted in the distinct digits range here): 9 numbers.

Case 2: 2-digit numbers
For a 2-digit number $A B$ :
- The first digit $A$ (tens place) has 9 choices (1 to 9 ).
- The second digit $B$ (units place) must be different from $A$, so it has 9 choices ( 0 to 9, excluding $A$ ).

Thus, $9 \times 9=81 \text { numbers }$

Case 3: 3-digit numbers less than 500
For a 3-digit number $A B C$, with $A$ as the hundreds place:
- $A$ can be $1,2,3$, or 4 (since the number must be less than 500 ). This gives 4 choices for $A$.
- $B$ (tens place) must be different from $A$, so it has 9 choices ( 0 to 9, excluding $A$ ).
- $C$ (units place) must be different from both $A$ and $B$, so it has 8 choices.

Thus, $4 \times 9 \times 8=288 \text { numbers }$

So, the total count of numbers up to 500 with distinct digits is $9+81+288=378$

Q 3. Avg of 3 numbers, is 28 when the largest is decreased by 10, smallest is increased by 7, Avg becomes 2 more than middle term Keeping the order unchanged, the Difference between largest and smallest number is now 64. Find the original largest number.

Solution:

Let a be the smallest, b be the middle and c be the largest number.

Average of $\mathrm{3}$ numbers is $\mathrm{2 8}$

$
\begin{aligned}
& \frac{a+b+c}{3}=28 \\
& a+b+c=84
\end{aligned}$

When the largest number is decreased by 10 and the smallest number is increased by 7, the new average becomes 2 more than the middle term:
- The new numbers are $a+7, b$, and $c-10$.
- The new average is:

$\frac{(a+7)+b+(c-10)}{3}=b+2$
Simplify the left-hand side:

$\frac{a+b+c-3}{3}=b+2$

Substitute $a+b+c=84$ :

$\begin{gathered}
\frac{84-3}{3}=b+2 \\
\frac{81}{3}=b+2 \\
27=b+2 \\
b=25
\end{gathered}$

The difference between the largest and smallest number after modifications is 64:
- The modified numbers are $a+7$ and $c-10$.
- The difference between them is:

$(c-10)-(a+7)=64$

Simplify:

$\begin{gathered}
c-a-17=64 \\
c-a=81
\end{gathered}$

Solve for $a$ and $c$

Substituting $b=25$ in $a+b+c=84$ :

$\begin{gathered}
a+25+c=84 \\
a+c=59
\end{gathered}$

We also have $c-a=81$.

Let's solve these two equations:
1. $a+c=59$
2. $c-a=81$

Add the two equations:

$\begin{gathered}
(a+c)+(c-a)=59+81 \\
2 c=140 \\
c=70
\end{gathered}$

Now substitute $c=70$ in $a+c=59$ :

$
\begin{gathered}
a+70=59 \\
a=-11
\end{gathered}$

The original largest number is c=70

Q 4. Gopi mark up the price by $\mathrm{2 0 \%}$, Ram gets $\mathrm{1 0 \%}$ discount thus saving Rs 15. Find Profit mode by Gopi?

Solution:

Let the cost price (C.P.) of the item be $x$.

Marked Price (M.P.)

Gopi marks up the price by $20 \%$ :

$\text { M.P. }=x+0.2 x=1.2 x$

Ram gets a $10 \%$ discount on the marked price:

$\text { S.P. }=1.2 x-0.1(1.2 x)=1.2 x-0.12 x=1.08 x$

The discount given to Ram is:

$\text { Discount }=\text { M.P. }- \text { S.P. }=1.2 x-1.08 x=0.12 x $

From the problem, Ram saves Rs 15 as the discount:

$0.12 x=15 \Longrightarrow x=\frac{15}{0.12}=125$

The cost price is $x=125$, and the selling price is:

$\text { S.P. }=1.08 x=1.08 \times 125=135$

Profit is the difference between the selling price and the cost price:

$\text { Profit = S.P. }- \text { C.P. }=135-125=10$

Q 5. Sum of all distinct values of $10^x+\frac{4}{10^x}=\frac{81}{2}$

Solution:

Let $y=10^x$. Then, the equation becomes:

$y+\frac{4}{y}=\frac{81}{2}$

$y^2+4=\frac{81}{2} y$

$2 y^2-81 y+8=0$

Use the quadratic formula:

$\begin{gathered}
y=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}, \quad a=2, b=-81, c=8 . \\
y=\frac{81 \pm \sqrt{81^2-4(2)(8)}}{2(2)} . \\
y=\frac{81 \pm \sqrt{6561-64}}{4} . \\
y=\frac{81 \pm \sqrt{6497}}{4} .
\end{gathered}$
Thus, the solutions for $y$ are:

$y_1=\frac{81+\sqrt{6497}}{4}, \quad y_2=\frac{81-\sqrt{6497}}{4} .$
Since $y=10^x$, the corresponding solutions for $x$ are:

$ x_1=\log _{10}\left(\frac{81+\sqrt{6497}}{4}\right), \quad x_2=\log _{10}\left(\frac{81-\sqrt{6497}}{4}\right)$

Using the property of logarithms:

$\log _{10}(a)+\log _{10}(b)=\log _{10}(a \cdot b)
$
Here, $a=\frac{81+\sqrt{6497}}{4}, \quad b=\frac{81-\sqrt{6497}}{4}$

The product $a \cdot b$ is:

$\begin{gathered}
a \cdot b=\frac{(81+\sqrt{6497})(81-\sqrt{6497})}{16} \\
a \cdot b=\frac{81^2-(\sqrt{6497})^2}{16} \\
a \cdot b=\frac{6561-6497}{16} \\
a \cdot b=\frac{64}{16}=4
\end{gathered}$

Thus, $\log _{10}(a)+\log _{10}(b)=\log _{10}(4)$

$\log _{10}(4)=\log _{10}\left(2^2\right)=2 \log _{10}(2)$.

Q 6. $|x+y|+|x-y|=2$ No. of pairs of $(\mathrm{x}, \mathrm{y})$ possible?

Solution: The absolute values $|x+y|$ and $|x-y|$ depend on the signs of $x+y$ and $x-y$. We consider the following cases:

Case 1: $x+y \geq 0$ and $x-y \geq 0$ :

$|x+y|=x+y, \quad|x-y|=x-y$

Substituting into the equation:

$(x+y)+(x-y)=2 \Longrightarrow 2 x=2 \Longrightarrow x=1$

Substituting $x=1$ into $x+y \geq 0$ and $x-y \geq 0$ :

$1+y \geq 0 \Longrightarrow y \geq-1, \quad 1-y \geq 0 \Longrightarrow y \leq 1$

So, $y \in[-1,1]$.

This gives 3 integer pairs: $(1,-1),(1,0),(1,1)$.

Case 2: $x+y \geq 0$ and $x-y \leq 0$ :

$|x+y|=x+y, \quad|x-y|=-(x-y)$

Substituting into the equation:

$(x+y)-(x-y)=2 \Longrightarrow 2 y=2 \Longrightarrow y=1$

Substituting $y=1$ into $x+y \geq 0$ and $x-y \leq 0$ :

$x+1 \geq 0 \Longrightarrow x \geq-1, \quad x-1 \leq 0 \Longrightarrow x \leq 1$

So, $x \in[-1,1]$.

This gives 3 integer pairs: $(-1,1),(0,1),(1,1)$.

Case 3: $x+y \leq 0$ and $x-y \geq 0$ :

$|x+y|=-(x+y), \quad|x-y|=x-y$
Substituting into the equation:

$-(x+y)+(x-y)=2 \Longrightarrow-2 y=2 \Longrightarrow y=-1$

Substituting $y=-1$ into $x+y \leq 0$ and $x-y \geq 0$ :

$x-1 \geq 0 \Longrightarrow x \geq 1, \quad x+(-1) \leq 0 \Longrightarrow x \leq 1$

So, $x=1$.

This gives 1 integer pair: $(1,-1)$.

Case 4: $x+y \leq 0$ and $x-y \leq 0$ :

$|x+y|=-(x+y), \quad|x-y|=-(x-y) $
Substituting into the equation:

$-(x+y)-(x-y)=2 \Longrightarrow-2 x=2 \Longrightarrow x=-1 $

Substituting $x=-1$ into $x+y \leq 0$ and $x-y \leq 0$ :

$-1+y \leq 0 \Longrightarrow y \leq 1, \quad-1-y \leq 0 \Longrightarrow y \geq-1$
So, $y \in[-1,1]$.

This gives 3 integer pairs: $(-1,-1),(-1,0),(-1,1)$.

However, some pairs are repeated:
- $(1,-1)$ appears in Cases 1 and 3.
- $(-1,1)$ appears in Cases 2 and 4.

Thus, there are:

$3+3+1+3-2=8 \text { distinct pairs }$

कैट 2024 स्लॉट 2 प्रश्न (स्मृति आधारित) (CAT 2024 Slot 2 Questions (Memory Based)

1. A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is

2. Find the remainder $3^333$ ÷ 11

3. When 2 liters of water is added to a mixture of acid and water, the concentration of acid becomes 50%. Then, 15 liters of acid is added to the solution, which makes the concentration of acid 80%. What is the quantity of the initial mixture?

4. If $\alpha$ and $\beta$ are the roots of the quadratic equation $x^2+p x+q=0$ find the value of $\left(\alpha^3+\beta^3\right)^2$

कैट 2024 स्लॉट 1 प्रश्न (स्मृति आधारित) (CAT 2024 Slot 1 Questions (Memory Based)

CAT 2024 परीक्षा का दोपहर का स्लॉट समाप्त होते ही यह अनुभाग अपडेट कर दिया जाएगा।

CAT 2024 Slot 1 QUANT Questions

1. Find the remainder of $\frac{100^{100}}{7}$

2. There are 187 fruits in a basket. The ratio of apples to mangoes is in the ratio 5:2. After selling 75 apples and 26 mangoes and half the number of oranges, the leftover apples and oranges was in the ratio 3:2.

Ans: 66

3. If $a_n$ represents the greatest integer function of $\sqrt{n}$, then sum of $a_1, a_2, a_3, \ldots a_{49}, a_{50}$ is?

Ans: 217

4. S.P of product is fixed to ensure 40% profit. If product cost 40% less, and have been sold for Rs. 5 less, Then Profit would have been 50%, then the original S.P is:

A) 5

B) 10

C) 20

D) 14

Ans: 14

5. A vessel is full of milk $2 / 3^{\text {rd }}$ of the milk is removed and replaced with water. This process is repeated 3 more times. Then find ratio of milk and water in the final solution.

6. $A B=56, C D=45$. Inradius of circle in ADE..

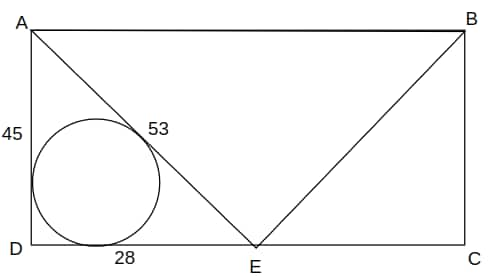
Ans: 10

7. Q. $(1 / 8)^k \times\left(1 / 8^{5}\right)^{1 / 3}=(1 / 8) x$ $\left(1 / 8^{5}\right)^{1 / k}$. Find the sum of all posslble values of ' $\mathbf{k}$ '

8. For any natural Number ' $n$ ', let an be the largest number not exceeding $\sqrt{\mathrm{n}}$, then $\mathrm{a_1}+\mathrm{a_2}+$ $a_3$... $+a_{50}$=

9. $x$ is a +ve real no,$
4 \operatorname{lox}_{10} x+4 \log _{100} x+
$ $8 \log { }_{1000} x=13$, then the greatest integer not exceeding ' $x$ '

10. $(1 / 8)^k \times\left(1 / 8^{5} \right)^{1 / 3}=(1 / 8) \times$ $\left(1 / 8^{5} \right)^{1 / k}$. Find the sum of all possible values of ' $\mathbf{k}$ '

11. Let $x, y, z$ be real numbers and $4\left(x^3+y^2+z^2\right)=a, 4(x-y-z)=3+a$, then find the value of ' a '

कैट स्लॉट 2 प्रश्न 2024 (स्मृति आधारित) (CAT Slot 2 Questions 2024 (Memory Based)

जल्द ही उपलब्ध कराए जायेंगे।

कैट स्लॉट 3 प्रश्न 2024 (स्मृति आधारित) (CAT 2024 Slot 3 Questions (Memory Based)

जल्द ही उपलब्ध कराए जायेंगे।

इस वर्ष कैट परीक्षा का संचालन आईआईएम कलकत्ता कर रहा है। कैट (कॉमन एडमिशन टेस्ट) 2024 में शामिल होने वाले छात्रों की कुल संख्या 3.29 लाख है। कैट 2024 परीक्षा 170 शहरों में 375+ केंद्रों पर तीन सत्रों में आयोजित की जाएगी। कैट 2024 परीक्षा परिणाम (CAT 2024 exam result) जनवरी 2025 के दूसरे सप्ताह में जारी होने की संभावना है।

कैट प्रश्न पत्र (CAT Question Papers)

कैट प्रश्न पत्र के माध्यम से उम्मीदवार कैट 2024 परीक्षा में उनके मजबूत और कमजोर क्षेत्रों को समझने में मदद करेगा और उनके समय प्रबंधन कौशल में काफी सुधार करेगा। कैट पिछले वर्ष के प्रश्न पत्रों में कैट पाठ्यक्रम से क्वॉंटिटेटिव एप्टिट्यूड, लॉजिकल रीज़निंग, रीडिंग कॉम्प्रिहेन्शन तथा वर्बल एबिलिटी विषयों से प्रश्न होंगे।

कैट प्रश्नों का उत्तर देने के लिए, व्यक्ति को क्रिटिकल थिंकिंग, विश्लेषणात्मक कौशल और इंटरप्रेट कॉम्प्लेक्स इन्फॉर्मेशन की क्षमता की आवश्यकता होती है। किसी छात्र के व्यावसायिक कौशल का आकलन करने के लिए कैट प्रश्न पत्र अक्सर वास्तविक जीवन से संबंधित मामले के अध्ययन और स्थितिजन्य प्रश्नों पर आधारित होते हैं। कैट के पिछले प्रश्न पत्रों के साथ अभ्यास करने से छात्रों को तैयारी में लाभ मिलेगी। हालाँकि, कैट प्रश्न पत्र आगामी कैट परीक्षा सत्र की सटीक जानकारी प्रदान करता है।

ये भी पढ़ें: समाधान सहित कैट प्रश्न पत्र सेट डाउनलोड करें

सॉल्यूशन पीडीएफ सहित कैट प्रश्न पत्र (1991-2023) (CAT Question Paper with Solution PDF (1991-2023)

कैट पिछले वर्ष के पेपर पीडीएफ (2017-2023) (CAT Previous Year Paper PDF (2017-2023)

पिछले वर्ष के कैट प्रश्न पत्रों की मदद से कैट परीक्षा पैटर्न, उच्च वेटेज वाले विषयों और कठिन कैट प्रश्नों के प्रकारों को समझना संभव है। इस पृष्ठ पर नीचे स्लॉट-वार पिछले 6 वर्षों (2017 से 2023) के कैट प्रश्न पत्र डाउनलोड करें। इसके अलावा, परीक्षा का अनुमान लगाने के लिए आधिकारिक कैट मॉक टेस्ट भी देखें।

कैट पिछले वर्ष प्रश्न पत्र उत्तर सहित- स्लॉट-वार (CAT Previous Year Question Paper with Answers- Slot-wise)

कैट परीक्षा को तीन खंडों में विभाजित किया गया है: वर्बल एबिलिटी एंड रीडिंग कॉम्प्रिहेन्शन (वीएआरसी), डेटा इंटरप्रेटेशन एंड लॉजिकल रीज़निंग (डीआईएलआर), और क्वॉंटिटेटिव एबिलिटी (क्यूए)। अनुभाग-वार कैट पिछले वर्ष के पेपर डाउनलोड करें।

कैट प्रश्न पत्र 2022 पीडीएफ

• कैट 2022 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2022 वीएआरसी अनुभाग (स्लॉट 2)
• कैट 2022 वीएआरसी अनुभाग (स्लॉट 3)
• कैट 2022 डीआईएलआर (स्लॉट 1)
• कैट 2022 डीआईएलआर (स्लॉट 2)
• कैट 2022 डीआईएलआर (स्लॉट 3)
• कैट 2022 क्वांट सेक्शन (स्लॉट 1)
• कैट 2022 क्वांट सेक्शन (स्लॉट 2)
• कैट 2022 क्वांट सेक्शन (स्लॉट 3)

कैट 2021 प्रश्न पत्र सेक्शन वाइज पीडीएफ

• कैट 2021 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2021 वीएआरसी सेक्शन (स्लॉट 2)
• कैट 2021 वीएआरसी सेक्शन (स्लॉट 3)
• कैट 2021 डीआईएलआर (स्लॉट 1)
• कैट 2021 डीआईएलआर (स्लॉट 2)
• कैट 2021 डीआईएलआर (स्लॉट 3)
• कैट 2021 क्वांट सेक्शन (स्लॉट 1)
• कैट 2021 क्वांट सेक्शन (स्लॉट 2)
• कैट 2021 क्वांट सेक्शन (स्लॉट 3)

कैट 2020 प्रश्न पत्र पीडीएफ अनुभाग वार

• कैट 2020 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2020 वीएआरसी सेक्शन (स्लॉट 2)
• कैट 2020 वीएआरसी सेक्शन (स्लॉट 3)
• कैट 2020 डीआईएलआर (स्लॉट 1)
• कैट 2020 डीआईएलआर (स्लॉट 2)
• कैट 2020 डीआईएलआर (स्लॉट 3)
• कैट 2020 क्वांट सेक्शन (स्लॉट 1)
• कैट 2020 क्वांट सेक्शन (स्लॉट 2)
• कैट 2020 क्वांट सेक्शन (स्लॉट 3)

कैट पिछले वर्ष के प्रश्न 2019

• कैट 2019 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2019 वीएआरसी सेक्शन (स्लॉट 2)
• कैट 2019 डीआईएलआर (स्लॉट 1)
• कैट 2019 डीआईएलआर (स्लॉट 2)
• कैट 2019 क्वांट सेक्शन (स्लॉट 1)
• कैट 2019 क्वांट अनुभाग (स्लॉट 2)

कैट 2018 प्रश्न पत्र पीडीएफ अनुभाग वार

• कैट 2018 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2018 वीएआरसी सेक्शन (स्लॉट 2)
• कैट 2018 डीआईएलआर (स्लॉट 1)
• कैट 2018 डीआईएलआर (स्लॉट 2)
• कैट 2018 क्वांट सेक्शन (स्लॉट 1)
• कैट 2018 क्वांट सेक्शन (स्लॉट 2)

कैट 2017 प्रश्न पत्र अनुभाग वार पीडीएफ

• कैट 2017 वीएआरसी सेक्शन (स्लॉट 1)
• कैट 2017 वीएआरसी सेक्शन (स्लॉट 2)
• कैट 2017 डीआईएलआर (स्लॉट 1)
• कैट 2017 डीआईएलआर (स्लॉट 2)
• कैट 2017 क्वांट सेक्शन (स्लॉट 1)
• कैट 2017 क्वांट सेक्शन (स्लॉट 2)

कैट पिछला वर्ष प्रश्न पत्र पीडीएफ मुफ्त डाउनलोड

• वर्ष और स्लॉट के अनुसार कैट प्रश्न पत्र पीडीएफ लिंक पर क्लिक करें
• कैट परीक्षा प्रश्न पत्र पीडीएफ डाउनलोड करें
• कैट के पिछले प्रश्न पत्रों को सेव और स्टार्ट करें

कैट प्रश्नों को हल करना कैट टॉपर्स के लिए सफलता के प्रमुख मंत्रों में से एक है। बेहतर कैट परीक्षा की तैयारी के लिए कैट 2024 के लिए एक साल की अध्ययन योजना देखें और कैट 2024 के लिए सर्वोत्तम अध्ययन सामग्री कैट 2024 के लिए सर्वोत्तम अध्ययन सामग्री जानें।

कैट प्रश्न पत्र - अवलोकन (CAT Question Paper - Overview)

कैट 2024 को क्रैक करने के लिए कैट पैटर्न को समझना महत्वपूर्ण है। उम्मीदवारों कैट परीक्षा पैटर्न 2024 को जान कर, परीक्षा की तैयारी बेहतर तरीके से कर सकते हैं तथा उन्हें यह जानने में मदद मिलेगी कि परीक्षा में क्या उम्मीद की जानी चाहिए।

कैट स्कोर बनाम परसेंटाइल 2024 (संभावित) (CAT Score vs Percentile 2024 (Expected)

कैट पिछले वर्ष के प्रश्न-पत्र (CAT Previous Year Paper)

कैट परीक्षा में शामिल विषयों में कॉम्प्रिहेन्शन-आधारित प्रश्न, संख्या प्रणाली से संबंधित प्रश्न और पज़ल शामिल हैं। कैट पेपर का उद्देश्य उम्मीदवार की क्रिटिकल थिंकिंग क्षमता, समस्या-समाधान कौशल और समय प्रबंधन कौशल का परीक्षण करना है। परीक्षा में उत्कृष्ट अंक प्राप्त करने के लिए उम्मीदवारों के लिए सावधानीपूर्वक तैयारी करना और विभिन्न मॉक टेस्ट का अभ्यास करना आवश्यक है।

कैट मॉक टेस्ट लिंक

मॉक टेस्ट में पिछले वर्षों के कॉमन एडमिशन टेस्ट (CAT) के पेपर से चुने हुए प्रश्न शामिल हैं, जिसका उद्देश्य उम्मीदवारों को कैट में आमतौर पर पूछे जाने वाले विभिन्न प्रकार के प्रश्नों (MCQs/ Non-MCQs) और परीक्षा इंटरफ़ेस से परिचित कराना है। दिए गए मॉक टेस्ट को पिछले वर्ष अपनाए गए पैटर्न के आधार पर गैर-PwD उम्मीदवार के लिए कुल 120 मिनट (तीन खंडों के लिए प्रत्येक 40 मिनट) की अवधि के साथ डिज़ाइन किया गया है। इस मॉक टेस्ट का उद्देश्य CAT 2024 के लिए परीक्षा पैटर्न का खुलासा करना नहीं है और प्रश्नों की संख्या, प्रकार और पैटर्न, साथ ही मॉक परीक्षा में अनुभागों का क्रम और समय केवल सांकेतिक हैं और ये कैट अधिकारियों द्वारा तय किए गए वर्ष-दर-वर्ष बदलाव के अधीन हैं।

कंसोर्डियम ने कहा है कि उम्मीदवार कृपया ध्यान दें कि कैट 2024 में गैर-PwD उम्मीदवार के लिए कुल 120 मिनट (तीन खंडों के लिए प्रत्येक 40 मिनट) की अवधि होगी। PwD उम्मीदवारों को 40 मिनट अतिरिक्त दिए जाएंगे। मॉक लिंक के प्रत्येक अनुभाग के लिए सबमिट बटन है। यह उम्मीदवार को 40 मिनट का आवंटित समय समाप्त होने से पहले ही अगले अनुभाग में जाने में मदद करने के लिए है। वास्तविक परीक्षा में, उम्मीदवार 40 मिनट के बाद ही अगले सेक्शन में जा सकता है। इस दस्तावेज़ के किसी भी भाग को किसी भी रूप में या किसी भी माध्यम से [ग्राफ़िक, इलेक्ट्रॉनिक या मैकेनिकल, जिसमें फोटोकॉपी, रिकॉर्डिंग, टेपिंग या सूचना पुनर्प्राप्ति प्रणाली शामिल है] पुन: प्रस्तुत या कॉपी नहीं किया जा सकता है या किसी डिस्क, टेप, अन्य मीडिया या अन्य सूचना भंडारण उपकरणों आदि पर पुन: प्रस्तुत नहीं किया जा सकता है।
कैट 2024 मॉक टेस्ट लिंक | कैट 2024 मॉक टेस्ट लिंक पीडब्ल्यूडी (अंधापन और कम दृष्टि) उम्मीदवारों के लिए | कैट 2024 मॉक टेस्ट लिंक पीडब्ल्यूडी उम्मीदवारों के लिए

कैट प्रश्न - आधिकारिक कैट मॉक टेस्ट लिंक (CAT Questions - Official CAT Mock Test Links)

कैट प्रश्न पत्र: रीडिंग कॉम्प्रिहेन्शन के लिए विषय (CAT Question Papers: Topics for Reading Comprehension)

कैट प्रश्न पत्र - महत्वपूर्ण विषय (CAT Question Paper - Important Topics)

कैट पेपर में तीन सेक्शन होते हैं: वर्बल एबिलिटी एंड रीडिंग कॉम्प्रिहेन्शन, डेटा इंटरप्रेटेशन एंड लॉजिकल रीज़निंग, और क्वॉंटिटेटिव एप्टिट्यूड। कैट प्रश्न छात्रों के विश्लेषणात्मक, तार्किक और समझ कौशल का परीक्षण करते हैं। कैट पेपर में बहुविकल्पीय प्रश्नों और गैर-बहुविकल्पीय प्रश्नों का मिश्रण होता है। कुछ प्रश्न केस स्टडीज, ग्राफ़ और डेटा इंटरप्रेटेशन पर आधारित होते हैं।

इसलिए महत्वपूर्ण विषय जो कैट के पिछले वर्षों के प्रश्नपत्रों का भाग रहे हैं, बेहतर तैयारी और अच्छा स्कोर करने के लिए उपयोगी हैं। उम्मीदवार कैट 2024 तैयारी सामग्री का उपयोग करके कैट 2024 में 100 परसेंटाइल प्राप्त कर सकते हैं।

पिछले वर्ष के क्यूए अनुभाग से कैट प्रश्न के विषय (QA Topics from Past CAT Question Papers)

पिछले वर्ष के वीएआरसी अनुभाग से कैट प्रश्न के विषय (VARC Topics from CAT Previous Question Papers)

पिछले वर्ष के डीआईएलआर अनुभाग से कैट प्रश्न के विषय (DILR Important Topics Based on CAT Question Papers)

पिछले वर्षों के कैट पेपर के क्या लाभ हैं? (What are the advantages of CAT Previous Years Papers)

क्या पिछले वर्षों के कैट प्रश्नपत्रों को हल करना महत्वपूर्ण है? जी हां, यह बेहद ही जरूरी है। उम्मीदवारों को अपनी तैयारी के दौरान और वास्तविक कैट परीक्षा से पहले कैट के पिछले वर्ष के प्रश्न पत्रों को हल करने से बहुत लाभ होगा। कैट प्रश्नपत्र हल करने के फायदे इस प्रकार हैं:

• समय प्रबंधन
• उत्तर देने में गति में वृद्धि और सटीकता
• वेटेज के साथ विषयों का पृथक्करण
• आसान समस्या-समाधान तकनीक
• कैट प्रश्नों को हल करने के सामान्य सूत्र

कैट प्रश्न पत्रों का अभ्यास कब शुरू करें? (When to Start Practicing CAT Question Papers?)

कैट परीक्षा के पिछले वर्ष के प्रश्नपत्रों को हल करने से उम्मीदवारों को यह पता चल जाता है कि उन्होंने किस सेक्शन के लिए अच्छी तैयारी की है और उन्हें किस सेक्शन पर काम करने की ज़रूरत है। यदि कोई उम्मीदवार सब कुछ नए सिरे से शुरू कर रहा है, तो उसे कैट के पिछले वर्ष के पेपर पर एक नजर डालने की सलाह दी जाती है। यह कैट परीक्षा पैटर्न से परिचित होने के लिए है। लेकिन किसी को भी तैयारी से पहले उन्हें हल करना शुरू नहीं करना चाहिए क्योंकि यह उपयोगी साबित नहीं होगा।

कैट 2024 पाठ्यक्रम और विषयों पर अच्छी तरह से नज़र डालने के बाद, उम्मीदवार अपनी तैयारी शुरू कर सकते हैं। प्रत्येक अध्याय और विषय के पूरा होने के साथ, कैट प्रश्नों को हल करके तैयारी के स्तर का परीक्षण करना महत्वपूर्ण है। मॉक टेस्ट और कैट के पिछले वर्ष के प्रश्न पत्र इसके लिए सही उपकरण हैं।

कैट टॉपर्स और कैट सलाहकार कैट की तैयारी के दौरान कम से कम 30-40 मॉक टेस्ट हल करने की सलाह देते हैं। कुछ टॉपर्स 80 मॉक टेस्ट तक भी प्रयास करते हैं।