TS ICET 2025 Mathematical Ability Sample Questions (Section-wise) - Download Free PDF

TS ICET Mathematical Ability Sample Questions 2025: On June 8 and 9, the much-awaited TS ICET examination will be conducted. More than 75,000 candidates appeared for the TS ICET 2024 examination. The number of candidates is expected to increase this year. The exam will be conducted in 4 slots, with 2 slots happening on a day. The overall difficulty level of the TS ICET examination is expected to be easy to moderate. All the candidates seeking admission to MCA and MBA degrees in various public and private colleges in Telangana must appear for the TS ICET examination. The mathematical ability of the TS ICET examination is considered to be one of the most challenging sections of the examination. 75 questions are asked from this section alone. Also, both time constraints and lengthy questions add to the difficulty of the mathematical ability section of the TS ICET examination. The most effective method of preparing for the TS ICET’s mathematical ability section is through practice. To gain practice, the candidates must solve a good number of TS ICET ability sample questions. Since there are a lot of possible topics from which the questions can be asked, the candidates should solve the TS ICET mathematical ability model questions to prepare themselves for the TS ICET exam day.

New: TS ICET 2025 Preparation Tips

Latest: TS ICET 2025 Sample Papers with Solutions

Admission Alert: MBA @ GITAM School of Business

This Story also Contains

1. TS ICET 2025 Exam Pattern
2. TS ICET Mathematical Ability Overview
3. TS ICET Mathematical Ability Sample Questions: Arithmetical Ability
4. TS ICET Mathematical Ability Sample Questions: Algebraic and Geometric Ability
5. TS ICET Mathematical Ability Sample Questions: Statistical Ability
6. TS ICET 2025 Preparation Plan for 2 Months
7. Best Books for TS ICET 2025

TS ICET 2025 Exam Pattern

According to the Telangana State Council of Higher Education (TSCHE), which is responsible for conducting the TS ICET 2025 examination, there is no change in the TS ICET exam pattern for this year. Hence, the candidates can expect the same trends of the previous year as far as the TS ICET examination is concerned. Given below is the official TS ICET exam pattern.

TS ICET Mathematical Ability Overview

The second section, or section B of the TS ICET question paper, will be the mathematical ability section. The number of questions under the mathematical ability section of the TS ICET 2025 question paper will be divided into three sections: the arithmetic section, algebraic and geometric ability, and statistical ability. The question paper will be arithmetic-dominated, while the statistical ability section will have the least number of questions. The overview and the question distribution of the TS ICET mathematical ability section are given below:

TS ICET Mathematical Ability Sample Questions: Arithmetical Ability

As mentioned before, the arithmetical ability section of the TS ICET examination holds the maximum weightage in the mathematical ability section of the TS ICET 2025 question paper. This accounts for almost 47% of the total questions. Hence, the arithmetic section must be given the highest priority during the candidate’s TS ICET mathematical ability preparation. A few of the TS ICET mathematical ability sample questions under the arithmetic section are listed below.

1. The LCM of x2 − 8x + 15 and x2 − 5x + 6 is:

1. (x - 2) (x - 3) (x − 5)

2. (x − 6)2 (x + 1) (x − 3)

3. (x − 6) (x + 1) (x − 3)

4. (x+6) (x+1) (x-3)

Correct Answer: A

x2 − 8x + 15 = (x – 3)(x – 5)

x2 − 5x + 6 = (x – 2)(x – 3)

So, LCM (x2 − 8x + 15, x2 − 5x + 6) = LCM((x – 3)(x – 5), (x – 2)(x – 3))

= (x - 2) (x - 3) (x − 5)

Hence, the answer is (x - 2) (x - 3) (x − 5).

2. If a 4-digit number x58y is exactly divisible by 9, then the least value of (x + y) is:

1. 4

2. 5

3. 3

4. 2

Correct Answer: B

A number is divisible by 9 if the sum of its digits is divisible by 9.

Given a 4-digit number x58y, the sum of its digits is x + 5 + 8 + y = (x + y) + 13.

For the number to be divisible by 9, (x + y) + 13 must be divisible by 9.

The smallest possible value for (x + y) that makes (x + y) + 13 divisible by 9 is 5 (since 5 + 13 = 18, and 18 is the multiple of 9).

Hence, the answer is 5.

3. What is the ratio between the HCF and LCM of the numbers whose LCM is 48 and the product of the numbers is 384?

1. 1 : 4

2. 1 : 6

3. 1 : 3

4. 2 : 5

Correct Answer: B

Let the HCF be a.

We know that,

HCF × LCM = Product of two numbers

⇒ 48 × a = 384

⇒ a = 384/48

⇒ a = 8

HCF : LCM = 8 : 48

= 1 : 6

Hence, the correct answer is 1 : 6.

4. When a number is increased by 112, it becomes 170% of itself. Find the number.

1. 160

2. 150

3. 200

4. 180

Correct Answer: A

Let the number be x

According to the question,

x + 112 = x × (170/100)

=> 10x + 1120 = 17x

=> 7x = 1120

=> x = 160

5. Sonam bought an old motorbike for Rs. 4675 and spent Rs. 225 on its repair. Then she sold it in Rs. 5390 . What is her profit percent?

1. 20%

2. 15%

3. 10%

4. 8%

Correct Answer: C

Given: Sonam bought an old motorbike for Rs. 4675 Spent on repairing = Rs. 225 Cost price = 4675 + 225 = 4900 Selling Price = Rs. 5390

Profit percent = (Selling price - Cost price) / Cost price × 100

Profit percent = (5390 - 4900) / 4900 × 100

Profit percent = 490 / 4900 × 100

Profit percent = 10

6. X, Y and Z enter into a partnership. X invests some money at the beginning. Y invests thrice the amount of X after 4 months and Z invest double the amount of Y after 9 months from the beginning. If the annual gain is INR 450000, then what is the share of Y?

1. INR 200000

2. INR 150000

3. INR 100000

4. INR 300000

Correct Answer: A

Let x be the amount invested by X.

Investment ratio

= x×12 : 3x×8 : 6x×3

= 12 : 24 : 18

= 2 : 4 : 3

Profit ratio = investment ratio = 2:4:3

Total gain = INR 450000

Share of Y = (4 / (2 + 4 + 3)) × 450000

= 4 × 50000

= INR 200000

Hence, the answer is INR 200000.

7. A man takes 20 hours to go to a place and come back by walking both ways. He could have saved 4 hours by riding both ways. The distance covered in the whole journey is 36 miles. Find the average speed for the whole journey if he goes by walking and comes back by riding.

1. 2 miles/hr

2. 1 miles/hr

3. 4 miles/hr

4. 3 miles/hr

Correct Answer: A

Average speed = Distance / Time

Based on the explanation provided:

The total time spent for both trips is 20 hours.

Walking one way at a steady speed takes 5 hours (since 10/2 = 5 hours).

The total time walking both ways is 10 hours, and the remaining 2 hours is due to the gain from riding.

The total time spent riding both ways is calculated as 10 - 8 = 2 hours.

The total distance is calculated as 18 miles. So the final step is using the average speed formula:

Average speed = Distance / Time

= 18 miles / 9 hours

= 2 miles per hour

Hence, the correct answer is 2 miles/hr.

TS ICET Arithmetic Ability Preparation Tips

Questions are asked from various topics under the TS ICET arithmetic ability section. This includes number systems, time, speed and distance, time and work, mensuration, surds and indices and so on. Since the syllabus is long, many candidates get disheartened and tend to lose focus midway through the TS ICET 2025 preparation. The candidates can incorporate a few strategies to stay ahead of the curve and prepare for the TS ICET 2025 examination’s mathematical ability. A few are listed below.

• While preparing for the TS ICET’s mathematical ability section, understanding the basics is of utmost importance. Without clarity in concepts, the candidates can often get confused, and this may lead to wrong answers. The candidates should start by strengthening their fundamentals in topics like percentages, profit and loss, simple and compound interest, time and work, and time, speed and distance.

• Since the mathematical ability section consumes the most time in the TS ICET examination, it is beneficial for the candidates to practice mental maths techniques to improve their calculation speed. This includes practising Vedic maths, remembering tables up to 20, and memorising square/cube values.

• The candidates are also advised to learn shortcut methods for solving arithmetic problems to save time during the exam.

• TS ICET previous year question papers are one of the finest resources for understanding the question types and difficulty levels. As soon as the candidates complete their TS ICET syllabus, they must start with the practice through the TS ICET previous year question papers.

• The candidates should also refer to good TS ICET books, practice or online platforms that offer chapter-wise tests and TS ICET mock exams to enhance their practice.

• Since this section requires more time to practice, the candidates should spend at least 30-45 minutes on their TS ICET mathematical ability practice.

TS ICET Mathematical Ability Sample Questions: Algebraic and Geometric Ability

1. Let A = {1, 3, 4, 6, 9} and B = {2, 4, 5, 8, 10}. Let R be a relation defined on A × B such that

R = {((a₁, b₁), (a₂, b₂)) : a₁ ≤ b₂ and b₁ ≤ a₂}.

Then the number of elements in the set R is ___.

1. 52

2. 160

3. 26

4. 180

Correct Answer: A

Relation, Number of Relation –

A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A × B.
The subset is formed by describing the relationship between the first element and the second element of the ordered pairs in A × B.

The second element is called the image of the first element.
If the element (a, b) belongs to R (where a belongs to A and b belongs to B), then the relation is represented as a R b.

Number of Relations from A to B:
If A has m elements and B has n elements, then A × B has m × n elements.
As the number of subsets of A × B is 2ᵐⁿ, and a relation is a subset of A × B, the total number of relations from A to B will be 2ᵐⁿ.

2. Let p(x) be a quadratic polynomial such that p(0)=1. If p(x) leaves remainder 4 when divided by (x−1) and it leaves remainder 6 when divided by (x+1); then :

1. p(2) = 11

2. p(2) = 19

3. p(−2) = 19

4. p(−2) = 11

Remainder theorem

The remainder theorem states that if a polynomial f(x) is divided by a linear function (x - k), then the remainder is f(k).

In Division,

Dividend = Divisor x Quotient + Remainder

For polynomials also we can use this theorem

f(x) = d(x).q(x) + r(x)

where f(x) is the divisor, d(x) is the divisor, q(x) is the quotient and r(x) is the remainder. And these 4 are polynomials

The degree of remainder r(x) is always less than the degree of divisor d(x)

Now, if divisor d(x) is a linear polynomial (x-k). Let q(x) be the quotient, and remainder r(x) will be a constant value equal to R:

f(x) = (x - k)q(x) + R

Now if we put x = k

i.e. f(k) = (k - k)q(x) + R = 0 + R

f(k) = R

So, remainder is f(k), when f(x) is divided by a linear polynomial (x-k)

3. If x = √(–√3 + √(3 + 8√(7 + 4√3))) where x > 0, then the value of x is equal to:

1. 3

2. 4

3. 1

4. 2

Correct Answer: D

Given: x = √(–√3 + √(3 + 8√(7 + 4√3))) where x > 0
We use the algebraic identity: (a + b)² = a² + b² + 2ab

⇒ x = √(–√3 + √(3 + 8√(4 + 3 + 4√3)))
⇒ x = √(–√3 + √(3 + 8√((2 + √3)²)))
⇒ x = √(–√3 + √(3 + 8(2 + √3)))
⇒ x = √(–√3 + √(3 + 16 + 8√3))
⇒ x = √(–√3 + √((4 + √3)²))
⇒ x = √(–√3 + 4 + √3)
Therefore, x = √4 = 2

Answer: 2

4. Find the value of the given expression:

√(8 + √1681)

1. 7

2. 1

3. 2

4. 3

Correct Answer: A

Solution:
√(8 + √1681)
= √(8 + 41)
= √49
= 7

Hence, the correct answer is 7.

4. △ABC is an equilateral triangle with a side of 12 cm and AD is the median. Find the length of GD if G is the centroid of △ABC.

1. 2√3

2. 2√4

3. 5√3

4. 10√3

Correct Answer: A

Solution:
Given: △ABC is an equilateral triangle with side 12 cm and AD is the median.
The height of an equilateral triangle = (√3 / 2) × side
So, height AD = (√3 / 2) × 12 = 6√3 cm

The centroid divides the median in the ratio 2 : 1.
Let AG = 2x and GD = x, so AD = 3x.

Now,2√3
3x = 6√3
⇒ x = 2√3 cm
⇒ GD = 2√3 cm

Hence, the correct answer is 2√3 cm.

5. The exterior angles obtained on producing the base of a triangle both ways are 121° and 104°. What is the measure of the largest angle of the triangle?

1. 80°

2. 70°

3. 76°

4. 45°

Correct Answer: C

Solution:
First exterior angle = 121°
Second exterior angle = 104°

The sum of all the exterior angles of a triangle is 360°.
Let the third exterior angle be x.

121° + 104° + x = 360°
x = 360° - 225° = 135°

Now, the interior angle corresponding to the smallest exterior angle will be the largest interior angle.
Smallest exterior angle = 104°
So, the largest interior angle = 180° - 104° = 76°

Hence, the correct answer is 76°.

6. A cyclic quadrilateral ABCD is such that AB = BC, AD = DC and AC and BD intersect at O. If angle CAD = 46°, then the measure of angle AOB is equal to:

1. 67°

2. 32°

3. 15°

4. 90°

Correct Answer: D

Solution:
Given:

• AB = BC

• AD = DC

• ABCD is a cyclic quadrilateral

• AC and BD intersect at O

• ∠CAD = 46°

Since AD = DC, triangle ADC is isosceles.
⇒ ∠CAD = ∠DCA = 46°
So, ∠ADC = 180° – (46° + 46°) = 88°

In a cyclic quadrilateral, opposite angles are supplementary.
⇒ ∠ABC = 180° – ∠ADC = 180° – 88° = 92°

Since AB = BC, triangle ABC is also isosceles.
⇒ ∠BAC = ∠BCA = (180° – 92°)/2 = 44°

Now, considering triangle AOB:
∠ABO = ∠DCA = ∠DAC = 46° (angles subtended by the same arc)
∠BAO = ∠BCA = 44°
Therefore, ∠AOB = 180° – (46° + 44°) = 90°

Hence, the correct answer is 90°.

7. The sum of the first 15 terms in an arithmetic progression is 200, while the sum of the next 15 terms is 350. Then the common difference is

1. 7/9

2. 1/3

3. 4/9

4. 2/3

Correct Answer: D

The sum of the first 15 terms of an arithmetic progression is given by:
S₁₅ = 200
Also, the sum of the next 15 terms (i.e., terms 16 to 30) is given as:
S₃₀ – S₁₅ = 350
Find the common difference d.

Solution:
We know the formula for the sum of the first n terms of an AP:
Sₙ = (n/2)[2a + (n – 1)d]

Given:
S₁₅ = (15/2)[2a + 14d] = 200
⇒ 2a + 14d = (200 × 2)/15 = 80/3
⇒ a + 7d = 40/3 -------- (1)

Sum of next 15 terms:
S₃₀ − S₁₅ = (30/2)[2a + 29d] − (15/2)[2a + 14d] = 350
⇒ 15[2a + 29d] − 15/2[2a + 14d] = 350
⇒ (15/2)[(2a + 29d) − (2a + 14d)] = 350
⇒ (15/2)(15d) = 350
⇒ (225d)/2 = 350
⇒ d = (350 × 2)/225 = 700/225 = 14/4.5 = 28/9 = 2/3

Hence, the correct answer is d = 2/3.

8. The 3rd, 14th and 69th terms of an arithmetic progression form three distinct and consecutive terms of a geometric progression. If the next terms of the geometric progression is the nth term of the arithmetic progression, then n equals._________

1. 344

2. 345

3. 346

4. 342

Correct Answer: A

Let the AP be:

• T₃ = a + 2d

• T₁₄ = a + 13d

• T₆₉ = a + 68d

These three are in G.P., so by property of G.P.,
(First term) × (Third term) = (Second term)²
⇒ (a + 2d)(a + 68d) = (a + 13d)²

Expanding both sides:
LHS: a² + 68ad + 2ad + 136d² = a² + 70ad + 136d²
RHS: a² + 26ad + 169d²

Equating both sides:
a² + 70ad + 136d² = a² + 26ad + 169d²
⇒ 44ad = 33d²
⇒ a/d = 3/4

Now let a = 3x and d = 4x.

Now, the common ratio r of the G.P. is:
r = (a + 13d) / (a + 2d)
= (3x + 52x) / (3x + 8x) = 55x / 11x = 5

So, the next term in the G.P. will be:
G₄ = G₃ × r = (a + 68d) × 5 = (3x + 272x) × 5 = 275x × 5 = 1375x

Now find the position n of 1375x in the AP:
Tₙ = a + (n − 1)d = 3x + (n − 1)(4x) = 1375x
⇒ 3x + 4x(n − 1) = 1375x
⇒ 4x(n − 1) = 1372x
⇒ n − 1 = 343
⇒ n = 344

Hence, the next term of the G.P. is the 344th term of the AP.

9. Question:
If sec θ + tan θ = 3, then what is the value of sec θ?

Options:
A. 4/3
B. 3/4
C. 3/5
D. 5/3

Correct Answer: D

Solution:
Given:
sec θ + tan θ = 3 — (1)

We know the identity:
If sec θ + tan θ = x, then sec θ − tan θ = 1/x

So, from (1),
sec θ − tan θ = 1/3 — (2)

Now, adding equations (1) and (2):
(sec θ + tan θ) + (sec θ − tan θ) = 3 + 1/3
⇒ 2 sec θ = 10/3
⇒ sec θ = 5/3

Correct Answer: D. 5/3

10. From the top of a hill 240 m high, the angles of depression of the top and bottom of a pole are 30° and 60°, respectively. The difference (in m) between the height of the pole and its distance from the hill is:

A. 120 × (2 − √3)

B. 120 × (√3 − 1)

C. 80 × (√3 − 1)

D. 80 × (2 − √3)

Correct Answer: D

Solution:

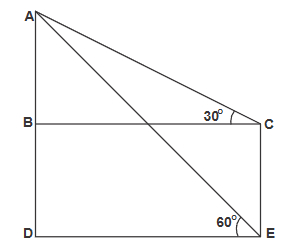
In △ADE:
⇒ tan 60° = AD / DE
⇒ √3 = 240 / DE
⇒ DE = 80√3

In △ABC:
⇒ tan 30° = AB / BC
⇒ 1/√3 = AB / BC
⇒ BC = AB√3

From the figure: BC = DE = 80√3
⇒ 80√3 = AB√3
⇒ AB = 80 m

Height of pole BD = AD − AB = 240 − 80 = 160 m

Required difference = 160 − 80√3 = 80(2 − √3)

TS ICET Algbraic and Geometry Preparation Tips

The algebraic and geometry section of the TS ICET question paper will consist of questions from topics such as height and distance, Arithmetic Progressions, Trigonometry and so on. The questions from this section can only be answered with proper practice of the TS ICET mathematical ability sample questions. A few TS ICET preparation tips under the algebraic and geometry sections are mentioned below.

• While preparing for the TS ICET section’s algebraic and geometry topics, the candidates should start with the algebra topic. They should focus on topics such as linear equations, quadratic equations, polynomials, and algebraic identities. As time passes, the candidates should solve more TS ICET mathematical ability model questions and practice simplifying and solving equations quickly.

• Later, the candidates should move on to the topics such as properties of basic shapes (triangles, circles, quadrilaterals) and important theorems related to angles, lines, and areas.

• There will be a lot of formulas related to different concepts of algebra and geometry. The candidates will have to go through each of them and memorise it. To make the preparation easier, the candidates can also keep a small notebook where they can write down the various formulas for easy and quick reference.

• One important tip is that the candidates should solve concept-based questions more. This would help them to solidify their understanding of the concepts rather than testing their memorisation of concepts. This would be beneficial for the candidates to learn the concepts and solve the different questions that come from the same concept.

TS ICET Mathematical Ability Sample Questions: Statistical Ability

With the questions on statistical ability, the mathematical ability section of the TS ICET examination will conclude. The candidates will be required to answer 10 questions from this section. This section will include questions from basic central tendencies such as mean, median and mode, followed by questions from probability. A set of TS ICET sample questions that the candidates can learn from the TS ICET Mathematical ability section’s statistical ability is listed below.

1. The mode of the following data is __________.

13, 15, 31, 12, 27, 13, 27, 30, 27, 28 and 16

1. 28

2. 27

3. 30

4. 31

Correct Answer: B

Mode is the most appearing data in a given dataset.

Given dataset: 13, 15, 31, 12, 27, 13, 27, 30, 27, 28 and 16

Here, 27 appears 3 times, which is the most.

So, the mode is 27.

Hence, the correct answer is 27.

2. The median of the following data will be _________.

32, 25, 33, 27, 35, 29, and 30

1. 32

2. 27

3. 30

4. 29

Correct Answer: C

First, arrange the data in ascending order:
25, 27, 29, 30, 32, 33, 35

Since the number of terms is odd (7 terms), the median is the middlemost term:
Position of the median = (7 + 1) / 2 = 4th term

⇒ Median = 30

3. The arithmetic mean of the following data is _________.

23, 17, 20, 19, 21

1. 20

2. 10

3. 30

4. 25

Correct Answer: A

Solution:

Arithmetic mean = Sum of observations ÷ Number of observations

= (23 + 17 + 20 + 19 + 21) ÷ 5

= 100 ÷ 5

= 20

4. The median of a set of 11 distinct observations is 73.2. If each of the largest five observations of the set is increased by 3, then the median of the new set__________.

1. is 3 times that of the original set

2. is increased by 3

3. remains the same as that of the original set

4. is decreased by 3

Correct Answer: C

Solution:

Median of a set with n observations is the value at the position:

Median = [ (n + 1) / 2 ]ᵗʰ observation (when n is odd).

Since only the largest 5 observations are increased by 3, and the 6th observation or middle value (which determines the median) remains unchanged, the median also remains unchanged.

5. Find the mode for the given distribution (rounded off to two decimal places).

1. 28.33

2. 7.23

3. 12.87

4. 30.01

Solution:

Here, the maximum frequency is 11, and the corresponding class is 25 to 30.
So the modal class is 25 to 30.
Now, the lower limit of the modal class (l) is 25,
Frequency of the modal class (f1) is 11
Frequency of the class before the modal class (f0) is 9
Frequency of the class after the modal class (f2) is 10
Class size (h) is 5

We know that,
Mode = l + [(f1 - f0) / (2f1 - f0 - f2)] × h
= 25 + [(11 - 9) / (2 × 11 - 9 - 10)] × 5
= 25 + (2 / 3) × 5
= 25 + 3.33
= 28.33

Hence, the correct answer is 28.33.

6. Find the standard deviation of the following data (rounded off to two decimal places).

5, 3, 4, 7

1. 1.48

2. 3.21

3. 4.12

4. 2.45

Correct Answer: A

Standard deviation of 5, 3, 4, 7
= square root of [(sum of squares of the numbers divided by total count) minus (square of the average)]
= √[(5² + 3² + 4² + 7²) / 4 − (5 + 3 + 4 + 7)² / 4²]
= √[(25 + 9 + 16 + 49) / 4 − (19)² / 16]
= √[99 / 4 − 361 / 16]
= √[35 / 16]
= 1.48

Hence, the correct answer is 1.48.

7. A glass jar contains 6 white, 8 black, 4 red, and 3 blue marbles. If a single marble is chosen at random from the jar, what is the probability that it is black or blue?

1. 8/21

2. 11/21

3. 5/21

4. 1/7

Correct Answer: B

Given: A glass jar contains 6 white, 8 black, 4 red, and 3 blue marbles.

Total number of marbles = 6 + 8 + 4 + 3 = 21

Number of black and blue marbles = 8 + 3 = 11

So, the probability of picking a black or blue marble = 11/21

Hence, the correct answer is 11/21.

8. A person can hit a target 5 times out of 8 shots. If he fires 10 shots, what is the probability that he will hit the target twice?

1. (1135 × 3⁸) / 8¹⁰

2. (1165 × 3⁸) / 8¹⁰

3. (1175 × 3⁸) / 8¹⁰

4. (1125 × 3⁸) / 8¹⁰

Correct Answer: D

Solution:

Probability of hitting = 5/8

Probability of losing = 3/8

Probability of hitting twice when 10 shots are fired

= 10C2(5/8)²(3/8)⁸

= (10×9×5×5)/(1×2) × (3⁸)/(8¹⁰)

= 1125 × 3⁸ / 8¹⁰

Hence, the correct answer is 1125 × 3⁸ / 8¹⁰.

9. A speaks the truth 5 out of 7 times and B speaks the truth 8 out of 9 times. What is the probability that they contradict each other in stating the same fact?

1. 1/7

2. 1/9

3. 1/4

4. 1/3

Correct Answer: D

Probability of A speaking truth = 5/7 = P(A)

⇒ Probability of A lying = 1 - 5/7 = 2/7 = P(A')

Probability of B speaking truth = 8/9 = P(B)

⇒ Probability of B lying = 1 - 8/9 = 1/9 = P(B')

Therefore, Required probability

= P(A) × P(B') + P(A') × P(B)

= (5/7) × (1/9) + (2/7) × (8/9)

= 5/63 + 16/63

= 21/63

= 1/3

Hence, the correct answer is 1/3.

TS ICET Statistical Ability Preparation Tips

When compared to the other sections, it can be seen that the statistical ability section of the TS ICET examination is on the easier side. Almost all of the questions asked under this section are easy and straightforward, and not very time-consuming. Some of the effective preparation tips that the candidates can follow under this section are:

• As this section is easier than the other sections of the mathematical ability, it is beneficial for the candidates to start with this section. One of the major advantages is that this may give the candidate confidence while moving ahead, and finishing this section first might also provide them more time for the other questions.

• The statistical ability section is all about formulas. The candidates should memorise all the important formulas in this section and use them whenever required.

• The candidates should begin by learning the basic concepts of statistics such as mean, median, mode, standard deviation, and variance. These form the foundation of the section.

• Once the candidates complete the concepts of mean, median and mode, they should move towards the concept of probability. The candidates must understand simple probability concepts and practice problems related to events, outcomes, and probability formulas.

• After each TS ICET practice test, the candidates must review their errors to avoid repeating them and understand where their concepts need improvement.

TS ICET 2025 Preparation Plan for 2 Months

With two months left for the TS ICET 2025 examination, experts at Careers360 have designed a complete two-month preparation plan for the candidates. According to the TS ICET two-month timetable, a specific set of targets is provided for 8 weeks. Following the timetable can help the candidates complete their TS ICET syllabus well in time, giving them time for solving TS ICET sample papers.

Best Books for TS ICET 2025

With ample time remaining for the TS ICET 2025 exam, this is the ideal moment for candidates to boost their preparation using the best TS ICET 2025 books. Below is a section-wise list of recommended books to help candidates make the most of their final TS ICET preparation phase.