CAT 2025 Quantitative Aptitude Practice Questions with Solutions

CAT 2025 Quantitative Aptitude Practice Questions

The efficiency of the candidate’s CAT Quantitative Aptitude preparation is greatly determined by the number of CAT 2025 Quantitative Aptitude Practice Questions attempted by the candidates. It is important for the candidates to solve a minimum of 50 questions of different types under the CAT QA section to enhance their preparation. A few selected CAT 2025 quantitative aptitude practice questions are listed below for the reference of the candidates.

Arithmetic Section

1. A certain amount of water was poured into a 300-litre container, and the remaining portion of the container was filled with milk. Then an amount of this solution was taken out from the container which was twice the volume of water that was earlier poured into it, and water was poured to refill the container again. If the resulting solution contains 72% milk, then the amount of water, in litres, that was initially poured into the container was

1. 30

2. 40

3. 50

4. 60

Solution:

Let the amount of water initially poured $= x$ litres.

Then, the amount of milk initially $= 300 - x$ litres.

An amount of solution equal to $2x$ litres is removed. This removed solution contains:

Water $= \dfrac{x}{300} \cdot 2x = \dfrac{2x^2}{300}$ litres

Milk $= \dfrac{300-x}{300} \cdot 2x = \dfrac{2x(300-x)}{300}$ litres

Now refill the container with $2x$ litres of water. The final quantities are:

Water $= x - \dfrac{2x^2}{300} + 2x = x\left(1 + 2 - \dfrac{2x}{300}\right) = x\left(3 - \dfrac{2x}{300}\right)$

Milk $= (300 - x) - \dfrac{2x(300-x)}{300} = (300 - x)\left(1 - \dfrac{2x}{300}\right)$

Given: milk is $72%$ of $300$ litres $= 216$ litres

So, $(300 - x)\left(1 - \dfrac{2x}{300}\right) = 216$

$\implies (300 - x)\dfrac{300 - 2x}{300} = 216$

$\implies (300 - x)(300 - 2x) = 216 \cdot 300 = 64800$

$\implies 90000 - 900x + 2x^2 = 64800$

$\implies 2x^2 - 900x + 25200 = 0$

$\implies x^2 - 450x + 12600 = 0$

$\implies x^2 - 420x - 30x + 12600 = 0$

$\implies (x - 420)(x - 30) = 0$

So, $x = 420$ or $x = 30$

Reject $x = 420$ as it exceeds $300$ litres.

Therefore, the amount of water initially poured is $30$ litres.

Hence, the correct answer is $30$.

2. A train travelled a certain distance at a uniform speed. Had the speed been 6 km per hour more, it would have needed 4 hours less. Had the speed been 6 km per hour less, it would have needed 6 hours more. The distance, in km, travelled by the train is

1. 800

2. 720

3. 780

4. 640

Solution:

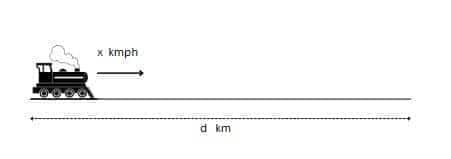
Let the distance be $d$ km and the usual speed be $x$ km/hr. Then, time taken $= \dfrac{d}{x}$.

According to the question:

If speed was increased by $6$ km/hr, time taken would be $4$ hours less:

$\dfrac{d}{x} - \dfrac{d}{x+6} = 4 \quad (1)$

If speed was decreased by $6$ km/hr, time taken would be $6$ hours more:

$\dfrac{d}{x-6} - \dfrac{d}{x} = 6 \quad (2)$

Add equations $(1)$ and $(2)$:

$\left(\dfrac{d}{x} - \dfrac{d}{x+6}\right) + \left(\dfrac{d}{x-6} - \dfrac{d}{x}\right) = 4 + 6$

$\implies \dfrac{d}{x-6} - \dfrac{d}{x+6} = 10$

Take $d$ common:

$d\left(\dfrac{1}{x-6} - \dfrac{1}{x+6}\right) = 10$

$\implies d \cdot \dfrac{(x+6) - (x-6)}{(x-6)(x+6)} = 10$

$\implies d \cdot \dfrac{12}{x^2 - 36} = 10$

$\implies d = \dfrac{10(x^2 - 36)}{12} = \dfrac{5(x^2 - 36)}{6}$

Now, plug this $d$ into equation $(1)$:

$\dfrac{d}{x} - \dfrac{d}{x+6} = 4$

$\implies \dfrac{5(x^2-36)}{6x} - \dfrac{5(x^2-36)}{6(x+6)} = 4$

Take common factor:

$\dfrac{5(x^2-36)}{6} \left(\dfrac{1}{x} - \dfrac{1}{x+6}\right) = 4$

$\implies \dfrac{5(x^2-36)}{6} \cdot \dfrac{6}{x(x+6)} = 4$

$\implies \dfrac{5(x^2-36)}{x(x+6)} = 4$

Simplify:

$5(x^2 - 36) = 4x(x+6)$

$5x^2 - 180 = 4x^2 + 24x$

$x^2 - 24x - 180 = 0$

Solve the quadratic:

$x = \dfrac{24 \pm \sqrt{24^2 + 4 \cdot 180}}{2} = \dfrac{24 \pm \sqrt{576 + 720}}{2} = \dfrac{24 \pm \sqrt{1296}}{2} = \dfrac{24 \pm 36}{2}$

$x = 30$ (discard negative value)

The distance:

$d = \dfrac{5(x^2 - 36)}{6} = \dfrac{5(900 - 36)}{6} = \dfrac{5 \cdot 864}{6} = 720$ km

Hence, the correct answer is option 2.

Time and Work Problem:

3. Renu would take 15 days working 4 hours per day to complete a certain task, whereas Seema would take 8 days working 5 hours per day to complete the same task. They decide to work together to complete this task. Seema agrees to work for double the number of hours per day as Renu, while Renu agrees to work for double the number of days as Seema. If Renu works 2 hours per day, then the number of days Seema will work is

Solution:

Renu would take $15$ days working $4$ hours/day to complete a task, whereas Seema would take $8$ days working $5$ hours/day to complete the same task.

Renu works $2$ hours/day. Let Seema work for $x$ days. Seema agrees to work for double the hours/day as Renu, and Renu agrees to work for double the days as Seema.

Renu's total work = $15 \times 4 = 60$ hours $\implies$ efficiency $= \dfrac{1}{60}$ work per hour.

Seema's total work = $8 \times 5 = 40$ hours $\implies$ efficiency $= \dfrac{1}{40}$ work per hour.

Renu works $2$ hours/day for $2x$ days $\implies$ work done = $2 \cdot 2x \cdot \dfrac{1}{60} = \dfrac{4x}{60} = \dfrac{x}{15}$

Seema works $4$ hours/day (double of Renu) for $x$ days $\implies$ work done = $4 \cdot x \cdot \dfrac{1}{40} = \dfrac{x}{10}$

Total work done = $1$

$\implies \dfrac{x}{15} + \dfrac{x}{10} = 1 \implies \dfrac{2x + 3x}{30} = 1 \implies \dfrac{5x}{30} = 1 \implies x = 6$

Hence, the correct answer is $6$ days.

Algebra Section

1. If $a, b$ and $c$ are positive real numbers such that $a > 10 \ge b \ge c$ and
$\log_8(a+b)\log_2 c + \log_{27}(a-b)\log_3 c = 23$, then the greatest possible integer value of $a$ is

Solution:

$\log_8(a+b)\log_2 c + \log_{27}(a-b)\log_3 c = 23$

$\implies \log_2^3(a+b)\log_2 c + \log_3^3(a-b)\log_3 c = 23$

$\implies \frac{1}{3}\log_2(a+b)\log_2 c + \frac{1}{3}\log_3(a-b)\log_3 c = 23$

$\implies \log_2(a+b)\log_2 c + \log_3(a-b)\log_3 c = 2$

We use change of base formula:

$\log_c(a+b) + \log_c(a-b) = 2$

Use log addition:

$\log_c[(a+b)(a-b)] = 2$

So: $(a+b)(a-b) = c^2 \implies a^2 - b^2 = c^2$

Also, it is given that $a > 10 \ge b \ge c > 0$.

To maximize $a$, $b$ should be minimized, which is $b = 10$ according to the given condition. Now $a$ is maximum if the value of $c$ is close to $10$.

Since $a$ should be an integer satisfying $a^2 = b^2 + c^2$, $b^2 = 100$, $c^2$ is also close to $100$ so as to maximize $a$. The perfect square close to $200$ is $196$.

So, $a^2 = 196 \implies a = 14$.

Hence, the correct answer is 14.

2. If $(a+b\sqrt{3})^2 = 5 + 3\sqrt{3}$, where $a$ and $b$ are natural numbers, then $a+b$ equals

Solution:

We are given: $(a+b\sqrt{3})^2 = 5 + 3\sqrt{3}$

$\implies a^2 + 3b^2 + 2ab\sqrt{3} = 5 + 3\sqrt{3}$

Compare real and irrational parts:

Real part: $a^2 + 3b^2 = 5$

Irrational part: $2ab = 3 \implies ab = \dfrac{3}{2}$

Since $a$ and $b$ are natural numbers, we adjust to match integers: $2ab = 30 \implies ab = 15$

Substitute $b = \dfrac{15}{a}$ into the first equation:

$a^2 + 3\left(\dfrac{15}{a}\right)^2 = 52$

$\implies a^2 + 3 \cdot \dfrac{225}{a^2} = 52$

$\implies a^4 + 675 = 52a^2$

$\implies a^4 - 52a^2 + 675 = 0$

Let $x = a^2$, then: $x^2 - 52x + 675 = 0$

Solve the quadratic equation:

$x = \dfrac{52 \pm \sqrt{52^2 - 4 \cdot 675}}{2} = \dfrac{52 \pm \sqrt{2704 - 2700}}{2} = \dfrac{52 \pm 2}{2}$

$\implies x = 27 \implies a = \sqrt{27}$ (not natural), $x = 25 \implies a = 5$

So $a = 5$, from $ab = 15$, $b = 3$

Therefore: $a+b = 5+3=8$

Hence, the correct answer is option 4.

3. The roots $\alpha, \beta$ of the equation $3x^2 + \lambda x - 1 = 0$ satisfy $\dfrac{1}{\alpha^2} + \dfrac{1}{\beta^2} = 15$. The value of $(\alpha^3 + \beta^3)^2$ is

Solution:

Given: $\dfrac{1}{\alpha^2} + \dfrac{1}{\beta^2} = 15$

We know: $\dfrac{1}{\alpha^2} + \dfrac{1}{\beta^2} = \dfrac{\alpha^2 + \beta^2}{\alpha^2 \beta^2}$

From the equation $3x^2 + \lambda x - 1 = 0$, sum of roots $\alpha + \beta = -\dfrac{\lambda}{3}$, product of roots $\alpha \beta = -\dfrac{1}{3}$

So, $\alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta = \dfrac{\lambda^2}{9} + \dfrac{2}{3}$

Also, $\alpha^2 \beta^2 = (\alpha \beta)^2 = \dfrac{1}{9}$

Now, $\dfrac{\alpha^2 + \beta^2}{\alpha^2 \beta^2} = 15 \implies \dfrac{\frac{\lambda^2}{9} + \frac{2}{3}}{1/9} = 15$

$\implies 9 \left(\frac{\lambda^2}{9} + \frac{2}{3}\right) = 15 \implies \lambda^2 + 6 = 15 \implies \lambda^2 = 9 \implies \lambda = \pm 3$

Now, $\alpha^3 + \beta^3 = (\alpha + \beta)^3 - 3\alpha\beta(\alpha + \beta)$

We have: $\alpha + \beta = -\dfrac{\lambda}{3} = \pm 1$, $\alpha\beta = -\dfrac{1}{3}$

Case 1: $\alpha + \beta = -1$

$\alpha^3 + \beta^3 = (-1)^3 - 3(-1/3)(-1) = -1 -1 = -2$

$(\alpha^3 + \beta^3)^2 = (-2)^2 = 4$

Case 2: $\alpha + \beta = 1$

$\alpha^3 + \beta^3 = 1^3 - 3(-1/3)(1) = 1 + 1 = 2$

$(\alpha^3 + \beta^3)^2 = (2)^2 = 4$

Hence, the correct answer is option 2.

Geometry Section

1. Let C be the circle $x^2+y^2+4x−6y−3=0$ and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to $60 ^\circ$. Then, the point at which L touches the line x=6 is:

1. (6,4)

2. (6,8)

3. (6,3)

4. (6,6)

Solution:

We need to find the equation of a circle at the point of intersection of two tangents (with the same centre).

The general equation of a circle is $x^2 + y^2 + 2gx + 2fy + c = 0$.

The centre of the circle is $(-g, -f)$ and the radius is $\sqrt{g^2 + f^2 - c}$.

For the circle $x^2 + y^2 + 4x - 6y - 3 = 0$, we compare with the general form: $2g = 4 \implies g = 2$ and $2f = -6 \implies f = -3$, and $c = -3$.

So, the centre of the circle is $(-g, -f) = (-2, 3)$.

The radius of the circle is $\sqrt{g^2 + f^2 - c} = \sqrt{2^2 + (-3)^2 - (-3)} = \sqrt{4 + 9 + 3} = \sqrt{16} = 4$.

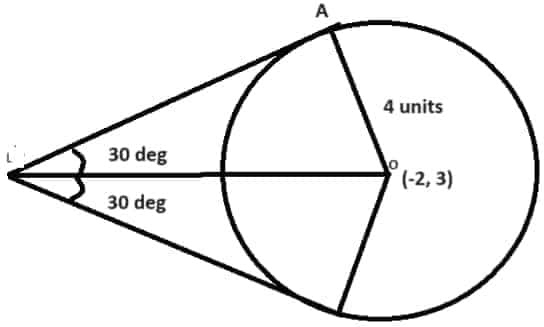
Now, sin⁡30°=4OL

So, OL = 8 units

Equation of circle passing through L: $(x+2)^2+(y−3)^2=8^2$

So, L touches the line x=6 at (6, 3). (put x = 6 in the above equation to get the coordinates).

Hence, the correct answer is option (3).

2. In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP: PQ: QC is

1. 1:1:2

2. 1:2:4

3. 2:4:1

4. 1:2:1

Solution:

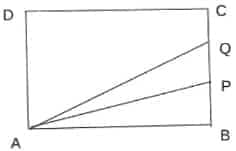
The areas of the figures $ABP$, $APQ$, and $AQCD$ are in geometric progression.

Let Area of $ABP = m$, Area of $APQ = mr$, Area of $AQCD = mr^2$.

Also, Area of $AQCD = 4 \times$ Area of $ABP \implies mr^2 = 4m \implies r = 2$.

The total area of the rectangle $ABCD = 9 \times 6 = 54$.

So, $m + 2m + 4m = 54 \implies 7m = 54 \implies m = \dfrac{54}{7}$.

Area of $ABP = m = \dfrac{54}{7} \implies \dfrac{1}{2} \times AB \times BP = \dfrac{54}{7} \implies BP = \dfrac{12}{7}$ (since $AB = 9$).

Area of $ABQ = 2m + m = 3m = \dfrac{162}{7} \implies \dfrac{1}{2} \times AB \times BQ = \dfrac{162}{7} \implies BQ = \dfrac{36}{7}$ (since $AB = 9$).

Now, $PQ = BQ - BP = \dfrac{36}{7} - \dfrac{12}{7} = \dfrac{24}{7}$.

$QC = BC - BQ = 6 - \dfrac{36}{7} = \dfrac{6}{7}$.

So, $BP : PQ : QC = \dfrac{12}{7} : \dfrac{24}{7} : \dfrac{6}{7} = 2 : 4 : 1$.

Hence, the correct answer is option (3).

3. A triangle is drawn with its vertices on the circle $C$ such that one of its sides is a diameter of $C$ and the other two sides have their lengths in the ratio $a:b$. If the radius of the circle is $r$, then the area of the triangle is:

1. $\dfrac{ab r^2}{2(a^2+b^2)}$

2. $\dfrac{ab r^2}{a^2+b^2}$

3. $\dfrac{4ab r^2}{a^2+b^2}$

4. $\dfrac{2ab r^2}{a^2+b^2}$

Solution:

Let the sides be $ak$ and $bk$. The triangle formed is right-angled because the angle subtended by the diameter of a circle on its circumference is $90^\circ$.

Using Pythagoras theorem: $(2r)^2 = (ak)^2 + (bk)^2 \implies k^2 = \dfrac{4r^2}{a^2+b^2}$

Area of the triangle $= \dfrac{1}{2} \times ak \times bk = \dfrac{1}{2} \times ab k^2 = \dfrac{1}{2} \times ab \times \dfrac{4r^2}{a^2+b^2} = \dfrac{2ab r^2}{a^2+b^2}$

Hence, the correct answer is option (4).

Modern Maths Section

1. The sum of all four-digit numbers that can be formed with the distinct non-zero digits $a, b, c,$ and $d$, with each digit appearing exactly once in every number, is $153310+n$, where $n$ is a single-digit natural number. Then, the value of $(a+b+c+d+n)$ is

Solution:

Total number of 4-digit numbers formed using $a, b, c, d = 4! = 24$. Each digit appears 6 times in each place (units, tens, hundreds, thousands), so the sum of all numbers is $6(a+b+c+d)(1+10+100+1000) = 6(a+b+c+d)\cdot 1111 = 6666(a+b+c+d)$.

Given $6666(a+b+c+d) = 153310 + n$. The sum of $a+b+c+d$ should be so that $6666(a+b+c+d)$ lies between $153310$ and $153320$. Estimate: $\dfrac{153310}{6666} \approx 22.99 \implies a+b+c+d = 23$.

Now, $6666 \times 23 = 153318 \implies n = 153318 - 153310 = 8$. So, $a+b+c+d+n = 23+8=31$.

Hence, the correct answer is 31.

2. In a box of chocolates, there are 4 different types of chocolates. If you want to select 2 chocolates to eat, how many different pairs of chocolates can you choose?

Solution:

To select 2 chocolates from the 4 different types, we use combinations. ${}^4C_2 = \dfrac{4!}{2!(4-2)!} = 6$.

So, you can choose from 6 different pairs of chocolates.

Hence, the correct answer is 6 pairs.

3. How many ways can one choose 6 face cards from a deck of 52 cards such that exactly two kings of the same colour are there?

Solution:

There are only 12 face cards. Let $B_1$ and $B_2$ be two black kings and $R_1$ and $R_2$ be two red kings.

Case 1: $B_1$ and $B_2$ are selected. Then $R_1$ and $R_2$ cannot be selected together. If $R_1$ is selected and $R_2$ is not selected, then the remaining 3 cards must be chosen from 8 cards i.e. ${}^8C_3$ ways. If $R_2$ is selected and $R_1$ is not selected, then the remaining 3 cards must be chosen from the rest of 8 cards i.e. ${}^8C_3$ ways. If $R_1$ and $R_2$ both are not selected, then the remaining 4 cards must be chosen from the rest of 8 cards i.e. ${}^8C_4$ ways. Total ways = ${}^8C_3 + {}^8C_3 + {}^8C_4 = 56 + 56 + 70 = 182$.

Case 2: $R_1$ and $R_2$ are selected. Then $B_1$ and $B_2$ cannot be selected together. If $B_1$ is selected and $B_2$ is not selected, then the remaining 3 cards must be chosen from the rest of 8 cards i.e. ${}^8C_3$ ways. If $B_2$ is selected and $B_1$ is not selected, then the remaining 3 cards must be chosen from the rest of 8 cards i.e. ${}^8C_3$ ways. If $B_1$ and $B_2$ both are not selected, then the remaining 4 cards must be chosen from the rest of 8 cards i.e. ${}^8C_4$ ways. Total ways = ${}^8C_3 + {}^8C_3 + {}^8C_4 = 56 + 56 + 70 = 182$.

So, the answer is $182 + 182 = 364$ ways.

Hence, the correct answer is option (1).

Number Systems Section

1. When $10^{100}$ is divided by $7$, the remainder is

1) 3

2) 4

3) 6

4) 1

Solution:

We know that $10 \div 7$ leaves a remainder of $3$.
So, $10^{100}$ will leave the same remainder as $3^{100}$ when divided by $7$.

Now, $3^3 = 27$ and $27 \div 7$ leaves remainder $-1$ (since $27 = 28 - 1$).

So, $3^{100} = (3^3)^{33} \times 3 = 27^{33} \times 3$
$= (-1)^{33} \times 3 = -3$

Since we want a positive remainder, add $7$:
$-3 + 7 = 4$

The remainder is 4.

Hence, the correct answer is option 2.

2. When $3^{333}$ is divided by $11$, the remainder is

1)5

2) 6

3) 1

4) 10

Solution:

We want the remainder when $3^{333}$ is divided by $11$.

First, observe the powers of $3$ modulo $11$:

• $3^1 \equiv 3 \pmod{11}$

• $3^2 \equiv 9 \pmod{11}$

• $3^3 \equiv 27 \equiv 5 \pmod{11}$

• $3^4 \equiv 15 \equiv 4 \pmod{11}$

• $3^5 \equiv 12 \equiv 1 \pmod{11}$

So, the powers of $3$ repeat every $5$ terms modulo $11$.

Now, divide $333$ by $5$:
$333 \div 5 = 66$ remainder $3$

So, $3^{333} \equiv 3^3 \pmod{11}$
$\implies 3^3 = 27 \equiv 5 \pmod{11}$

We get the remainder as 5.

Hence, the correct answer is option 1.

CAT 2025 Quantitative Aptitude Practice Questions Download Links

As mentioned above, the number of topics that the candidates should prepare under the CAT quantitative aptitude section is very broad and time-consuming. To help the candidates in this regard, Careers360 has performed a comprehensive analysis of the CAT previous year question papers to list the most important CAT quantitative aptitude topics. The candidates must skim through these to find the CAT 2025 Quantitative Aptitude Practice Questions. The most important CAT quantitative aptitude topics, along with the CAT quantitative aptitude sample questions, are provided in the table below.

Quantitative Aptitude Weightage in CAT 2025

• The Quantitative Aptitude section in CAT 2025 carries one-third of the total marks in the CAT Exam 2025, making it equally important as VARC and DILR.

• As per the recent CAT exam pattern 2025, the QA section includes 22 questions out of 66, with +3 marks for each correct answer and -1 negative marking for every wrong attempt.

• Based on previous year analysis, attempting 12 to 14 accurate questions in CAT Quantitative Aptitude is enough to push your score above the 95 percentile range.

• CAT 2025 QA topic-wise weightage is generally distributed as follows:

• 
  

  • Arithmetic – 35% weightage

  • Algebra – 25% weightage

  • Geometry and Mensuration – 20% weightage

  • Numbers and Modern Math – 20% weightage

• Many aspirants score low due to calculation errors and time loss, which makes CAT 2025 Quantitative Aptitude a high-opportunity section for students who prepare with a strategy.

Important Formulas for CAT 2025 Quantitative Aptitude Practice Questions

Mastering the Quantitative Aptitude (QA) section for CAT 2025 requires not just memorising formulas but understanding concepts thoroughly. Practising with CAT 2025 Quantitative Aptitude Practice Questions helps reinforce these concepts, improve speed, and boost accuracy. Key areas to focus on include Arithmetic, Algebra, Geometry, and Modern Math.

Arithmetic

Arithmetic forms the foundation of CAT QA. The formulas are simple, but quick application is crucial. Regular practice with CAT 2025 Quantitative Aptitude Practice Questions will help you solve problems faster and improve accuracy.

Percentages, Profit, and Loss:

Percentage Change $= \dfrac{\text{Final Value} - \text{Initial Value}}{\text{Initial Value}} \times 100$

Profit $= \text{SP} - \text{CP}$;
Profit $% = \dfrac{\text{Profit}}{\text{CP}} \times 100$

Discount $= \text{MP} - \text{SP}$;
Discount $% = \dfrac{\text{Discount}}{\text{MP}} \times 100$

Successive percentage change: an $a%$ increase followed by a $b%$ increase results in a total increase of $\left(a+b+\dfrac{ab}{100}\right)%$.

Time, Speed, and Distance:

Distance $= \text{Speed} \times \text{Time}$

For equal distances with speeds $x$ and $y$:
Average Speed $= \dfrac{2xy}{x+y}$

Relative speed:

• Same direction $= |v_1 - v_2|$

• Opposite direction $= v_1 + v_2$

Time and Work:

If a person can do a work in $n$ days, their one-day work $= \dfrac{1}{n}$

Work $= \text{Efficiency} \times \text{Time}$

Simple and Compound Interest:

Simple Interest (SI): $SI = \dfrac{P \times R \times T}{100}$

Compound Interest (CI): $CI = P\left(1+\dfrac{R}{100}\right)^n - P$

For CI, the amount is $A = P\left(1+\dfrac{R}{100}\right)^n$

Algebra

Algebraic formulas are essential for solving many types of problems, such as quadratic equations, logarithms, and inequalities. Regular practice with CAT 2025 Quantitative Aptitude Practice Questions helps you apply these formulas accurately and quickly.

Basic Algebra & Identities:

$(a+b)^2 = a^2 + 2ab + b^2$

$(a-b)^2 = a^2 - 2ab + b^2$

$a^2 - b^2 = (a+b)(a-b)$

$(a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$

$a^3 + b^3 = (a+b)(a^2 - ab + b^2)$

$a^3 - b^3 = (a-b)(a^2 + ab + b^2)$

If $a+b+c=0$, then $a^3 + b^3 + c^3 = 3abc$

Quadratic Equations:

For $ax^2 + bx + c = 0$, the roots are given by
$x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Sum of roots: $\alpha + \beta = -\dfrac{b}{a}$

Product of roots: $\alpha \beta = \dfrac{c}{a}$

Logarithms:

$\log_b(xy) = \log_b x + \log_b y$

$\log_b!\left(\dfrac{x}{y}\right) = \log_b x - \log_b y$

$\log_b(x^p) = p \log_b x$

Geometry & Mensuration

Geometry questions assess your ability to use geometric principles to calculate areas, perimeters, and volumes of different shapes. Practising with CAT 2025 Quantitative Aptitude Practice Questions strengthens your understanding and improves calculation speed.

2D Shapes:

Triangle: Area $= \tfrac{1}{2} \times \text{base} \times \text{height}$.
Also, Heron’s formula: $\sqrt{s(s-a)(s-b)(s-c)}$, where $s = \tfrac{a+b+c}{2}$.

Circle: Area $= \pi r^2$; Circumference $= 2\pi r$.

Square/Rectangle: Area $= \text{side}^2$ or $l \times b$.
Perimeter $= 4 \times \text{side}$ or $2(l+b)$.

Polygons: Sum of interior angles $= (n-2) \times 180^\circ$.

3D Shapes (Mensuration):

Cube: Volume $= \text{side}^3$; Surface Area $= 6 \times \text{side}^2$.

Cuboid: Volume $= l \times b \times h$; Surface Area $= 2(lb + bh + hl)$.

Cylinder: Volume $= \pi r^2 h$; Total Surface Area $= 2\pi r(r+h)$.

Sphere: Volume $= \tfrac{4}{3}\pi r^3$; Surface Area $= 4\pi r^2$.

Modern Maths

The Modern Math section covers topics like Permutation, Combination, Probability, and Set Theory. While many questions are application-based, knowing a few key formulas is essential. Practising with CAT 2025 Quantitative Aptitude Practice Questions helps you apply these formulas accurately and solve problems more efficiently.

Permutation & Combination:

Permutation: $^nP_r = \dfrac{n!}{(n-r)!}$

Combination: $^nC_r = \dfrac{n!}{r!(n-r)!}$

Probability:

Probability of an event $E$, $P(E) = \dfrac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$

$P(A \cup B) = P(A) + P(B) - P(A \cap B)$

Set Theory:

For two sets $A$ and $B$:
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$

Does Solving CAT 2025 Quantitative Aptitude Practice Questions Guarantee High Percentile

Solving CAT 2025 Quantitative Aptitude practice questions improves problem-solving speed, accuracy, and concept clarity, but it does not guarantee a high percentile alone. Effective preparation requires understanding topic-wise weightage, practising high-frequency questions, and revising formulas and shortcuts.

Topic Preparation Based on Weightage

Students focus on high-frequency areas in Arithmetic, Algebra, Geometry, and Number System according to CAT 2025 topic wise weightage. Practising these topics repeatedly strengthens understanding, helps identify common question patterns, and ensures students concentrate on areas that carry maximum marks in the exam.

Time-Efficient Problem Solving

Solving different types of CAT 2025 Quantitative Aptitude practice questions develops the ability to quickly choose the correct method. Students learn to reduce unnecessary calculations and complete questions faster. This time efficiency is crucial in CAT 2025, where each section has strict time limits.

Error Pattern Analysis

Tracking mistakes in practice questions shows weak areas and recurring errors. Students analyse why they make mistakes and adjust their approach. This improves accuracy and reduces negative marking in CAT 2025 Quantitative Aptitude.

CAT Shortcut & Formula Application

Repeated practice allows students to apply shortcuts, formulas, and approximation methods effectively. Quick application of CAT formulas in arithmetic, algebra, and geometry saves time and increases accuracy, especially in high-weightage questions.

Strategic Attempt Planning

Continuous practice trains students to select questions based on difficulty and marks. They learn to attempt easier, high-scoring questions first and manage time for challenging problems. This strategy maximises scores in CAT 2025 Quantitative Aptitude.

Short Tricks to Solve CAT 2025 Quantitative Aptitude Practice Questions

Short tricks play a vital role in cracking the CAT 2025 Quantitative Aptitude practice questions. They save time, simplify complex calculations, and improve accuracy during the exam. By learning these quick methods, aspirants can approach problems with confidence and solve them faster without relying on lengthy traditional steps.

Break Numbers into Factors

Large numbers can be simplified by breaking them into smaller factors, making calculations faster and more accurate. Practising this trick with CAT 2025 Quantitative Aptitude Practice Questions helps you apply it instinctively during the exam.

Example: Instead of calculating $25 \times 36$ directly, do $25 \times (4 \times 9) = (25 \times 4) \times 9 = 100 \times 9 = 900$.

Use Approximation Smartly

Exact answers aren’t always necessary, especially in comparison-based or estimation questions. Using approximation with CAT 2025 Quantitative Aptitude Practice Questions trains you to get close to the correct answer without lengthy calculations quickly.

Example: If options are far apart, and you need $48%$ of $802$, round to $50%$ of $800 \approx 400$. This quickly gets you close to the answer.

Learn Squares, Cubes, and Tables by Heart

Knowing common squares ($1$–$30$), cubes ($1$–$20$), and multiplication tables saves time and reduces errors. Regular practice with CAT 2025 Quantitative Aptitude Practice Questions reinforces this knowledge for faster calculations.

Example: If you instantly know that $23^2 = 529$, you won’t waste time calculating during the exam.

Apply the Digital Root Method for Checks

The digital root method is a quick way to verify answers in multiplication or addition problems. Applying this technique alongside CAT 2025 Quantitative Aptitude Practice Questions helps reduce careless mistakes.

Example: $236 \to 2+3+6=11 \to 1+1=2$. The answer’s digits should also sum to a multiple of $2$. It’s a quick error-checking trick.

Use the Ratio Method for Percentages

Converting percentages into fractions or ratios speeds up calculations. Practising this method with CAT 2025 Quantitative Aptitude Practice Questions improves accuracy and reduces time spent on repeated calculations.

Example: $20% = \tfrac{1}{5}$, so $20%$ of $250$ is $250/5 = 50$. No calculator, no long steps.

Plug In Options (Back-Solving)

Instead of solving algebraically, testing given options saves time. Practising back-solving with CAT 2025 Quantitative Aptitude Practice Questions helps identify correct answers faster in tricky problems.

Example: If a question asks for a number that gives remainder $3$ when divided by $5$, test the answer options directly. This saves time.

Simplify Before Calculating

Cancelling common terms or simplifying ratios before multiplying reduces calculation steps. Using CAT 2025 Quantitative Aptitude Practice Questions reinforces this habit, making complex calculations quicker and less error-prone.

Example: $\dfrac{24 \times 35}{12 \times 7} = \dfrac{2 \times 35}{7} = 10$. Cutting down numbers first reduces errors and speeds up calculation.

Prioritise Easy Questions First

Attempting simple questions first secures quick marks and builds confidence. Practising this approach with CAT 2025 Quantitative Aptitude Practice Questions helps optimise time management during the exam.

Example: In a set of $10$ QA questions, quickly scan for $4$–$5$ straightforward ones to solve first, securing quick marks and boosting confidence.

CAT 2025 Quantitative Aptitude Previous Year Paper Analysis

Analysing previous CAT Quant papers helps aspirants identify recurring high-weightage topics, difficulty trends, and sectional patterns, which is crucial for planning preparation strategies. Using this analysis alongside the CAT 2025 Quantitative Aptitude Practice Questions can improve accuracy, time management, and confidence.

CAT 2024 Quant Analysis

Overall Difficulty: The CAT 2024 Quant section was generally easy to moderate for most slots, though Slot 3 was slightly tougher with more calculation-heavy questions.

CAT 2024 Slot 1:

• Balanced question distribution with strong focus on Arithmetic and Algebra.

• Geometry was minimally represented, and around 8 TITA (Type In The Answer) questions were included.

• Aspirants who had practised CAT 2025 Quantitative Aptitude Practice Questions for arithmetic topics like Percentages, Profit & Loss, and Simple Interest could attempt these questions quickly with high accuracy.

CAT 2024 Slot 2:

• Key topics included repeated concepts such as Simple & Compound Interest (SICI), Time & Work, and Speed-Time-Distance.

• Arithmetic dominated the section, but some questions required multi-step calculations combining algebra and arithmetic reasoning.

• Regular practice with CAT 2025 Quantitative Aptitude Practice Questions would have helped aspirants manage these multi-step questions efficiently.

CAT 2024 Slot 3:

• Heavily focused on Arithmetic, including SICI, Ratios & Proportions, Time & Work, and Speed-Time-Distance.

• About 10–12 high-confidence attempts could fetch a solid score; aspirants targeting a high percentile needed around 35 marks.

• Practising past CAT 2025 Quantitative Aptitude Practice Questions on these high-weightage topics would have boosted speed and accuracy under exam conditions.

CAT 2023 Quant Analysis

Overall Difficulty: Slightly tougher than CAT 2022, with the overall difficulty ranging from moderate to difficult, depending on the slot.

CAT 2023 Topic Trends:

• Algebra overtook Arithmetic in question count, although Arithmetic remained significant with recurring topics like Speed-Time-Distance, Mixtures, and Alligations.

• Geometry, Modern Math, and Number Theory were included, but their frequency remained moderate.

• Candidates practising CAT 2025 Quantitative Aptitude Practice Questions covering algebraic equations, inequalities, and problem-solving shortcuts would have gained a significant advantage.

CAT 2023 Slot 3:

• Considered the lengthiest and most demanding slot.

• Contained 22 questions: 14 MCQs and 8 TITA questions.

• Many algebra questions were equation-based, requiring multi-step solutions.

• Strong arithmetic foundation and regular practice with CAT 2025 Quantitative Aptitude Practice Questions helped aspirants manage time and maintain accuracy despite the higher difficulty.

CAT 2022 Quant Analysis

Overall Difficulty: Moderate and manageable for most well-prepared candidates, making it slightly easier than subsequent years.

CAT 2022 Topic Distribution:

• Arithmetic remained the most tested area, with high-frequency topics like Time-Speed-Distance, Mixtures, and Alligations.

• Algebra came second in terms of frequency, while Geometry was less emphasised compared to other years.

• Practising CAT 2025 Quantitative Aptitude Practice Questions focusing on these recurring high-weightage topics would have enabled aspirants to secure easy marks quickly.

CAT 2022 Structure & Pattern

• Followed the traditional CAT format with 66 questions overall and a 40-minute sectional time limit.

• CAT 2022 Slot 1 included around 8 TITA questions.

• Aspirants who had trained with a mix of MCQs and TITA-style CAT 2025 Quantitative Aptitude Practice Questions were able to approach both question types confidently and efficiently.

High-Scoring Topics Expected in CAT 2025 Quantitative Aptitude

Focusing on high-scoring topics in CAT Quantitative Aptitude can significantly boost your percentile. These areas often have higher weightage, predictable question patterns, and quicker solving approaches. By mastering topics like arithmetic, algebra, and geometry, aspirants can secure more marks in less time, improving both accuracy and overall performance in the CAT 2025 exam.

Best Resources for CAT Quantitative Aptitude Preparation

Preparing for CAT 2025 Quantitative Aptitude requires the right resources. Using formula sheets, practice sets, sample papers, MCQs, and mock tests helps aspirants improve speed, accuracy, and problem-solving skills. These resources make CAT QA preparation easier and more effective. It also allows candidates to confidently attempt different types of questions in the CAT Exam 2025.

CAT Formula Sheet 2025

A CAT formula sheet contains all the important formulas, shortcuts, and key concepts from different QA topics. Regularly reviewing the CAT 2025 formula sheet helps aspirants recall formulas quickly during practice and exams. It reduces calculation mistakes and saves time, making it one of the most important resources for CAT 2025 Quantitative Aptitude preparation. Using a formula sheet daily strengthens basic concepts and improves problem-solving speed for CAT QA questions.

CAT Practice Set 2025

CAT Practice sets are collections of questions covering all QA topics, including arithmetic, algebra, geometry, and number systems. Solving these sets regularly helps aspirants understand question patterns, improve accuracy, and strengthen weak areas. Practice sets are vital for structured CAT QA preparation, allowing candidates to gradually increase the difficulty level. It also develop confidence in attempting different types of Quantitative Aptitude questions in CAT 2025.

CAT Sample Paper 2025

Sample papers give aspirants an idea of the types and formats of questions asked in the CAT Exam 2025. Practising CAT sample papers helps students get familiar with question difficulty, manage time efficiently, and build accuracy. They are an important part of CAT QA preparation because they provide real exam-like practice and help aspirants analyse their performance before attempting full-length mock tests for CAT 2025.

CAT MCQ

Multiple-choice questions (MCQs) help aspirants practise specific QA concepts quickly and effectively. Solving CAT MCQs improves decision-making, problem-solving speed, and accuracy. MCQs are particularly useful for CAT QA preparation as they cover a wide range of topics and allow aspirants to attempt more questions in less time, boosting confidence and readiness for the CAT 2025 Quantitative Aptitude section.

CAT Mock Test 2025

CAT Mock tests 2025 are full-length practice exams that resemble the actual exam. Taking mock tests helps aspirants check speed, accuracy, and time management. Regular mock tests are essential for CAT QA preparation because they show real exam conditions. It also highlights weak areas and provides insights for improving overall performance in Quantitative Aptitude, helping aspirants achieve a higher percentile in CAT 2025.

Top CAT Quantitative Aptitude Books

If a candidate wishes for more CAT 2025 Quantitative Aptitude Practice Questions, they can refer to the best CAT 2025 preparation books under the CAT quantitative aptitude section. These books are equipped with a variety of CAT quantitative aptitude questions, including the previous year's CAT quant questions and various CAT sample papers and much more, which will enhance the candidate’s CAT preparation and help them stay focused.

CAT Preparation Materials Designed by Careers360

Careers360 designs a set of CAT 2025 preparation resources such as the complete CAT syllabus guides, topic-wise study materials, necessary CAT mock tests, and expert CAT 2025 preparation strategy. Candidates can download these CAT resources using the links provided below.