you just need to get your OBC certificate corrected and need to inform the CAT helpdesk about this error.
Great Lakes - PGDM & PGPM Admissions 2026
Admissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
The CAT Exam Roadmap: Navigating Success through Practice Set Questions- Day 20
Upcoming Event
CAT Admit Card Date:05 Nov' 25 - 30 Nov' 25
Practice sets play a vital role in CAT preparation, offering real-time exam experience and improving accuracy under pressure. On Day 20, Careers360 has curated a dedicated practice test to help candidates get familiar with the actual CAT pattern. Aspirants are encouraged to use this test and continue daily practice using resources in our 60-day CAT preparation strategy. Regular practice with such tests helps tp sharpen problem-solving skills for the CAT 2025 exam.
This Story also Contains
- CAT 2025 Sample Paper with solutions PDF
- CAT 2025 Quantitative Aptitude Sample Papers Solutions
- CAT Logical Reasoning Sample Paper Solutions
- CAT VARC Sample Papers Solutions
- CAT 2025 Ebooks by Careers360
CAT 2025 Sample Paper with solutions PDF
A CAT sample paper with solutions PDF is a mock version of the actual exam, designed to simulate the CAT question pattern and difficulty level. It helps aspirants understand the exam structure, improve time management, and assess their preparation level. Practising sample papers regularly also boosts confidence and highlights weak areas that need focused revision.
This CAT Sample paper consists of three Sections:
Part- A consists of 9 questions.
Part- B consists of 7 questions.
Part- C consists of 9 questions.
Quantitative Aptitude
Q1. For the given pair (x, y) of positive integers, such that (-x + 3y/2) = 7 and x < 210. How many integer values of y satisfy the given conditions? (CAT previous year questions)
340
341
342
1024
CAT 2025: VARC, DILR, and Quant MCQs & Weightages
Comprehensive CAT prep guide with focused practice on Verbal Ability, Data Interpretation & Logical Reasoning, and Quantitative Aptitude.
Download NowQ2. A quadratic function f(x) attains a maximum of 12 at x = 1. The value of the function at x = 0 is 7. What is the value of f (x) at x = -11? (CAT previous year questions)
-805
-719
-859
-883
Q3. If the roots of the equation in y i.e. y3 – ay2 + by – c = 0 are three consecutive integers, then the smallest possible value of b (nearest to its integer value) is ______________ [TITA]
Q4. The sum of the integers in the solution set of |x2 - 7x| > 5 is: (CAT exam model paper)
10
15
20
0
Q5. The equation x2 + ax + (3-b) = 0 has real roots. What is the minimum value of a2 + b2? (CAT previous year questions)
0
2
4
8
Q6. X is p% less than Y and Z is p% more than Y. If X is 2.5p% more than Z, then find p.
(Note: p ≠ 0) - (CAT previous year questions)
20
40
60
50
Q7. The value of the base of a triangle for which area is minimum if the relation between the perpendicular distance from the vertex and the base is p = 7b2 - 84 is _______________ (where b represents base and p represents perpendicular distance) [TITA]
Q8. Let f (x) = max (2x + 1, 3 − 4x), where x is any real number. Value of f(x) at x = 7.5 is: (CAT exam model paper)
-11
- 27
16
43
Q9. Let g (x) be a function such that g (x + 1) g (x) = 12 for every real x. Then what is the value of g (11) g (0)? (CAT exam model paper)
1
12
1/12
6
Logical Reasoning
Direction (Q1-Q3):
Four friends Arun, Bittu, Cirag and Dheeraj went for an excursion with their wives Priya, Renu, Sharita and Varti, not necessarily in the same order. Each couple hails from a different city, including Madurai, Cutnee, Kurnool, and Hapur, but they are not necessarily in that order. They went to Delhi to visit the Pinkfort, where they sat in a row. Each wife always sat to the immediate right of her husband.
(CAT practice questions)
(i) Bittu sat to the immediate right of Priya.
(ii) Dheeraj is from Hapur and Priya is not from Madurai.
(iii) Renu and her husband were sitting to the immediate right of the couple that hailed from Cutnee.
(iv) Chirag and his wife were sitting to the immediate left of the couple from Kurnool and Chirag was sitting to the immediate right of Sharita.
(v) Arun sat to the immediate right of Renu, who is not from Madurai.
Q1. Who is Dheeraj’s wife?
Sharita
Priya
Varti
Renu
Q2. Which couple is from Cutnee?
Varti and Bittu
Dheeraj and Renu
Chirag and Priya
Arun and Sharita
Q3. Who is the husband in the couple, who is seated second in the row from left to right?
Arun
Bittu
Chirag
Dheeraj
Direction (Q4- Q7) (CAT practice questions)
A cube is formed by joining 216 smaller and identical cubes. The bigger cube is painted black colour on all its faces. From the bigger cube, 64 smaller cubes from a corner were taken out and the cube formed by joining these 64 smaller cubes is painted pink in all its faces. Again, this cube is fitted back into its usual position in the large cube.
Q4. How many smaller cubes have no faces painted?
Q5. How many smaller cubes have three faces painted?
Q6. How many smaller cubes have only two faces painted?
Q7. How many smaller cubes have only one face painted?
VARC (CAT solved papers)
In the questions below, find the phrase with an error.
Q1: If I had known, I would lend you my car.
I will lend you my car
I would lent you my car
I would have lent you my car
No improvement needed
Q2. You have no trouble at school, if you had done your homework.
You would have had no trouble at school.
You will have no trouble at school.
You would had no trouble at school
No improvement needed
Q3. If you had done better at your interview, you get that job.
You will get that job.
You would get that job.
You would have got that job.
No improvement needed
Choose appropriate sentence
Q4. While the guests danced, the thieves broke into the house.
While the guests have danced
While the guests were dancing
While the guests had danced
No improvement needed
Error detection - (CAT exam paper sample)
Q5. Take a shower (a)/ you will (b)/ feel better. (c) / No error (d)
(a)
(b)
(c)
(d)
Q6. Whenever I look (a)/ at the moon, my heart (b)/ fills with the pleasure. (c)/ No error(d)
(a)
(b)
(c)
(d)
Q7. The whole block of flats (a)/ including two shops were (b)/ destroyed in fire. (c)/ No error (d)
(a)
(b)
(c)
(d)
Q8. The man who cannot (a)/ believe his senses and the man who cannot (b)/ believe anything else are insane. (c)/ No error(d)
(a)
(b)
(c)
(d)
Fill the blank with the correct Article:
Q9. If you go by __ train you can have quite__ comfortable journey, but make sure you get ___ express, not __ train that stops at all the stations.
a, an, a, the
an, a, the, a
No article, an, a, the
No article, a, an, a
CAT 2025 Quantitative Aptitude Sample Papers Solutions
CAT Quantitative Aptitude sample papers with detailed answers and solutions help in effective preparation. These papers resemble the actual exam pattern and include questions from all three sections, Quantitative Aptitude. Each question is accompanied by a step-by-step solution, helping aspirants understand the correct approach.
Answer 1: (B)
3y/2 = 7 + x
⇒ y = (14 + 2x)/3; for y to be integer (14 + 2x) should be divisible by 3
So, x = 2; y = 6
When x= 5, y = 8
When x = 8, y = 10
When x = 11, y = 12 and so on…
So, there is an AP in x with the first term being 2 and the common difference is 3.
nth term in x must be less than or equal to 210 i.e., 1024.
Therefore, 2 + (n-1)3 ≤ 1024
⇒ n ≤ (1022/3) +1
Therefore, n must be 341.
Hence, there can be 341 solutions.
Answer 2: (D)
If the function gets the maximum of 12 at x = 1
f(x) = a(x – 1)2 + 12
So, f (0) = a + 12 = 7 [Given]
⇒ a = –5
f(x) = –5(x – 1)2 + 12
So, f(-11) = –5(-12 – 1)2 + 12 = –845 + 12 = –833
Hence, the correct answer is –833.
Answer 3:
Let roots be (n - 1), n and (n + 1).
In a cubic equation, the coefficient of y divided by the coefficient of y3 represents the sum of the product of roots taken two at a time.
So, b = the sum of the product of roots taken two at a time
n(n - 1) + (n + 1)n + (n - 1) (n + 1) = b
⇒ n2 - n + n2 + n + n2 - 1 = b
⇒ 3n2 - 1 = b
The value of b will be minimal when the value of n2 is minimum.
i.e., n2 = 0
So, 3 × 0 - 1 = b
∴ b = -1
Hence, the correct answer is -1.
Answer 4: (D)
|x2 - 7x| > 5
⇒ x2 - 7x > 5 or x2 - 7x < -5
Case 1:
⇒ x2-7x > 5
⇒ x2 - 7x – 5 > 0
⇒ x > [(7±√69)/2], which gives two solutions x > 7 or x < 0 (for x to be integer).
Case 2:
⇒ x2 - 7x < -5
⇒ x2 - 7x + 5 < 0
⇒ x < [(7±√29)/2], which gives two solutions x < 7 or x > 0 (for x to be integer).
So, x = [1, 2, 3, 4, 5, 6]
There is no common solution in both cases.
Hence, the correct answer is 0.
Answer 5: (D)
For real roots; a2 – 4(3 – b) ≥ 0
⇒ a2 + 4b – 12 ≥ 0
⇒ a2 + 4b + b2 – b2 – 12 ≥ 0
⇒ a2 + b2 ≥ b2 – 4b + 12
⇒ a2 + b2 ≥ b2 – 4b + 4 + 8
⇒ a2 + b2 ≥ (b – 2)2 + 8
At b = 2, a2 + b2 has the minimum value. i.e., 8.
Hence, the correct answer is 8.
Answer 6: (A)
X = (100 – p) Y/100
Z = (100 + p) Y/100
X = (100 + 2.5p) Z/100
From 1st and 2nd relation, we get X = Z (100 – p) / (100 + p)
So, Z (100 – p) / (100 + p) = (100 + 2.5p) Z/100
⇒ 100(100 – p) = (100 + p) (100 + 2.5p)
⇒ – 100p = 100p – 250p + 2.5p2
⇒ 50p = 2.5p2
⇒ p = 20
Hence, the correct answer is 20.
Answer 7:
Area = ½ (base) (height) = ½ b (7b2 - 84) = 7b3/2 - 84b1/2
For Area to be minimum, find dA/db = 21/2 b2 – 42 = 0
⇒ b2 = 4
⇒ b = 2 or b = -2
Now find d2A/db2 = 21b
At b = 2; d2A/db2 = 42, which is greater than 0.
So, at b = 2, we get the minimum value of Area.
Hence, the correct answer is 2.
Answer 8: (C)
f(x) = max (2 × 7.5 + 1, 3 – 4 × 7.5) at x = 7.5
⇒ f(x) = max (16, -27) at x = 7.5
Hence, the correct answer is 16.
Answer 9: (B)
For x = 0; g(1) = 12/g(0)
Similarly g(2) = 12/g(1), which gives g(2) = g(0)
g(3) = g(1) and so on.
Therefore, g(11) = g(9) = g(7) = ……= g(1) = 12/g(0)
⇒ g (11) g (0) = 12
Hence, the correct answer is 12.
CAT Logical Reasoning Sample Paper Solutions
CAT Logical Reasoning sample paper solutions provide in-depth explanations for a wide range of LR questions, including puzzles, arrangements, blood relations, and logical sequences. These step-by-step solutions help candidates understand the reasoning behind each answer, improve their problem-solving techniques.
Solution 1-3:
Males: Arun, Bittu, Cirag and Dheeraj
Females: Priya, Renu, Sharita and Varti
Cities: Madurai, Cutnee, Kurnool and Hapur
Regarding the couples, the wife always sits to the immediate right of her husband.
From (i), Bittu is not the husband of Priya.
From (ii), Dheeraj is from Hapur.
From (iii), Renu is not from Cutnee.
From (iv), Cirag is not from Kurnool and is not the husband of Sharita.
From (v), Arun is not married to Renu and Renu is not from Madurai.
Possibility Table
HUSBAND | WIFE | CITY |
Bittu | Priya | Hapur |
Dheeraj | Sharita, Reno, Priya, Varita | Hapur |
Chirag | Sharita, Renu, Priya or Varita | Hapur, Kurnool, Mudrai or Cutnee |
Arun | Renu | Hapur, Cutnee, Madurai or Kurnool |
So, according to the table, there were two possibilities for Chirag's wife either Priya or Varita so we will consider these cases one by one.
Case I: If we consider Priya as Chirag’s wife and Priya can’t be from Madurai so they must be from Cutnee.
So, the arrangement could look like this:
------ Sharita Chirag --- Priya Bittu---Renu Arun-------
Now after this arrangement only one man and one woman is left so we can consider the woman as Arun’s wife and the man as Sharita’s Husband
Dheeraj ------ Sharita Chirag --- Priya Bittu---Renu Arun-------Varti
This arrangement fulfils all the conditions, so it is not required to consider any other case.
Answer 1: Dheeraj is married to Sharita. [Which is option (A)]
Answer 2: Chirag and Priya are from Cutnee. [Which is option (C)]
Answer 3: Chirag and his wife are seated second in the row. [Which is option (C)]
Solution 4 to 7:
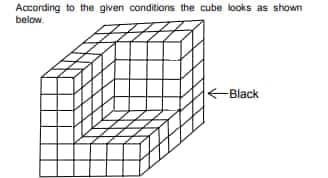
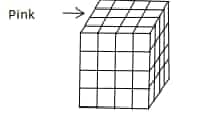
Answer 4: By assuming a 4 × 4 × 4 cube is also not painted with pink colour, the number of cubes with no faces painted is = (6 – 2)3 = 64. Of these 64 smaller cubes now, in the second, third and fourth layers leftmost 9 cubes are painted pink, on the bottom surface four smaller cubes are painted pink and on the fourth layer back six smaller cubes are painted.
Hence, the total number of cubes with no face painted = 64 – 19 = 45
Answer 5: The number of cubes which are three faces painted before removing 64 smaller cubes = 8 and after painting with pink colour to those 64 smaller cubes seven new cubes will have three faces painted.
Hence, the total number of cubes with three faces painted = 8 + 7 = 15
Answer 6: The number of smaller cubes painted on two faces in the larger cube after removing 4 × 4 × 4 is illustrated as shown below.
9 edges with four smaller cubes with two faces painted = 9 × 4 = 36; 3 edges with one cube with two faces painted = 3 × 1 = 3
In the pink cube, there are 24 cubes on 12 edges which are painted on two faces.
Hence, the number of cubes with two faces painted = 36 + 3 + 24 = 63
Answer 7: The number of cubes with one face painted in the larger cube = 3 × 16 + 3 × 7 = 69. Number of cubes with one face painted in the 4 × 4 cube = 6 × 4 = 24
Hence, the total number of smaller cubes with one face painted = 69 + 24 = 93
CAT VARC Sample Papers Solutions
CAT VARC sample paper solutions offer detailed explanations for reading passages, para jumbles, sentence completion, and odd sentence questions. These solutions guide candidates on how to approach each question type, identify key ideas, and eliminate incorrect choices.
Answer 1: (C)
if clause: had known (past perfect), Main clause: would/ could have lent.
Answer 2: (A)
if clause: had done (past perfect), the main clause: would/ could/ might have had.
Answer 3: (C)
if clause: had done (past perfect), the main clause: would/ could/ might have had.
Answer 4: (B)
The previous event is simple past, then the next event must be past continuous for continuous action.
Answer 5: D
“take a shower” is an idiomatic phrase. Hence, No error.
Answer 6: (C)
“with pleasure” is an idiomatic phrase. With pleasure replaced with “pleasure”.
Answer 7: (B)
“was” is used instead of “were”. The whole block is considered a singular subject and the singular subject takes a singular verb.
Answer 8: (D)
when two nouns get added with the use of ‘and’ and a possessive adjective article is used before both nouns then we use a plural verb but when the possessive adjective article is used with only one noun then it is considered to be one and hence singular verb is used.
Answer 9: (D)
No article is used between By and Means of transport.
Before comfortable “a” should be used.
Before “express”, “an” will be used as there is a vowel at the start.
Before “train”, “a” will be used.
CAT 2025 Ebooks by Careers360
CAT 2025 eBooks by Careers360 offer comprehensive preparation material covering Quant, VARC, and DILR. These digital guides include theory, shortcuts, solved examples, and practice questions, helping aspirants strengthen concepts and enhance exam strategy for a high percentile score.
eBook Title | Download Links |
3000+ Most Important Words - Vocabulary Builder | |
500+ Most Important Idioms and Phrases | |
300+ Most Important Phrasal Verbs | |
CAT 2025 Verbal Ability and Reading Comprehension (VARC) Study Material | |
Permutation & Combination - Video Lectures and Practice Questions | |
Mastering DILR Questions with Expert Solutions | |
CAT 2025 Exam's High Scoring Chapters and Topics | |
Mastering CAT Exam: VARC, DILR, and Quant MCQs & Weightages | |
CAT 2025 Mastery: Chapter-wise MCQs for Success for VARC, DILR, Quant | |
CAT 2025 Quantitative Aptitude Questions with Answers | |
CAT DILR Questions with Solution, Download LRDI Questions for CAT |
Frequently Asked Questions (FAQs)
Q: How can I use CAT 2025 practice sets to improve my weak areas?
A:
Identify topics where you make mistakes while solving practice sets. Spend extra time revising those concepts and solving more questions from those areas.
Q: Can practice sets replace mock tests in CAT preparation?
A:
Practice sets are great for focused learning, but cannot replace mock tests. Mock tests simulate the real exam environment and test your overall readiness.
Q: Why are practice set questions important in CAT preparation?
A:
Practice sets help you apply concepts and improve problem-solving speed. They prepare you for different question types and build exam confidence.
Q: How often should I attempt CAT practice sets during my preparation?
A:
You should attempt practice sets regularly to stay consistent. Daily or alternate-day practice helps track progress effectively.
Q: What should I do after completing a CAT practice set?
A:
Always review your answers carefully. Understand your mistakes and learn the correct approach. This helps avoid repeating errors in future tests.
Q: Do these practice tests help me to score well?
A:
Yes absolutely, practices will make you better, helping in increase of speed and accuracy.
Q: What are real roots?
A:
Real roots are real-valued equation solutions. This implies that they may be positive, negative, or zero, but not imaginary or complex. The real roots of the equation x^2-4=0 are x=2 and x=-2, which are both real values that satisfy the equation. Simply said, real roots are the values of a variable that satisfy the equation and may be found on the number line.
Q: How many roots can a quadratic equation have?
A:
There can be 1, 0, or 2 roots in a quadratic equation.
Q: What are the roots of a quadratic equation?
A:
The roots are the values of 'x' for which the quadratic equation is true, indicating where the graph intersects the x-axis.
Q: What is a quadratic function?
A:
A quadratic function is a degree two polynomial function in which the variable's maximum exponent is 2.
Articles
Related Stories
|
Upcoming Bschool Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Popular Courses and Specializations
List of colleges accepting CAT
Browse Bschool Colleges by State
Questions related to CAT
On Question asked by student community
Have a question related to CAT ?
The three key formulas that can solve almost all Profit & Loss problems are:
-
Profit/Loss % = (Profit or Loss / Cost Price) × 100%, where CP is the cost price.
-
Discount % = (Discount / Marked Price) × 100%, where MP is the marked price.
-
Mark up % = (Mark up Value / Cost Price) × 100%, where CP is the cost price.
These formulas can be adapted for problems involving discounts, marked price, or successive gains/losses.
For detailed examples and variations, you can from the article
With a 70 percent in CAT Examination, you can go for various B-Schools or private collages. The S. K. Patel Institute of Management in Gandhinagar is an option for those who score 70-80 percent in their CAT examination or The Gujarat Institute of Management (GIM) in Goa with a cutoff of 60-80 percentage. These are the collages you can look for in Gujarat or nearby.
Collage in other regions: BA Colleges Accepting 70-80 Percentile in CAT 2025
Thank You.
Hello dear candidate,
NO. your application for CAT will not rejected for wrong gender small mistake in the OBC NCL certificate. You will be considered as an OBC candidate.
Hello,
Here are some top MBA colleges in India with fees under Rs. 2 lakh and their exam/cutoff details:
-
SIMSREE, Mumbai – Fee around Rs. 1.3–1.4 lakh for 2 years. Accepts CAT, CMAT, MAH-CET, MAT, ATMA. Cutoff is very high, usually 99+ percentile in CAT/CMAT.
-
PUMBA (Dept. of Management Sciences, Savitribai Phule Pune University) – Fee around Rs. 1.2–1.3 lakh. Accepts CAT, CMAT, MAH-CET, ATMA. Cutoff approx. 75+ percentile in CAT, 90–95+ percentile in CMAT, high scores in MAH-CET.
-
TISS, Mumbai (MA HRM & other management-related programmes) – Fee around Rs. 1.7–1.9 lakh. Accepts CAT for some courses. Qualifying cutoff is around 60–70 percentile, but final selection cutoffs are higher.
These are the main government institutes where the full MBA/PG programme fee is within Rs. 2 lakh. Cutoffs vary slightly each year and by category, but SIMSREE and PUMBA generally need high scores, while TISS has its own process along with CAT shortlisting.
Hope it helps !
Hey! With a NEET score of 344 in the ST category, it is highly unlikely to get admission in any government BDS college in Delhi through the All India Quota. The cutoff for government BDS seats in Delhi usually falls around 400–450 for ST category, so your score is below that range.
You can consider private dental colleges, state quota seats in other states, or reattempt NEET next year to improve your chances.
Popular CAT Questions
Directions for question :
M/s Deloitte Touche Tohmatsu Limited, one of the top four audit and accounting firms in the world with headquarters at London, UK, and with an operational presence in 153 countries, hires Management Trainees (MT) from all the premier management institutes of India thrice every year, in the months of January, May and September.
Each new group of Management Trainees (MT) have to go through a four month rigorous training schedule, after which they have to pass through a test consisting of a written assessment and a case-analysis. The top hundred ranked Management Trainees (MT) based on the performance in the test are confirmed as Management Executives (ME). The rest are given the opportunity of undergoing the training for four months one more time along with the next batch of Management Trainees (MT) and then passing through the subsequent test consisting of the written assessment and case-analysis. The Management Trainee (MT) who fails to get confirmed as a Management Executive (ME) the second time is fired.
The scatter-graph below depicts the number of Management Trainees (MT) at Deloitte taking the tests from January 2020 till May 2022, and the vis-à-vis hired Management Trainees (MT) at Deloitte who were fired :
It is also known that for the month of September 2019 at Deloitte, 96 hired Management Trainees (MT) failed to be confirmed as a Management Executive (ME) the first time, and that 36 hired Management Trainees (MT) were fired.
Question :
In which test did the minimum number of Management Trainees (MT) get confirmed as a Management Executive (ME) in the second attempt ?
Option: 1
September 2020
Option: 2
May 2021
Option: 3
January 2021
Option: 4
January 2022
Directions for question:
The bar-graph given below shows the foreign exchange reserves of Nepal (in million Rupees) from 2014 to 2021. Answer the following questions based on the graph :
Question:
What was the percentage increase (rounded to the nearest integer, if deemed necessary) in the foreign exchange reserves in 2020 over 2016 ?
Option: 1 None
Option: 2 None
Option: 3 None
Option: 4 None
MBA/PGDM Admissions OPEN
Great Lakes Institute of Management PGPM Admissions 2026
ApplyAdmissions Open | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025
IMT Ghaziabad PGDM Admissions 2026
ApplyAACSB, NBA & SAQS Accredited | H-CTC 41.55 LPA | Merit Based Scholarship
SPJIMR Mumbai PGDM Admissions 2026
ApplyRanked No. 3 Business School in India and no.35 in world by Financial Times MiM 2025 Ranking | Highest CTC: INR 89 LPA
Symbiosis MBA - SNAP 2025
Apply1 Exam accepted by 17 Top Symbiosis Institutes for 29 MBA programmes.
IBSAT 2025-ICFAI Business School MBA/PGPM 2026
ApplyIBSAT 2025-Your gateway to MBA/PGPM @ IBS Hyderabad and 8 other IBS campuses | Scholarships worth 10 CR
FLAME University | MBA 2026
ApplyNAAC A++ Grade | MBA program graded A** (National) by CRISIL | AACSB, ACBSP and BGA Member
CAT Notifications
Never miss an CAT update
Get timely CAT updates directly to your inbox. Stay informed!