AP ICET 2025 Mathematical Ability: Important Topics, Sample Questions & Paper Pattern

AP ICET 2025 Mathematical Ability: Section C of the AP ICET 2025 question paper is the Mathematical Ability section. 55 questions are asked under this section. With less than a month left for the AP ICET 2025 exam, the candidates must brush up on their AP ICET Mathematics concepts during this period. Generally, solving the Mathematical questions may require more time when compared to the other sections. Due to this, the candidates must use time management skills to ensure that they complete answering as many questions as possible within the stipulated time. Due to the moderate to difficult nature of the Mathematical Ability section of the AP ICET exam’s Mathematical Ability section, it is often considered to be decisive for the candidate’s selection to their dream colleges using the AP ICET score. This article of Careers360 includes various AP ICET Mathematical Ability model questions. These AP ICET Mathematical Ability sample questions let the candidate know about the types and difficulty level of the Mathematical ability section of the AP ICET 2025 examination. By solving these AP ICET Mathematical Ability sample questions, the candidates will get an understanding of what to expect during the AP ICET 2025 examination.

New: AP ICET: Business and Computer Terminology

Don't Miss: APICET Mock Test: Detailed Solutions

Also See: AP ICET 2025 Sample Papers with Solutions

Admission Alert: MBA @ GITAM School of Business

This Story also Contains

1. AP ICET 2025 Exam Pattern
2. AP ICET 2025 Mathematical Ability Overview
3. AP ICET Mathematical Ability Sample Questions: Arithmetical Ability
4. AP ICET Mathematical Ability Sample Questions: Algebraical and Geometrical Ability
5. AP ICET Mathematical Ability Sample Questions: Statistical Ability
6. AP ICET 2025 Preparation Books
7. AP ICET 2025 Practice Resources by Careers360

AP ICET 2025 Exam Pattern

The AP ICET exam 2025 will be following the same pattern of the previous years, as there is no official update from the exam-conducting bodies related to any changes in the pattern. The AP ICET 2025 exam pattern, as well as the syllabus, will remain the same as the previous years. The overview of the AP ICET exam pattern is given below.

AP ICET 2025 Mathematical Ability Overview

The last section of the AP ICET 2025 question paper will be the Mathematical ability section with 55 questions. It is broadly divided into three sections: arithmetic ability section, algebraic section and the statistical ability section, with arithmetic being the dominant section with 35 questions. The overall question distribution of the Mathematical ability of the AP ICET 2025 exam is given below:

AP ICET Mathematical Ability Sample Questions: Arithmetical Ability

The arithmetical ability questions of the AP ICET examination hold 63% of the weightage in the mathematical ability section of the AP ICET 2025 question paper. Hence, while preparing for the mathematical ability section of the AP ICET 2025 examination, the candidates should prioritise this section. The concepts from which the questions are asked from the mathematical ability of the AP ICET exam includes, mensuration, profit and loss, time and work, problems on train, ratio and proportion, problems on ages, pipes and cisterns, matrices, surds and indices, probability, Arithmetic and Geometric Progressions, trigonometry, height and distance, quadratic equations, LCM and HCF, Interests, partnerships and so on. Since the questions can be asked from wide range of topics, it is necessary for the candidates to

1. A person lent a certain sum of money at the annual rate of 7% on simple interest and the interest received in 11 years is Rs. 920 less than the sum lent. What is the sum lent?

1. Rs. 41200

2. Rs. 4000

3. Rs. 52000

4. Rs. 2400

Correct Answer: Option B

Given, Rate = 7% and Time = 11 years

Let the amount lent be P

Interest earned = P - 920

According to the formula, Simple interest = (P × R × T) / 100, where P, R, and T are the principal, rate of interest, and time.

Therefore, P - 920 = (P × 7 × 11) / 100

Simplifying, 100P - 92000 = 77P

So, 100P - 77P = 92000

This implies 23P = 92000

Therefore, P = 4000

Hence, the correct answer is Rs. 4000.

2. The volume of the sphere is 38,808 cm3. What is the surface area of the sphere?

1. 4455 cm2

2. 4433 cm2

3. 5544.cm2

4. 3344 cm2

Correct Answer: Option C

Given, volume of the sphere = 38,808 cm³

Volume of the sphere = (4/3) * π * r³

(4/3) * π * r³ = 38,808

r³ = (38808 * 3 * 7) / (4 * 22) = 9261

r = 21

Surface area of the sphere = 4 * π * r²

= 4 * (22/7) * 21²

= 5544 cm²

Hence, the answer is 5544 cm².

3. The printed price of a TV set is INR 14,500. It is sold for INR 10,000 with two consecutive discounts. If the first discount is 10%, then what is the second discount?

1. 23.37%

2. 25.37%

3. 20.37%

4. 27.37%

Correct Answer: Option A

Marked price of TV = INR 14,500

Selling price of TV = INR 10,000

First discount percentage = 10%

Let the second discount percentage be b%.

Total discount given = (14500 - 10000) / 14500 × 100 = 31.034%

We know the final discount after two consecutive discounts of a% and b% = (a + b - a × b / 100)%

So, 31.034 = (10 + b - 10 × b / 100)%

This implies 21.034 = b - 0.1b

Therefore, b = 21.034 / 0.9

So, b = 23.37%

Hence, the answer is 23.37%.

4. From point H, at 6:30 pm, a train starts moving towards point K at the speed of 90 km/hr. Another train starts moving from point K at 7:30 p.m. towards point H at the speed of 72 km/hr. Both trains meet at 11:30 p.m. at point J. What is the ratio of the distance HJ and KJ?

1. 25 : 16

2. 5 : 16

3. 36 : 25

4. 31 : 19

Correct Answer: Option A

Given, H to K = 6:30 pm at 90 km/h

K to H = 7:30 pm at 72 km/h

J = 11:30 pm

The time between 6:30 pm and 11:30 pm = 5 hours

Therefore, Distance between point H and J = 90 × 5 = 450 km

The time between 7:30 pm and 11:30 pm = 4 hours

Therefore, Distance between points K and J = 72 × 4 = 288 km

So, the Ratio of Distance HJ & KJ = 450 : 288 = 25 : 16

Hence, the correct answer is 25 : 16.

5. A and B working separately can complete a piece of work in 10 and 16 days, respectively. If they work for a day alternately, with A beginning the work, in how many day(s) will the work be completed?

1. 10 1/4

2. 12 1/4

3. 1 1/4

4. 1/4

Correct Answer: Option B

Let the total work be 80 units.

The efficiency of A and B is 8 units/day and 5 units/day, respectively.

The effective efficiency of A and B working alternately is 13 units/day.

In 12 days, the work completed is 78 units.

The remaining 2 units will be completed by A in 1/4 day.

Therefore, the total time is 12 1/4 days.

6. Prasad goes 96 kilometres on a bike at a speed of 16 km/h, 124 kilometres at 31 km/h in a car, and 105 kilometres at 7 km/h in a horse cart. Find his average speed for the entire distance travelled.

1. 16 km/h

2. 13 km/h

3. 17 km/h

4. 11 km/h

Correct Answer: Option B

Prasad goes 96 kilometres on a bike at a speed of 16 km/h, 124 kilometres at 31 km/h in a car, and 105 kilometres at 7 km/h in a horsecart.

Total distance travelled = 96 + 124 + 105 = 325 km

Total time taken = (96 / 16) + (124 / 31) + (105 / 7) = 6 + 4 + 15 = 25 hours

Average speed = Total distance / Total time taken = 325 / 25 = 13 km/h

Hence, the required average speed is 13 km/h.

7. A and B can do a certain work in 6 hours, and A, B and C together take 4 hours to do the same. How long will it take for C alone to accomplish the task?

1. 12 hours

2. 4 hours

3. 2 hours

4. 6 hours

Correct Answer: Option A

1-hour task of (A + B) = 1/6

1-hour task of (A + B + C) = 1/4

Task done by C alone = 1/4 - 1/6

(6 - 4) / 24

2 / 24

1 / 12

Done by C alone = 12 hours

Hence, the correct answer is 12 hours.

8. If the HCF of two numbers is 8, then which of the following can NEVER be their LCM?

1. 56

2. 48

3. 42

4. 40

Correct Answer: Option C

Since the HCF of two numbers is 8,

LCM will only be multiples of 8.

So LCM can be 56, 48, and 40 and never be 42.

Hence the answer is 42.

9. What is the smallest perfect square which is completely divisible by each of 16, 18 and 36?

1. 144

2. 81

3. 196

4. 169

Correct Answer: Option B

Smallest number divisible by 16, 18 and 36 = LCM(16, 18, 36) = 144

144 is a perfect square itself.

Hence, the answer is 144.

10. Find the greatest number that will divide 49, 147, and 322 to leave the same remainder in each case.

1. 9

2. 5

3. 7

4. 8

Correct Answer: Option C

According to the question,

The differences will be,

⇒ 147 – 49 = 98

⇒ 322 – 147 = 175

⇒ 322 – 49 = 273

The set of numbers {98,175,273}

Now HCF of {98,175,273}

⇒ 98 = 7 × 7 × 2

⇒ 175 = 5 × 5 × 7

⇒ 273 = 13 × 7 × 3

The HCF of {98,175,273} is 7

The same remainder in each case is 7.

11. 5 men and 8 women can complete a work in 12 days working together, while 3 men and 7 women together can complete the same work in 15 days. In how many days will 11 women complete the same work?

1. 12

2. 8

3. 6

4. 16

Correct Answer: Option A

Given, 5 men and 8 women can complete a work in 12 days working together.

3 men and 7 women together can complete the same work in 15 days.

Let the work done by a man and a woman in a day be a and b units.

According to the question, 5(12)a + 8(12)b = 3(15)a + 7(15)b.

This simplifies to 15a = 9b.

So, a = 3/5b.

Also, 5(12)a + 8(12)b = 1.

This simplifies to 132b = 1.

So, b = 1/132.

Work done by 11 women in a day = 11 × 1/132 = 1/12.

Hence, the time taken by 11 women to complete the work is 12 days.

12. In a linear race of 1000 m, A beats B by 50 m or 5 seconds. What is the difference between the speeds (in m/s) of A and B?

1. 1 10/19

2. 10/19

3. 9/19

4. 9/10

Correct Answer: Option B

Given that in a linear race of 1000 m, A beats B by 50 m or 5 seconds.

When A covers 1000 m, B covers 950 m

Also, B covers 50 m in 5 sec

The speed of B = 50 / 5 = 10 m/sec

To cover 950 m, B will take 950 / 10 = 95 sec

As the time of covering 1000 m by A is the same as covering 950 m by B

So, the speed of A = 1000 / 95 = 200 / 19 m/sec

Difference = 200 / 19 – 10 = (200 – 190) / 19 = 10 / 19 m/sec

Hence, the correct answer is 10 / 19.

13. Vikas covered a certain distance by bike. If he covers 40% of the distance at 40 km/h, 50% of the distance at 25 km/h and the remaining 10% distance at 10 km/h. Find his average speed over the whole distance.

1. 25 km/h

2. 28 km/h

3. 26 km/h

4. 30 km/h

Correct Answer: Option A

Let the total distance be 100x.

Vikas covers:

40% of the distance at 40 km/h,

50% of the distance at 25 km/h,

The remaining 10% distance at 10 km/h.

We can calculate the average speed using the formula:

Average speed = Total distance / Total time

The total time taken can be calculated by summing up the time taken for each segment of the distance:

Total time = Distance / Speed

So, the average speed is given by:

Average speed = 100x / (40/40 + 50/25 + 10/10)

Simplifying,

Average speed = 100x / (1 + 2 + 1) = 100x / 4x = 25 km/h

Hence, the correct answer is 25 km/h.

14. A shopkeeper listed the marked price of a chair at a certain amount. If the shopkeeper declares a 15% discount and sells it at Rs.1,445, then what is the marked price?

1. Rs. 1,750

2. Rs. 1,800

3. Rs. 1,700

4. Rs. 1,850

Correct Answer: Option C

Selling price = Rs.1445

Discount = 15% of marked price

Selling price = Marked price – discount

85% of marked price = 1445

Marked price = (144500 / 85) = Rs.1700

Hence, the answer is Rs.1700.

15. If the price of petrol increased by 7%, then by what percentage should the consumption be decreased by the consumer, if the expenditure on petrol remains unchanged?

1. 6 58/107%

2. 5 11/107%

3. 3 49/107%

4. 4 99/107%

Correct Answer: Option B

Let the price of petrol be Rs. 100.

The price of petrol increases by 7%, the new price = 100 + 7% of 100 = 107

The price of petrol increases by 7%, the new price = INR 107

The consumption will be decreased by the consumer if the expenditure on petrol remains unchanged.

Required percentage = (107 - 100) / 107 × 100 = 700 / 107%

Therefore, the correct answer is 6 58/107%.

AP ICET Arithmetic Ability Preparation Tips

Given below are a few AP ICET preparation tips for Mathematical Ability that can be followed by the candidates to perform well in this section of the AP ICET examination.

• Studying mathematical concepts depends heavily on understanding the basics of concepts. Conceptual knowledge must be given priority over mugging up. The candidates should solve a lot of questions and understand the concepts by building a clear understanding of fundamental concepts in arithmetic, algebra, geometry, and statistics.

• Practicing for the mathematics section involves the investment of a lot of practice and time. The candidates must practice regularly and, if possible, create a timetable by dividing each concept into time slots for learning the concepts well.

• Memorizing the formulas is key to success in the arithmetic ability section of the AP ICET exam. The candidates should also study shortcut methods to solve the questions fast, and it must also be applied while they practice various AP ICET mathematical ability sample questions as well.

• The candidates should also put efforts into solving the various AP ICET previous year question papers. This would enable the candidates to understand the difficulty level of the examination and give them enough AP ICET mathematical ability practice along with the AP ICET mathematical ability sample questions.

• Along with solving the AP ICET mathematical ability model questions and sample questions, the candidates should also solve various AP ICET mock tests and sample papers to strengthen their AP ICET preparation.

AP ICET Mathematical Ability Sample Questions: Algebraical and Geometrical Ability

Under the algebraical and geometry ability topic of the Mathematical Ability section of the AP ICET exam, the candidates are tested on topics such as lines and angles, height and distance, trigonometric functions and so on. 10 questions will be asked from this section. The candidates are advised to practice this section with more attention to detail because while analysing the past papers, it was observed that the questions asked under the Algebraical and Geometrical Ability section were a bit more time-consuming to solve and challenging. Given below are a few selected AP ICET mathematical ability sample questions on both the algebraical and geometrical ability section for the practice of the candidates.

1. The angle of elevation of the top of a tower 25√3 m high from two points on the level ground on its opposite sides are 45° and 60°. What is the distance (in m) between the two points (correct to one decimal place)?

1. 45.3

2. 58.4

3. 68.3

4. 50.6

Solution:

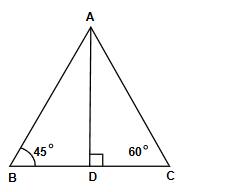
Let the distances from the two points on the ground to the base of the tower be d₁ and d₂.
The angles of elevation from these points to the top of the tower are 45° and 60°, respectively.

In triangle ABD,
tan(45°) = AD / BD
⇒ 1 = 25√3 / d₁
⇒ d₁ = 25√3 = 25 × 1.732 = 43.3 m

In triangle ADC,
tan(60°) = AD / DC
⇒ √3 = 25√3 / d₂
⇒ d₂ = 25 m

Therefore, the distance between the two points = d₁ + d₂ = 43.3 + 25 = 68.3 m
Hence, the correct answer is 68.3 m.

2. A person 1.8 metres tall is 30√3 metres away from a tower. If the angle of elevation from his eye to the top of the tower is 30 degrees, then what is the height (in metres) of the tower?

1. 32.5

2. 37.8

3. 30.5

4. 31.8

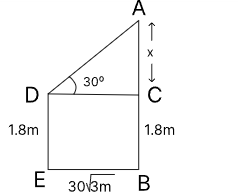
Given: A person 1.8 metres tall is 30√3 metres away from a tower.
The angle of elevation from his eye to the top of the tower is 30 degrees.
We know the formulas: tan 30° = 1/√3 and tan θ = Perpendicular / Base.
Let the tower's height and the person's height be AB and DE, respectively.

In triangle ACD,
AC / DC = tan 30°
⇒ x / (30√3) = 1 / √3
⇒ x = 30 metres

The height of the tower AB = 30 + 1.8 = 31.8 metres
Hence, the correct answer is 31.8 metres.

3. If cosec θ = b ÷ a, then (√3 × cot θ + 1) ÷ (tan θ + √3) = ?

1. √(b² − a²) ÷ b

2. √(b² − a²) ÷ a

3. √(a² + b²) ÷ a

4. √(a² + b²) ÷ b

Given,
cosec(θ) = b / a
⇒ sin(θ) = a / b

We have to find the value of (√3 * cot(θ) + 1) / (tan(θ) + √3)

We know, cot(θ) = cos(θ) / sin(θ) and tan(θ) = sin(θ) / cos(θ)

(√3 * cot(θ) + 1) / (tan(θ) + √3) = (√3 * (cos(θ) / sin(θ)) + 1) / (sin(θ) / cos(θ) + √3)

= (cos(θ) * (√3 * cos(θ) + sin(θ))) / (sin(θ) * (sin(θ) + √3 * cos(θ)))

= cos(θ) / sin(θ)

= √(1 - sin²(θ)) / sin(θ) [As sin²(θ) + cos²(θ) = 1]

= √(1 - (a / b)²) / (a / b)

= √(b² - a²) / a

Hence, the correct answer is √(b² - a²) / a.

3. If √3 tan(θ) = 3 sin(θ), then what is the value of sin²(θ) - cos²(θ)?

1. 1/5

2. 1/4

3. 1/2

4. 1/3

Given:
√3 tan(θ) = 3 * sin(θ)
⇒ √3 * (sin(θ) / cos(θ)) = 3 * sin(θ)
⇒ √3 / 3 = cos(θ)
⇒ cos(θ) = 1 / √3

Squaring both sides:
cos²(θ) = 1 / 3 (Equation 1)

Using the trigonometric identity:
sin²(θ) + cos²(θ) = 1
Substitute cos²(θ) from Equation 1:
sin²(θ) + 1/3 = 1
⇒ sin²(θ) = 1 - 1/3
⇒ sin²(θ) = 2/3

The value of sin²(θ) - cos²(θ) = 2/3 - 1/3 = 1/3.

Hence, the correct answer is 1/3.

4. The interior angle of a regular polygon exceeds its exterior angle by 90°. The number of sides of the polygon is:

1. 8

2. 6

3. 10

4. 12

Given: The interior angle of a regular polygon exceeds its exterior angle by 90°.
Let x be the polygon's exterior angle and n be its number of sides.
A regular polygon's sum of its exterior and interior angles is 180°.
A regular polygon's exterior angle is 360° / n, where n is the number of sides.

According to the question,
x + x + 90° = 180°
⇒ 2x = 90°
⇒ x = 45°

The number of sides of the polygon is given as,
45° = 360° / n
⇒ n = 8

Hence, the correct answer is 8.

5. ABC is an isosceles triangle having AB = AC and ∠A = 40°. Bisector PO and OQ of the exterior angle ∠ABD and ∠ACE formed by producing BC on both sides, meet at O, then the value of ∠BOC is:

1. 70°

2. 110°

3. 80°

4. 55°

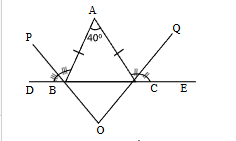
Given, an isosceles triangle ABC with AB = AC and ∠A = 40°. Bisectors PO and OQ of ∠ABD and ∠ACE.

In triangle ABC, ∠A + ∠B + ∠C = 180°. Or, 40° + 2∠C = 180°. Or, ∠B = ∠C = 70°.

Now, ∠ABD + ∠ABC = 180°. Or, ∠ABD + 70° = 180°. Or, ∠ABD = 110°.

Since PO is an angle bisector, ∠PBD = 110° / 2 = 55°. Similarly, ∠QCE = 55°.

In triangle BCO, ∠BOC + ∠CBO + ∠BCO = 180°. Or, ∠BOC + ∠PBD + ∠QCE = 180° (vertically opposite angles). Or, ∠BOC + 55° + 55° = 180°. Or, ∠BOC = 70°.

Hence, the correct answer is 70°.

6. Find the equation of the line perpendicular to x - 2y + 3 = 0 and passing through (1, 0).

1. 2x + y - 2 = 0

2. x + 2y - 2 = 0

3. 2x + y + 2 = 0

4. x + 2y + 2 = 0

Line perpendicular to x - 2y + 3 = 0 is:

2x + y + λ = 0

Now it passes through the point (1, 0).

So,
2 × 1 + 0 + λ = 0
⇒ λ = -2

Hence, the answer is option 1.

AP ICET Algebraical and Geometrical Ability Preparation Tips

Preparing for the algebraical and geometrical ability section of the AP ICET exam might be difficult due to the presence of the variety of questions asked of varying difficulty. To strategise their preparation, the candidates can follow the tips given below.

• If a candidate finds it overwhelming to study a concept, they can break down the concepts into smaller chunks and study them. Although this may take slightly longer for understanding the concepts, it can help the candidates to attain conceptual clarity, which is crucial for solving both the Algebraical and Geometrical ability questions in the examination.

• If the candidates find the concepts of geometry difficult to understand, they can compare them with real-life structures to understand better.

• Maintain a separate sheet with key algebra and geometry formulas for quick revision.

• There will be concepts of a slightly more advanced level in each topic of the Algebraical and Geometrical sections. The candidates should not overlook these concepts and instead try their best to understand and solve them. Completely ignoring a concept could be fatal in an exam.

• The candidates must identify topics where they struggle and revise them weekly to build confidence.

AP ICET Mathematical Ability Sample Questions: Statistical Ability

The statistical ability section of the AP ICET examination includes questions from topics such as probability, concepts such as mean, median and mode, harmonic and geometric mean, standard deviations and so on. While analysing the previous year's question papers, it can be observed that the questions are direct and easily solvable as it is not calculation intensive. Some of the AP ICET statistical ability sample questions are given below. In the AP ICET 2025 question paper, the candidates must answer 10 questions under this topic of the Mathematical ability section. With enough practice, the candidates can easily solve 7-9 questions in this section. The given below AP ICET mathematical ability model questions on the statistical ability topic are concatenated from the previous year's question papers and sample papers.

Question 1:
What is the Geometric Mean of 12, 30, and 75?

Options:

1. 25

2. 60

3. 30

4. 28

Correct Option:
3. 30

Explanation:
The formula for the geometric mean of n numbers is:

Geometric Mean = (x₁ × x₂ × ... × xn)ⁱ⁄ⁿ

For the numbers 12, 30, and 75:

Geometric Mean = (12 × 30 × 75)¹/³

First, multiply the numbers:

12 × 30 × 75 = 27000

Now, take the cube root:

Geometric Mean = (27000)¹⁄³ = 30

Thus, the geometric mean of 12, 30, and 75 is 30. Hence, the correct answer is 30.

Question 2:
What is the Harmonic Mean of 3, 4, 5, and 6?

Options:

1. 5.21

2. 4.21

3. 4.52

4. 5.32

Correct Option:
2. 4.21

Explanation:
The formula for the Harmonic Mean (HM) of n numbers is:

HM = n / (1/x₁ + 1/x₂ + ... + 1/xn)

For the numbers 3, 4, 5, and 6:

HM = 4 / (1/3 + 1/4 + 1/5 + 1/6)

First, calculate the sum of the reciprocals:

1/3 + 1/4 + 1/5 + 1/6 = 0.3333 + 0.25 + 0.2 + 0.1667 = 0.95

Now, calculate the harmonic mean:

HM = 4 / 0.95 = 4.21

Hence, the harmonic mean of 3, 4, 5, and 6 is 4.21. Therefore, the correct answer is 4.21.

Question 3:
The median of 260, 240, 210, 210, 190, 180, 220, 230, 250 is?

Options:

1. 225

2. 230

3. 220

4. 235

Correct Option:

1. 225

Explanation:
To find the median:

1. First, arrange the numbers in ascending order: 180, 190, 210, 210, 220, 230, 240, 250, 260

2. The median is the middle value in an odd-numbered set. In this case, there are 9 numbers, so the middle number is the 5th value.

Thus, the median is 220. Therefore, the correct answer is 220.

Question 4:
The Standard Deviation of 2, 4, 6, 8, 10 is?

Options:

1. √6

2. 2√3

3. 2√2

4. 3√2

Correct Option:
3. 2√2

Explanation:
To calculate the Standard Deviation, follow these steps:

1. Find the Mean (Average):
   Mean = (2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6

2. Calculate the squared differences from the mean:
   (2 - 6)² = 16
   (4 - 6)² = 4
   (6 - 6)² = 0
   (8 - 6)² = 4
   (10 - 6)² = 16

3. Find the variance (average of squared differences):
   Variance = (16 + 4 + 0 + 4 + 16) / 5 = 40 / 5 = 8
   
   

4. Take the square root to get the standard deviation:
   Standard Deviation = √8 = 2√2

Question 5:
The mean deviation of 3, 4, 5, 6, 7 is?

Options:

1. 3.5

2. 3.2

3. 2.5

4. 1.2

Correct Option:
4. 1.2

Explanation:
To calculate the mean deviation, follow these steps:

1. Find the Mean (Average):
   Mean = (3 + 4 + 5 + 6 + 7) / 5 = 25 / 5 = 5

2. Calculate the absolute deviations from the mean:
   |3 - 5| = 2
   |4 - 5| = 1
   |5 - 5| = 0
   |6 - 5| = 1
   |7 - 5| = 2

3. Find the mean of these absolute deviations:
   Mean Deviation = (2 + 1 + 0 + 1 + 2) / 5 = 6 / 5 = 1.2

Hence, the mean deviation of 3, 4, 5, 6, 7 is 1.2. Therefore, the correct answer is 1.2.

Question 6:
When two dice are thrown, what is the probability of getting the sum 7?

Options:

1. 5/6

2. 1/6

3. 5/36

4. 1/9

Correct Option:
2. 1/6

Explanation:
When two dice are thrown, the total possible outcomes are 6 × 6 = 36, since each die has 6 faces.

The outcomes that give a sum of 7 are:

• (1, 6)

• (2, 5)

• (3, 4)

• (4, 3)

• (5, 2)

• (6, 1)
  
  

There are 6 favorable outcomes that result in a sum of 7.

Therefore, the probability of getting a sum of 7 is:

Probability = Favorable outcomes / Total outcomes = 6 / 36 = 1 / 6

Thus, the correct answer is 1/6.

Question 7:
A coin is tossed 6 times. What is the probability of getting heads at least once?

Options:

1. 33/64

2. 27/64

3. 1/64

4. 63/64

Correct Option:
4. 63/64

Explanation:
When a coin is tossed 6 times, there are a total of 2⁶ = 64 possible outcomes (since there are 2 possible outcomes for each toss: heads or tails).

The probability of not getting heads in a single toss is 1/2.
For 6 tosses, the probability of not getting heads at all (i.e., getting tails on every toss) is:

(1/2)⁶ = 1/64

Now, the probability of getting heads at least once is the complement of the probability of getting no heads at all:

Probability = 1 - Probability of no heads = 1 - 1/64 = 63/64

Thus, the correct answer is 63/64.

AP ICET Statistical Ability Tips

Here are a few tips and tricks that the candidates can use to enhance their AP ICET mathematical ability’s statistical ability section.

• A lot of questions are asked from basics of measures of central tendencies such as mean, median, mode and standard deviation. This is also evidently seen in a lot of AP ICET mathematical ability sample questions. Hence, the candidates should be thorough with their basics while preparing for the mathematical ability section.

• Since the statistics concepts involve a lot of equations and formulas, it is beneficial for the candidates to keep track of these using handbooks or flashcards.

• The candidates should also rely on mental math techniques to speed up their calculation skills and save time during the examination.

• Practicing past papers helps in understanding the pattern and types of statistical questions asked. This should always be prioritised after the candidates are done with their AP ICET syllabus.

• The candidates should also always review their mistakes and work on them. Understanding the weak areas and working on them would help the candidates to enhance their AP ICET 2025 scores.

AP ICET 2025 Preparation Books

Some of the suggested books for the AP ICET 2025 exam preparation are listed below.

AP ICET 2025 Practice Resources by Careers360

Some of the effective AP ICET preparation resources designed by Careers360 is provided in the table below.