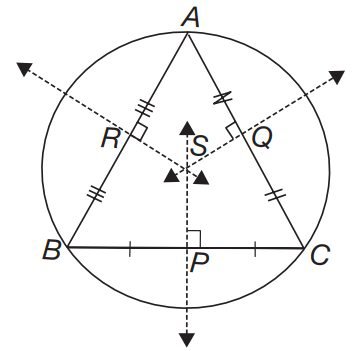
Circumcircle: There here is a unique circle passing through the three vertices A, B and C of the triangle. This circle is called the circumcircle of the ∆ ABC. Its center and radius are called respectively the circumcentre and the circumradius of the triangle.

Circum-centre: The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circumcenter. The circumcenter is equidistant from all the vertices of the triangle.

Let a, b, and c denote the triangle's three sides, and let A denote the area of the triangle. Then, the measure of the circumradius (R) of the triangle is given by $\mathrm{\mathbf{R}=\frac{abc}{4\mathbf{A}}}$ .

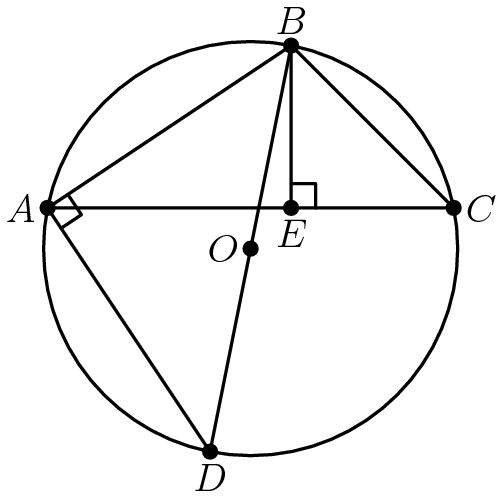
Let AB = c, BC = a, AC = b, BE = h, and BO = R. We know that $\angle\text{BAD}$ is a right angle because BD is the diameter. Also, $\angle\text{ADB}=\angle\text{BCA}$ because they both subtend arc AB. Therefore, $\Delta\text{BAD}\sim\Delta\text{BEC}$ by AA similarity.

So we have

$\\\mathrm{\;\;\;\;\;\frac{B D}{B A}=\frac{B C}{B E}}\\\\\text{or}\;\;\;\mathrm{\frac{2 R}{c}=\frac{a}{h}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ldots(1)$

And as you remember that area of the triangle [ABC] = $\mathrm{\frac{1}{2}\times base \times height}=\mathrm{\frac{1}{2}\times AC \times BE=\frac{bh}{2}}$

$\\\mathrm{Let,\;[ABC]=\frac{bh}{2}}\Rightarrow \mathrm{h=\frac{2[ABC]}{b}}$

Put the value of h in (1), we get

$\\\mathrm{\frac{2R}{c}=\frac{a}{\frac{2[ABC]}{b}}}$

and then simplifying to get

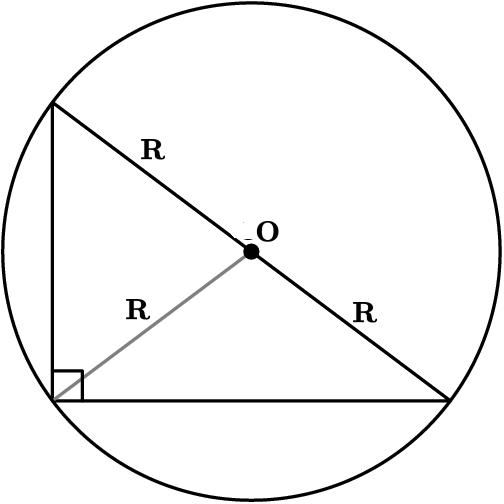
$\mathrm{R=\frac{a b c}{4 \times[A B C]} \text { or }[A B C]=\frac{a b c}{4 R}}$

Circumradius of Right Angle Triangle

The hypotenuse of the triangle is the diameter of its circumcircle, and the circumcenter is its midpoint, so the circumradius is equal to half of the hypotenuse of the right triangle.

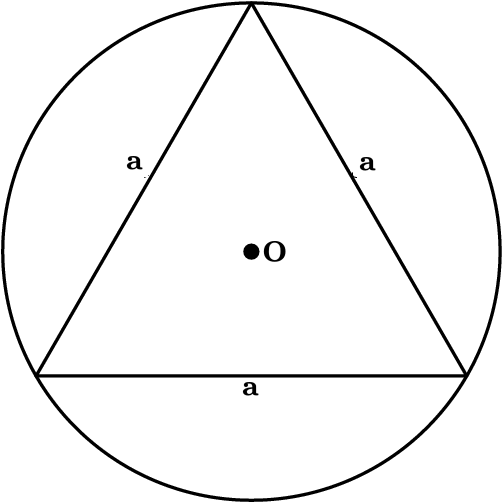
Circumradius of Equilateral Angle Triangle

$\mathrm{\mathbf{R}=\frac{a}{\sqrt3}}$

where a is the length of a side of the triangle.

Incircle: The circle inscribed in a triangle is the largest circle contained in the triangle; it touches (or tangent to) the three sides of the triangle. The center of the incircle is called the incenter and the radius of the incircle is called inradius and it is denoted by 'r'.

Incenter: The angle bisectors of the triangle are concurrent and the point of concurrence is called the in-center and is usually denoted by I. I is equidistant from the sides of the triangle.

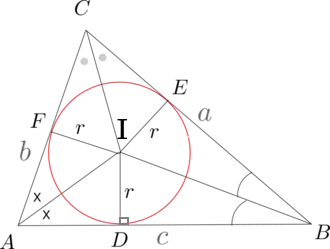
$\mathbf{r}=\mathrm{\frac{area\;of\; \Delta ABC}{semi\; perimeter \;of\;\Delta ABC}}$

Proof:

Add in the incircle and drop the altitudes from the incenter to the sides of the triangle. Also, draw the lines AI, BI and.CI After this AB, AC, and BC are the bases of $\mathrm{\Delta AIB,\;\Delta AIC}$ , and $\mathrm{\Delta BIC}$ respectively. But they all have the same height (the inradius), So,

$\begin{aligned} \mathrm{Area \;of\;\Delta ABC}&=\mathrm{Area\;of\;\left ( \Delta AIB+\Delta AIC+\Delta BIC \right )}\\&=\frac{1}{2}\times AB\times ID +\frac{1}{2}\times AC\times IF+\frac{1}{2}\times BC\times IE \\&=\frac{1}{2}\times ID\times\left ( AB+BC+CA \right )\\&=\frac{1}{2}\times r\times\left ( a+b+c \right ) \end{aligned}$

Since, ID = IF = IE = r = inradius and let ½(a + b + c) = s = semiperimeter of triangle, then we get

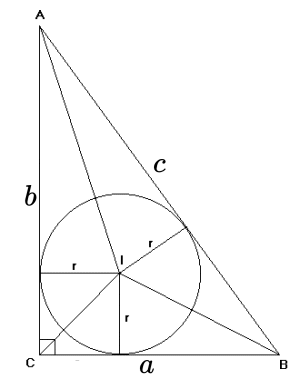
$\\\mathrm{Area \;of\;\Delta ABC=r\times s}\\\\\mathrm{r=\frac{Area \;of\;\Delta ABC}{s}}$

Inradius of Right Angle Triangle

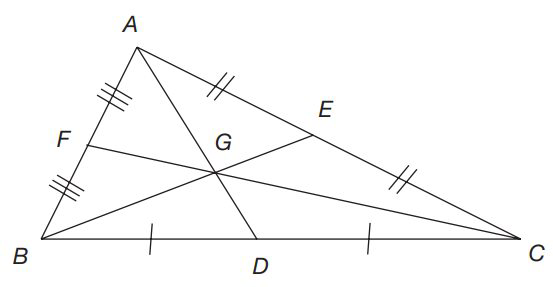
$\mathrm{Inradius\; }\mathbf{(r)}=\mathrm{\frac{1}{2}\left ( a+b-c \right )}$

Centroid: The medians of a triangle are concurrent and the point of concurrence of the medians of a triangle is called the centroid and it is usually denoted by G. The centroid divides each of the medians in the ratio 2 : 1, i.e., in the figure given below, AG : GD = BG : GE = CG : GF = 2 : 1.

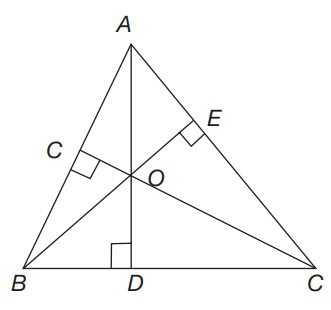
Ortho-centre: The altitudes of the triangle are concurrent and the point of concurrence of the altitudes of a triangle is called ortho-centre and is usually denoted by O.