• Management and Business Administration
  • Engineering and Architecture
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Common Mistakes in CAT Reading Comprehension Questions; Avoid These RC Errors for CAT 2026
  1. Home
  2. CAT
  3. Study Material
  4. CAT Equation of Tangent - Practice Questions & MCQ

CAT Equation of Tangent - Practice Questions & MCQ

Edited By admin | Updated on Oct 04, 2023 04:20 PM | #CAT

Quick Facts

  • 5 Questions around this concept.

Solve by difficulty

QuestionEASY

Find the equation to the tangent of circle x^2+y^2=25 at the point (4, 3).

View Solution

Equation of tangent to the circle x^2+y^2+4x+4y+16=0 at point (x_1,y_1) is:

View Solution

Concepts Covered - 1

Equation of Tangent

In the previous concept we studied that the tangent at any point of a circle is perpendicular to the radius through the point of contact. We will use this concept to find the equation of a tangent to a circle.

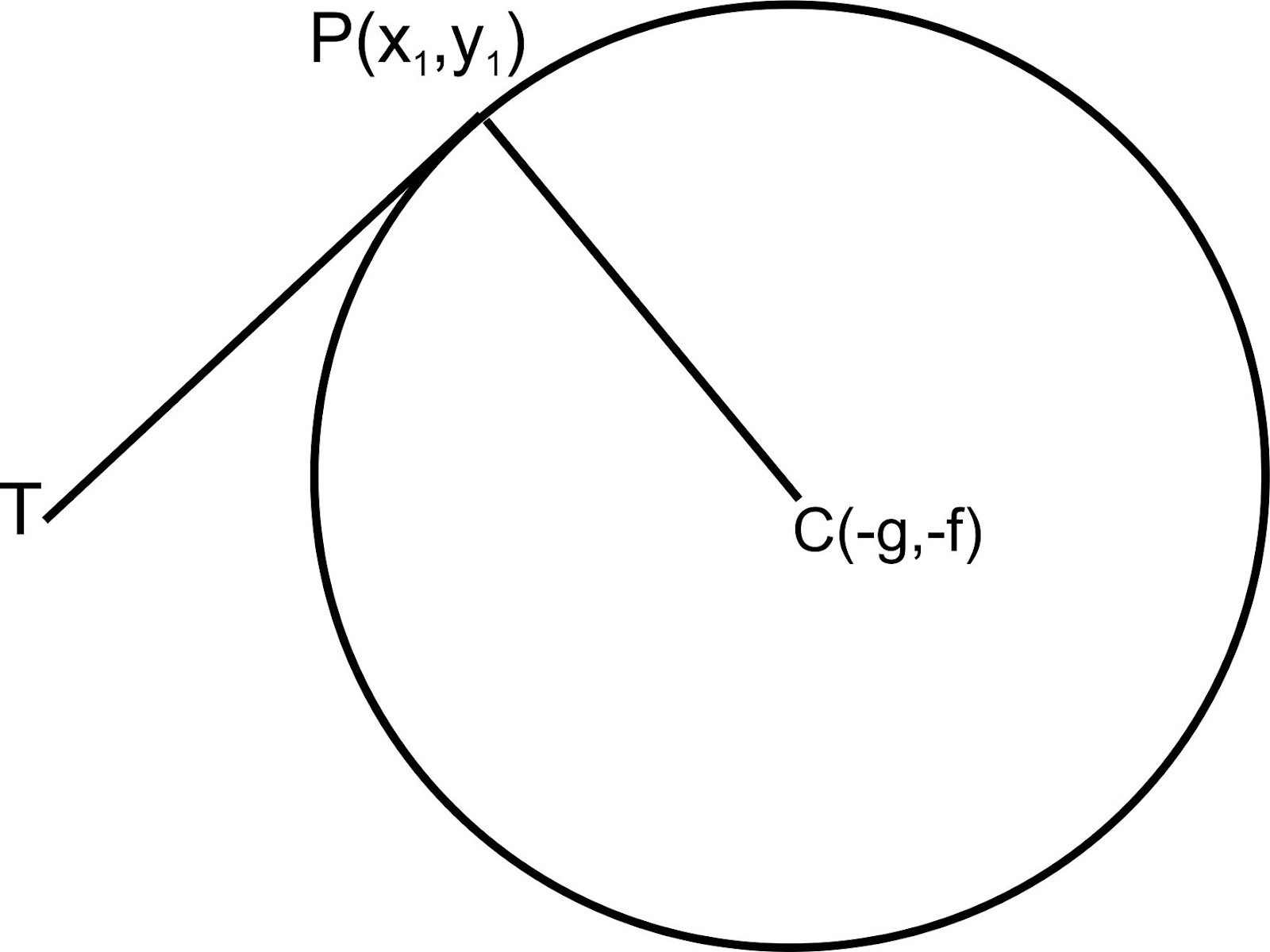
Let the circle with center C(-g, -f) and a tangent PT with Point P (x1, y1) lies on the circle. From the theorem, PT is perpendicular to CP.

\text { Slope of } \mathrm{CP}=\frac{\mathrm{y}_{1}-(-\mathrm{f})}{\mathrm{x}_{1}-(-\mathrm{g})}=\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{x}_{1}+\mathrm{g}}

Also we know that if two lines are perpendicular, then multiplication of their slopes is equal to -1.

i.e.

\\\text{(slope of PT) x (slope of CP) = -1} \\\Rightarrow \text{(slope of PT)}\times\left ( \frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{x}_{1}+\mathrm{g}} \right )=-1\\\Rightarrow \text{(slope of PT)}=-\left(\frac{\mathrm{x}_{1}+\mathrm{g}}{\mathrm{y}_{1}+\mathrm{f}}\right)

Now, the equation of the tangent at point P(x1, y1) is

\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\left(\mathrm{y}-\mathrm{y}_{1}\right)=-\left(\frac{\mathrm{x}_{1}+\mathrm{g}}{\mathrm{y}_{1}+\mathrm{f}}\right)\left(\mathrm{x}-\mathrm{x}_{1}\right) \\ \Rightarrow \quad\left(\mathrm{y}-\mathrm{y}_{1}\right)\left(\mathrm{y}_{1}+\mathrm{f}\right)+\left(\mathrm{x}_{1}+\mathrm{g}\right)\left(\mathrm{x}-\mathrm{x}_{1}\right)=0 \\ \Rightarrow \quad \mathrm{xx}_{1}+\mathrm{yy}_{1}+\mathrm{gx}+\mathrm{fy}=\mathrm{x}_{1}^{2}+\mathrm{y}_{1}^{2}+\mathrm{gx}_{1}+\mathrm{fy}_{1}

Let’s simplify the above equation

add \mathrm{g x_{1}+f y_{1}+c} both side, we get

\\\Rightarrow \quad \mathrm{x x_{1}+y y_{1}+g\left(x+x_{1}\right)+f\left(y+y_{1}\right)+c=x_{1}^{2}+y_{1}^{2}+2 g x_{1}+2 f y_{1}+c}\\\Rightarrow\mathrm{\;\;\;}\mathrm{ x x_{1}+y y_{1}+g\left(x+x_{1}\right)+f\left(y_{1}+ y\right)+c=0 }

As we know that the general equation of circle x2+y2+2gx+2fy+c=0 and the point (x1,y1) lies on the circumference of the circle.

Also \mathrm{x}_{1}^{2}+\mathrm{y}_{1}^{2}+2 \mathrm{gx}_{1}+2 \mathrm{fy}_{1}+\mathrm{c}=0  as point (x1,y1) lies on the circle

Hence, \mathrm{x x_{1}+y y_{1}+g\left(x+x_{1}\right)+f\left(y_{1}+ y\right)+c=0} is the equation of tangent at point (x1,y1) of circle having centre at (-g, -f). 

The equation of the tangent to the circle \mathrm{x^2+y^2=a^2} at point (x1,y1) is \mathrm{xx_1+yy_1=a^2}.

Study other Related Concepts

CAT Equation of Tangent Current Topic

CAT Basic Terms and Definitions of Lines and Angles
CAT Various Types of Angle
CAT Linear Pair of Angles
CAT Vertically Opposite Angles
CAT Corresponding Angle Axioms
CAT Alternate Interior Angle Theorem
CAT Interior Angle Theorem
CAT Parallel and a Transversal Lines
CAT Introduction to Triangles
CAT Congruence of Triangles

"Stay in the loop. Receive exam news, study resources, and expert advice!"

Get Answer to all your questions

MBA/PGDM Admissions OPEN

Amity University-Noida MBA Admissions 2026
Apply

Ranked among top 10 B-Schools in India by multiple publications | Top Recruiters-Google, MicKinsey, Amazon, BCG & many more.

Great Lakes Institute of Management PGPM Admissions 2026
Apply

Extended Application Deadline: 15th Feb | Globally Recognized by AACSB (US) & AMBA (UK) | 17.8 LPA Avg. CTC for PGPM 2025

SDA Bocconi IMB Admissions 2026
Apply

Applications Deadline - 23rd March 2026 | Offers full-time PGP in International Master in business (IMB) Equivalent to MBA under following specializations Marketing, HR, Operations, and many more

Paari school of Business SRM (A.P) MBA Admissions 2026
Apply

MBA Admissions Open 2026 | #1st in the Emerging B-School Category in South India by OUTLOOK | Average CTC 8.51 LPA |

BIMTECH PGDM Admissions 2026
Apply

AACSB Accredited | Highest CTC: 22 LPA

Poddar Business School PGDM Admissions 2026
Apply

Highest CTC 24 LPA | Average CTC 8.5 LPA | 1600+ Recruiters | 165+ Corporates Linkages

View all Application Forms

Student Community: Where Questions Find Answers

Ask and get expert answers on exams, counselling, admissions, careers, and study options.
Download Careers360 App
All this at the convenience of your phone

  • Regular Exam Updates

  • Best College Recommendations

  • College & Rank predictors

  • Detailed Books and Sample Papers

  • Question and Answers

Scan and download the app

OR

College Predictor