The Indian Institute of Management (IIM) organizes the IPMAT (Integrated Program in Management Aptitude Test), which is administered in an electronic format. Reviewing past IPMAT question papers and sample papers helps students grasp the test format, question kinds, subjects covered, and difficulty level. IPMAT 2024 Exam was taken on May 23, 2024. Candidates may download previous question papers to practice and improve their speed and accuracy. This article also tells you where to get IPMAT question papers with answers in PDF format to help you prepare.
IPMAT Question Paper: Sample QA Questions with Solutions
IPMAT Syllabus:
IPMAT Previous Year papers
Strategies for Solving Previous Papers
Benefits of Solving IPMAT Previous Papers
IPMAT Question Papers: Download Free Last Year's Question Papers With Answer Key PDF
IPMAT Question Papers
To crack IPMAT 2025 with excellent scores, past year papers and practice exams can really assist well. The previous year's IPMAT question papers help candidates assess their aptitude and test-taking skills and provide them with valuable insights on how to approach the IPMAT exam. By solving the IPMAT last year paper and using IPMAT Mock Test PDFs candidates can tremendously improve their time management skills, speed, and accuracy.
Download IPMAT Previous Year Question Papers PDF
Download the free IPMAT exam official question papers and practice with them to ramp up your IPMAT preparation.
Candidates who want to appear for the IPMAT Exam must be familiar with the structure of the question paper. Below is an overview of the IPMAT question paper based on the previous year questions.
The overall difficulty level of the IPMAT exam questions paper would be moderate.
There will be three sections - two sections have MCQs questions while QA (SA) will have Non-MCQs questions
The duration of the exam is 120 minutes, with each section having 40 minutes.
There will be logic-based and a few arithmetic questions. The higher mathematics component is high.
The exam will also have many language and grammar-based questions.
IPMAT Exam Sample/Question Papers
IPMAT previous years Questions and Sample Papers to boost your preparation.
Short-answer questions and multiple-choice questions
IPMAT Indore marking scheme
Candidates will be awarded 4 marks for each correct answer and there will be -1 negative marking for wrong answers
IPMAT total marks
400 marks
How to Use IPMAT Question Papers
Using IPMAT previous year papers with answers as a part of your preparation strategy can be highly beneficial. By keeping the following points in mind, you can maximize the benefits:
1. Understand IPMAT Exam Pattern
Analyze the distribution of questions across IPMAT sections (Quantitative Ability, Verbal Ability, and Logical Reasoning) and their respective weightage. This will help you understand which areas/topics are more frequently tested and prioritize your preparation accordingly.
2. Identify Important Topics for IPMAT
By going through IPMAT question paper pdfs, you can identify recurring topics or types of questions that are commonly asked. Focus more on these areas as they are likely to be important. In these papers, you'll find IPMAT Geometry questions, IPMAT Log questions, IPMAT percentage questions, IPMAT algebra questions, and IPMAT trigonometry questions. In the verbal ability questions, you can find IPMAT grammar syllabus questions.
3. Time Management Practice
Solve the IPMAT previous year papers within the stipulated time limit to practice time management. This will help you improve your speed and accuracy, crucial for competitive exams like IPMAT.
4. Make Notes
Good notes can make a good understanding of concepts. While solving the IPMAT previous year's question papers, you must make notes of easy and difficult questions so you can make your preparation ahead accordingly and keep revising difficult concepts. The notes can be used as a quick reference guide.
IPMAT Question Paper: Sample QA Questions with Solutions
IPMAT Exam 2019
Q1. The sum of the interior angles of a convex n-sided polygon is less than 2019. The maximum possible value of n is ______
Ans: Sum of the interior angles of polygon = (n-2). 180
=> (n-2). 180 < 2019
=> 180n – 360 < 2019
=> 180n < 2379
=> n < 2379/180
=> n < 13.21 {No. of sides must be an integer}
so maximum possible value of n = 13.
Q2. Three friends divided some apples in the ratio 3:5:7 among themselves. After consuming 16 apples they found that the remaining number of apples with them was equal to largest number of apples received by one of them at the beginning. Total number of apples these friends initially had was _____
Ans: Let three friends are A, B, C, A: B: C = 3:5:7,
So, A = 3x, B = 5x, C = 7x, Total apples = 15x
After consuming 16 apples remaining apples = 15x -16;
As given in the question, remaining apples = largest number of apples received by one of them at the beginning.
So, 15x-16 = 7x
8x = 16; x = 2
So, total number of apples = 15x = 15 x 2 = 30.
Q3. A shopkeeper reduces the price of a pen by 25% as a result of which the sales quantity increased by 20%. If the revenue made by the shopkeeper decreases by x% then x is
Ans: A = B X C
If percentage change in B and C is x% & y% then effective percentage change in A will be equal to (x + y + x.y/100) %. [Successive percentage change]
Revenue = Price of pen x Sales quantity
Percentage change x%+25%+20%
As per above explained formula percentage change in revenue = (25+20+25 x 20/100) %
X % = 50%.
Q4. The average of five distinct integers is 110 and the smallest number among them is 100. The maximum possible value of the largest integer is _____
Ans: Let five distinct integers are A,B,C,D & E, where A is smallest and E is largest.
As given, A=100
Average = 110
(A + B + C + D + E)/5 = 110
A + B + C + D + E = 550 ………..Equation (1)
Amity University Gurgaon BBA Admissions 2025
Ranked as India’s #1 Not for profit pvt. University by India Today
For maximum value of E, other values must be minimum;
As all integers are distinct; If A = 100, B = 101, C = 102, D = 103
On putting value in equation (1), E = 550 – 100 -101- 102 – 103 = 144.
Q5. The number of whole metallic tiles that can be produced by melting and recasting a circular metallic plate, if each of the tiles has a shape of a right-angled isosceles triangle and the circular plate has a radius equal in length to the longest side of the tile (Assume that the tiles and plate are of uniform thickness, and there is no loss of material in the melting and recasting process) is ______
Ans:
Assume that the tiles and plate are of uniform thickness, and there is no loss of material in the melting and recasting process.
Let radius of circle = r
Length of longest side of right-angled isosceles triangle = r {Hypotenuse}
So, area of the triangle = (Hypo.)2 / 4 = r2/4
No. of triangles(N) X Area of triangle = Area of metallic circular plate
N.r2/4 = πr2
N = 4.π = 4 x 3.14 = 12.56
So, number of whole metallic tiles that can be produced by melting and recasting a circular metallic plate = 12.
Q6. If the compound interest earned on a certain sum for 2 years is twice the amount of simple interest for 2 years, then the rate of interest per annum is percent a) 200% b) 2% c) 4% d) 400%
Correct option: a)
Ans: let P= Principal, R = Rate of interest; Time = 2 years (given)
Compound Interest (C.I.) = 2 x Simple Interest (S.I.)
P [1+R/100]2 – P = 2 x P.R.T/100
P[{1+R/100}2 - 1] = 2 x P. R. 2/100
1 + 2R/100 + R2/1002 – 1 = 4. R/100
R/100 [2 + R/100] = 4. R/100
R = 200
Q7. The maximum value of the natural number n for which 21n divides 50! is a) 6 b) 7 c) 8 d) 9
Correct option: c)
Ans:
To factorize 50!, IGP (Index of greatest power) is found out for prime numbers. But in this case divisor is 21n, (3 x 7)n so only IGP of 3 & 7 is required.
IGP of 3 in 50! = 22
IGP of 7 in 50! = 8
50! = 322 x 78
50! / 21n = 50! / (3 x 7)n;
In this case numerator has max 8 power of 7, so denominator can’t have more than 8 power of 7
So, maximum possible value of n = 8
Q8. Placing which of the following two digits at the right end of 4530 makes the resultant six-digit number divisible by 6,7 and 9?
a) 96
b) 78
c) 42
d) 54
Correct option: a)
Ans:
On putting values as per options:
a. 453096- Sum of digits = 27
b. 453078- Sum of digits = 27
c. 453042- Sum of digits = 18
d. 453054- Sum of digits = 21
On the basis of this we can say that option (d) is eliminated as sum of digits is not divisible by 9 but all other numbers satisfy condition as per divisibility rule of 6 & 9.
Now, for 7 we can divide other three options and check.
Q9. The inequality log23x-12-x<1 holds true for a) x13,1 b) x13,2 c) x0,13∪(1,2) d) x∈(-∞,1)
Correct option: d)
Ans: log23x-12-x<1
=> 3x-12-x < 21
=> 3x-1 < 2 (2-x) => 3x-1 < 4 – 2x
=> 5x < 5 => x < 1
Q10. The number of terms common to both the arithmetic progressions 2,5,8,11,...., 179 and 3,5,7,9,....., 101 is
Common difference d = lcm {d1, d2} = lcm {3,2} = 6
From both sequences, first common term 5, then next term will be 11.
So, sequence 5,11,17,……..
nth term must be less than or equal to 101 {which is last & least term out of both sequences}
an <= 101
5 + (n-1). 6 <= 101
(n-1) <=16
n <=17 ; so, No. of common terms of both sequences = 17
IPMAT Exam 2020
Q1. The probability that a randomly chosen factor of 1019 is a multiple of 1015 is a) 125 b) 112 c) 120 d) 116
Correct option: d)
Ans: 1019 = 219 x 519
Total no. of factors = (19+1). (19+1) = 400
To find out no. of factors of 1019 which are multiple of 1015, find the factors of remaining part in no. after excluding 1015.
1019 = 1015 x 104 = 1015 x 24 x 54
No. of factors of 1019 which are multiple of 1015= (4+1). (4+1) = 25
Probability = favorable outcomes/ total no. of outcomes
= No. of factors of 1019 which are multiple of 1015 / Total no. of factors
= 25/400 = 1/16
Q2. The number of acute angled triangles whose sides are three consecutive positive integers and whose perimeter is at most 100 is
a) 28
b) 29
c) 31
d) 33
Correct option: b)
Ans:
If three sides are consecutive, then possible sides of triangle are (1,2,3), (2,3,4), (3,4,5), (4,5,6)…………..
For acute angle triangle, triangle should follow following two conditions:
Sum of any two sides must be greater than the third one.
So, as per this condition (1,2,3) can’t be sides of any triangle.
Square of the greatest side must be less than the sum of squares of other two sides.
Ex: If sides of triangle are (a,b,c), where c is the greatest side then for acute angle triangle c2 < a2 + b2.
Hence, (2,3,4) & (3,4,5) doesn’t satisfy the condition of acute angle triangle.
Sides Perimeter (Sum of sides)
(1,2,3) 6
(2,3,4) 9
(3,4,5) 12
.
.
.
(32,33,34) 99
Out of these pairs first doesn’t satisfy as per condition (i) and second & third pair doesn’t satisfy the condition (ii) given and required.
So, no. of possible pairs of triangles is 29.
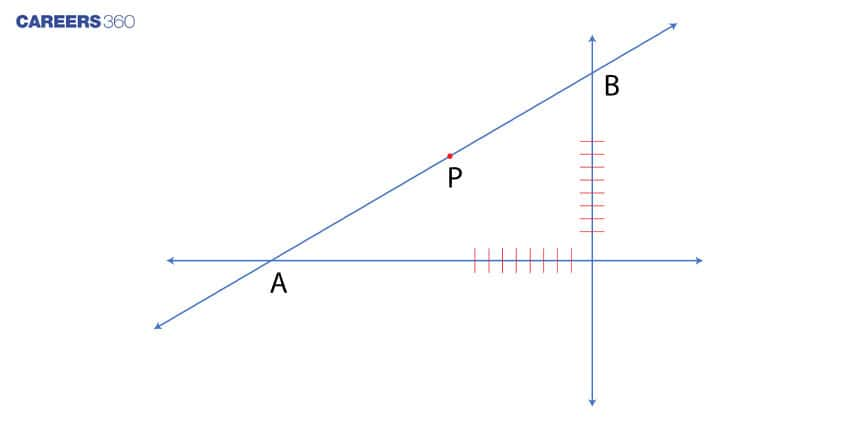
Q3. The equation of the straight line passing through the point P(-5,1), such that the portion of it between the axes is divided by the point P in to two equal halves, is a) 10y-8x=80 b) 8y+10x=80 c) 10y+8x=80 d) 8y+10x+80=0
Correct option: a)
Ans:
The point P divides AB into 2 halves. AP = PB A is on the x axis, Hence Point A (h,0) B is on the Y axis, Hence Point B (0,k)
Using midpoint formula.
[(ℎ+0)/2,(?+0)/2] = (-5 , 4)
h/2 = - 5 => h = -10
k/2 = 4 => k = 8
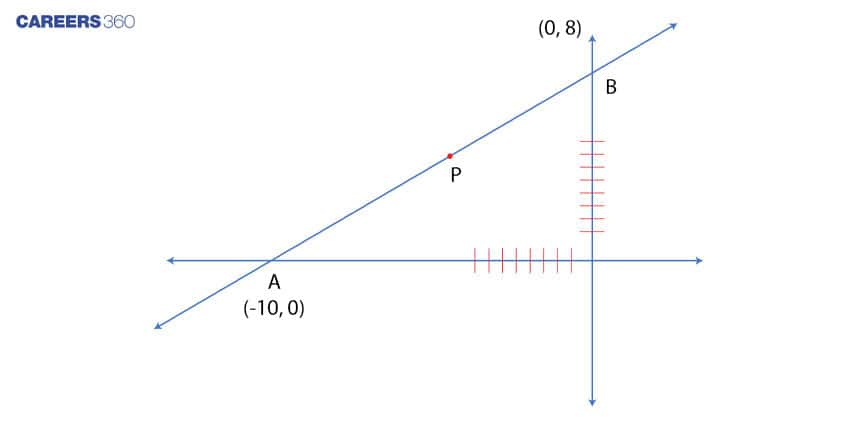
Hence the Y intercept is 8 and X intercept is - 10. x/(-10) + y/8 = 1 -8x + 10y = 80 The equation is -8x + 10y = 80
Q4. A man is known to speak the truth on an average 4 out of 5 times. He throws a die and reports that it is a five. The probability that it is actually a five is a) 49 b) 59 c) 415 d) 215
Correct option: d)
Ans: Probability of speaking truth P(T) = 4/5
Probability of appearing 5 on dice P(5) = 1/6
He throws a die and reports that it is a five, the probability that it is actually a five is = P(T) x P(5) = 4/5 x 1/6 = 2/15
Q5. Consider the following statements: (i) When 0<x<1, then 11+x<1-x+x2. (ii) When 0<x<1, then 11+x>1-x+x2. (iii) When -1<x<0, then 11+x<1-x+x2. (iv) When -1<x<0, then 11+x>1-x+x2. Then the correct statements are a) (i) and (ii) b) (ii) and (iv) c) (i) and (iv) d) (ii) and (iii)
Correct option: c)
Ans:
Let’s compare these 2 inequalities, 11+x<1-x+x2.
1-x + x2 – (1/1+x) > 0
(1 + x3 -1)/(1+x) > 0
x3/(1+x) > 0
This inequality holds good when x is positive and when both numerator & denominator are negative. Hence the correct answer is (i) and (iv).
Q6. In a division problem, product of quotient and the remainder is 24 while their sum is 10. If the divisor is 5 then dividend is ______
Ans: Dividend (N) = Quotient(Q) x Divisor(D) + Remainder (R)
Given- Q x R = 24………. Equation (1)
Q + R = 10………Equation (2)
By solving both equations (Either proper method or hit & trial)
Two possible values, (i) Q = 6 & R = 4
(ii) Q = 4 & R = 6 {This is not possible as remainder must be less than divisor}
So, only possible values are Q=6 & R=4,
So, N = Q X D + R
N = 6 x 5 + 4 = 34.
Q7. Ashok purchased pens and pencils in the ratio 2:3 during his first visit and paid Rs. 86 to the shopkeeper. During his second visit, he purchased pens and pencils in the ratio 4:1 and paid Rs. 112. The cost of a pen as well as a pencil in rupees is a positive integer. If Ashok purchased four pens during his second visit, then the amount he paid in rupees for the pens during the second visit is ______
Ans:
First Visit
Ratio of pen: pencil is 2:3 and he spends Rs 86
Let price of pen be 'x' and price of pencil be 'y', as nothing is given related to no. of pen and pencils, so there are multiple possibilities-
Ratio of pen and pencil is 4:1 and he spends Rs 112 It is given that he purchased 4 pens. Hence, he purchased 4 pens and 1 pencil (as per ratio) Then, 4x + y = 112
Since, from second visit, 4 pen and a pencil costs Rs 112 so, if more than 4 pens and 1 pencil are bought then the cost must be more than 112.
As per above discussion, only 2x + 3y = 86 is possible in first visit.
From first visit---- 2x + 3y = 86 From second visit---- 4x + y = 112 On solving both equations, We get y = 12, x = 25.
He paid Rs 100 during his second visit for the pens.
Q8. In a four-digit number, the product of thousands digit and unit digit are zero while their difference is 7. Product of the middle digits is 18. The thousands digit is as much more than the unit digit as the hundreds digit is more than the tens digit. The four-digit number is_____
Ans:
In the given 4-digit number, the product of thousands digit and unit digit is zero. If product of two digits is zero that means either both digits are zero or one of them is zero. As thousandth digit cannot be zero, then unit digit is zero. __ __ __ 0
Given: Thousands digit and digit difference is 7, that means thousands digit is 7 7 __ __ 0
Given: Product of middle digits is 18 and difference is same as between thousands and unit digit. So, product of middle digits is 18 and difference is 7. Only two digits are possible 9 and 2.
As given hundreds digit is more than the tens digit. So hundreds digit is 9 and tens digit is 2
So, no. is 7920.
Q9. Ashok started a business with a certain investment. After few months, Bharat joined him investing half amount of Ashok's initial investment. At the end of the first year, the total profit was divided between them in ratio 3:1. Bharat joined Ashok after
Ans:
Ashok Bharat
Investment 2x (let) x
Amount 12 months y months
Profit Ratio = (Investment x Amount) Ratio
Ashok Bharat
Profit Ratio = 2x. 12 : x.y
3 :1 = 24 : y
On solving this, y = 8 months.
Q10. Out of 13 objects. 4 are indistinguishable and rest are distinct, The number of ways we can choose 4 objects out of 13 objects is ____
No. of ways of choosing any no. of items out of identical items =1.
Case 1: All 4 are distinct- No. of ways = 9c4
Case 2: 1 identical & 3 objects are distinct- No. of ways = 9c3 x 1 {1 way of choosing 1 identical}
Case 3: 2 identical & 2 objects are distinct- No. of ways = 9c2 x 1 {1 way of choosing 2 identical}
Case 4: 3 identical & 1 objects are distinct- No. of ways = 9c1 x 1 {1 way of choosing 3 identical}
Case 5: 4 identical & 0 objects are distinct- No. of ways = 9c0 x 1 {1 way of choosing 4 identical}
So, total no. of ways = 9c4 + 9c3 + 9c2 + 9c1 + 9c0 = 126 + 84 + 36 + 9 + 1 = 256.
IPMAT Exam 2021
Q1. The number of positive integers which divide (1890)⋅(130)⋅(170) and are not divisible by 45 is _____
Ans:
N = (1890).(130).(170) = 23.33.53.7.13.17
Total no. of factors of N = (3+1) (3+1) (3+1) (1+1) (1+1) (1+1) = 512
To find out no. of factors of N which are divisible by 45, find no. of factors of the remaining part of no. after excluding 45-
N = 45 x 23.31.52.7.13.17
No. of factors of N divisible by 45 = no. of factors of remaining part (23.31.52.7.13.17)
= (3+1) (1+1) (2+1) (1+1) (1+1) (1+1) = 192
No. of positive integers which divide N (1890)⋅(130)⋅(170) and are not divisible by 45 is = Total no. of factors of N - No. of factors of N divisible by 45 = 512 – 192 = 320
Q2. The sum up to 10 terms of the series 1.3+5.7+9.11+… is
Ans:
= 1*3 + 5*7 + 9*11 ….. =(2 - 1)(2 + 1) + (6 - 1)(6 + 1) + (10-1)(10+1) + ….. = (22 - 12) + (62 - 12) + (102 - 12) + …… In this series, the common difference is 4.
2,6,10, ……..
The 10th term can be found to be , Sn = a + (n-1).d = [2 + 9*4] = 38 So the 10th term in the series can be rewritten as (382 - 12)
= 22 + 62 + 102 + … + 382 -1-1-1…..10 times = 4 [12 +32 +52 …..192 ] – 10 {Sum of squares of n odd terms= n(2n-1)(2n+1)/3} = 4 [1330] -10 =5310.
Q3. There are 5 parallel lines on the plane. On the same plane, there are n other lines which are perpendicular to the 5 parallel lines. If the number of distinct rectangles formed by these lines is 360, what is the value of n ?
Ans:
Let, the number of lines that are perpendicular to given 5 parallel lines is ‘n’. To make a rectangle we need 2 lines from each group.
Total no. of rectangles = 5C2 x nC2 => 5C2 xnC2 = 360 => 10 x n(n−1)/2 = 360 => n(n-1) = 72 => n = 9.
Q4. There are two taps, T1 and T2, at the bottom of a water tank, either or both of which may be opened to empty the water tank, each at a constant rate. If T1 is opened keeping T2 closed, the water tank (initially full) becomes empty in half an hour. If both T1 and T2 are kept open, the water tank (initially full) becomes empty in 20 minutes. Then, the time (in minutes) it takes for the water tank (initially full) to become empty if T2 is opened while T1 is closed is
Ans: Time Work (LCM of time) Efficiency
T1 30 min. 2
60 unit
T1+T2 20 min. 3
So, efficiency of T2 = (T1+T2 ) – T1 = 3 -2 = 1
Time taken by T2 to empty the full tank alone = work/efficiency = 60/1 = 60 min.
Q5. A class consists of 30 students. Each of them has registered for 5 courses. Each course instructor conducts an exam out of 200 marks. The average percentage marks of all 30 students across all courses they have registered for, is 80%. Two of them apply for revaluation in a course. If none of their marks reduce, and the average of all 30 students across all courses becomes 80.02%, the maximum possible increase in marks for either of the 2 students is
Ans:
Total marks in 1 course = 200
Total courses = 5
Total marks of all courses = 1000
Total marks of all students = 30 x 1000 = 30000
The change in the percentage of average marks scored is (80.02 - 80.00) % = 0.02% So the change in the marks is 30 x 1000 x 0.02% = 3 * 2 = 6 marks.
Q6. Let Sn be sum of the first n terms of an A.P. an. If S5=S9, what is the ratio of a3:a5 a) 9:5 b) 5:9 c) 3:5 d) 5:3
Correct option: a)
Ans:
Let terms of A.P. are, a1, a2, a3, a4, a5, a6, a7, a8, a9
Sum of A.P. = average x no. of terms
=> If no. of terms in A.P. are odd then average = middle-term.
a1, a2, a3, a4, a5 => Average = a3 S5 =a3 x 5
a1, a2, a3, a4, a5, a6, a7, a8, a9 => Average = a5 S9 = a5 x 9
as given, S5 = S9
=> a3 x 5 = a5 x 9
=> a3: a5 = 9 : 5
Q7. It is given that the sequence {xn} satisfies x1 = 0, xn+1 = xn + 1 + 2√(1+xn) for n = 1,2, . . . . . Then x31 is _______
Ans:
xn+1 = xn + 1 + 2√(1+xn) So x2 = x1 + 1 + 2√(1+x1) = 0 + 1 + 2√(1+0) x2 = 3 Similarly, x3 = x2 + 1 + 2√(1+x2) = 3 + 1 + 2√(1+3) x3 = 8 We see a pattern here that the nth term in the series is n2 - 1 And so the 31st term is 312 - 1 961 - 1 = 960.
Q8. The unit digit in (743)85-(525)37+(987)96 is a) 9 b) 3 c) 1 d) 5
Correct option: a)
Ans:
For unit digit, only unit digits are required.
= 385 - 537 + 796
{Cyclicity of 3 is 4, power 85/4 = rem. 1, so power is equivalent to 1}
{Cyclicity of 5 is 1, so all powers of 5 are equivalent to 1}
{Cyclicity of 7 is 4, power 96/4 = rem. 0, so power is equivalent to 4}
= 31 – 51 + 74
= 3 – 5 + 2401 = 3 – 5 +1 = -1 {If it is negative, then add 10 to get unit digit}
= -1 + 10 = 9.
Q9. If the angles A, B, C of a triangle are in arithmetic progression such that sin(2A + B) = 1/2 then sin(B + 2C) is equal to
a.−1/2
b. 1/2
c. −1/√2
d. 3/√2
Correct option: a)
Ans:
The angles A, B and C are in arithmetic progression and so the angles can be written as, (B-d), B, (B + d), where d is the common difference between the angles. The sum of the three angles of a triangle is 180 degrees and so,
B-d + B + B + d = 180° Or 3B = 180° B = 60°
Now, we also know that sin(2A + B) = 1/2 So, 2A + B = 30° or 150° But since we already know B = 60o and the angles cannot be negative, 2A + B cannot be 30° 2A + B = 150° 2A + 60o = 150° Or A = 45° => C = 75°
Now that we know all the angles we can find out the value of sin(B + 2C) B + 2C = 60 + 150 = 210° sin(210°) = sin(180° + 30°) = sin(30°) [sin(180° + θ) = -sin θ] = −1/2.
Q10. The highest possible value of the ratio of a four-digit number and the sum of its four digits is: a) 1000 b) 277.75 c) 900.1 d) 999
Correct option: a)
Ans:
Fraction = Four-digit number / the sum of its four digits
For making the fraction largest we need to have a big number in the numerator and a small number in the denominator. Let’s try 9999 in the numerator so the fraction becomes 9999/36 We can try to make denominator least, which can be 1.
The fraction becomes 1000/1 = 1000
IPMAT Syllabus:
The IPMAT exam generally assesses a candidate's aptitude in three main areas: Quantitative Ability (QA), Verbal Ability (VA), and Logical Reasoning (LR). Here's a detailed overview of the IPMAT syllabus for each section:
The IPMAT exam paper will have three sections - QA (multiple choice), VA (multiple choice) and QA (short answer). There is negative marking and each question carries 4 marks. For every wrong answer, one mark will be deducted.
IPMAT Previous Year papers
Practicing IPMAT previous year papers is essential for effective exam preparation as it gives candidates a clear understanding of the exam pattern, question types, and difficulty level. By working through these papers, candidates can identify important topics and areas where they need to focus more. It also helps in improving time management skills, as candidates can practice completing the paper within the allotted time, thereby enhancing their speed and accuracy
When addressing previous papers, it is critical to approach them strategically to maximize their usefulness. Start by establishing a timer to imitate the real test situation, which will help you improve your time management abilities. As you go through the paper, concentrate on recognizing the pattern and sorts of questions that arise frequently in exams. After finishing the task, carefully evaluate your answers, paying specific attention to errors. Analyze why you answered a question incorrectly and review the suggestions to improve your knowledge. It's also useful to divide questions into difficulty levels—easy, moderate, and hard—so you can concentrate on improving areas where you struggle. Regular practice with prior papers can help you identify patterns, enhance your speed, and gain confidence for the test.
Benefits of Solving IPMAT Previous Papers
Solving IPMAT past problems has various advantages that might greatly improve your test preparation. First, it gives a comprehensive grasp of the test format, allowing you to get acquainted with the various sorts of questions and the general framework. This familiarity alleviates exam-day worry and increases confidence. Regular practice with previous exams also helps with time management, since it allows you to determine how much time to devote to each part. Identifying repeated question patterns allows you to concentrate on important areas that are regularly evaluated. Reviewing your performance on these exams also helps to identify shortcomings and areas that need further focus, allowing for targeted revision. Overall, answering prior problems is an important step toward developing the skills and self-assurance required to succeed on the IPMAT test.
Frequently Asked Questions (FAQs)
1.Is 200 in IPMAT a good score?
200 in IPMAT can be considered an okayish score. TO be on the safer side, you must aim for a score of more than 230 marks.
2.Is IPMAT tough?
The difficulty level of IPMAT is moderate. However, you can expect to encounter some difficult questions.
3.Can I crack IPMAT exam in a month?
If you strategize your preparation in a proper way and consistently work hard, then you can expect to crack the IPMAT exam in a month.
4.Are 12th marks important for IPMAT?
Although the minimum criteria for class 12th is 60%, you will be in a better position if your 12th marks are good.
5.How can one start getting ready for IPMAT 2025
Before focusing on building a strong foundation in both verbal and numeric skills, familiarize yourself with the IPMAT syllabus. Create a consistent study regimen and ensure you comprehend the foundations of each subject.
6.What are some ways I can increase my exam speed and accuracy?
Practice past papers and mock exams frequently to increase accuracy and speed. Start with simple questions and work your way up to more complex ones. You can stay on track and earn as many points as possible in this method.
7.In the verbal and quantitative portions of the IPMAT, what should I concentrate on?
Key subjects in quantitative analysis include data interpretation, percentages, and profit and loss. Focus on sentence completion, vocabulary, and grammar when speaking. Being well-versed in these subjects will enable you to take the test with assurance.
8.As I prepare for the IPMAT, how can I balance my strengths and weaknesses?
Determine your strengths and areas of difficulty. Don't overlook your strong points; instead, devote more attention to enhancing your weaknesses. To review at the conclusion of each day, take notes every day.
9.How significant is consistent IPMAT revision?
Very crucial! Prior to the test, allot at least two weeks for revision. To become accustomed to the exam style and enhance your time, concentrate on completing practice questions and previous papers.
The IPMAT (Integrated Program in Management Aptitude Test) exam is primarily conducted for admission into five-year Integrated Program in Management (IPM) courses. Here are some key colleges that accept IPMAT scores:
1. **Indian Institute of Management (IIM) Indore**: IIM Indore was the first to introduce the IPM course, and it continues to use IPMAT scores for admission. Their program offers a strong foundation in management and business studies.
2. **Indian Institute of Management (IIM) Rohtak**: IIM Rohtak also accepts IPMAT scores for its IPM program, which focuses on grooming students for managerial and leadership roles through a mix of business and liberal arts education.
3. **Indian Institute of Management (IIM) Ranchi**: IIM Ranchi started its IPM program in 2021 and uses IPMAT scores for admission. This program aims to provide a multidisciplinary approach to management.
4. **Nirma University**: Nirma University’s Institute of Management in Ahmedabad accepts IPMAT scores for its Integrated BBA-MBA program, which combines undergraduate and graduate studies in management.
5. **TAPMI Bengaluru**: T.A. Pai Management Institute (TAPMI) in Bengaluru also considers IPMAT scores for its integrated program, though it is relatively new in the field.
Each of these institutions has its own admission process and eligibility criteria, so be sure to check specific requirements when applying.
In most Indian engineering colleges, if you choose to drop out after the first year, they often ask for fees for the entire program duration (all four years) before releasing your original documents. However, policies can vary between institutions, and some colleges might have different approaches. Here are some steps to handle this:
Check Your College Policy:
Look at the college’s official documents, like the student handbook, fee policy, or withdrawal policy. Some colleges might have a clause for students who want to transfer or drop out.
Visit the Administration or Academic Office:
Talk directly to the administration office about your plans. They can clarify the exact policy and let you know if you can retrieve your documents by paying only for the first year.
Negotiate with the College Authorities:
If possible, negotiate with the authorities, especially if you have a valid reason, like pursuing a different course. Sometimes, they may relax policies on a case-by-case basis.
Consider Legal Counsel:
If they are firm on charging fees for all four years and you feel it’s unfair, consulting with a lawyer can help. They can guide you on whether there’s a legal route to claim your documents without additional fees.
Also, it's great to see your commitment to join the IPMAT program for the IIM course! With careful planning, you can manage this transition smoothly.
To get into an IIM for a 5-year integrated program like IPM, you'll need to appear for the
IPMAT (Integrated Programme in Management Aptitude Test)
. CUET is not accepted for admission to IIMs.
IPMAT
is a specific entrance exam conducted by IIM Indore and IIM Rohtak for admission to their 5-year integrated management programs. It assesses your quantitative ability, verbal ability, and logical reasoning skills.
So, to get into an IIM for a 5-year program, focusing on preparing for the IPMAT exam is crucial.
It's crucial to take a methodical and focused approach to your IPMAT exam preparation in the last month. Understanding the IPMAT Indore exam format and syllabus should be your first priority if you haven't already begun studying for the test. The computer-based test mode will be used for the IPMAT Indore 2025. The IPMAT exam will take two hours to complete, and the question paper will consist of three sections. Examine the IPMAT's comprehensive curriculum and collect the necessary study materials, such as books, internet resources, sample papers, and past years' question papers, that address the key subjects of the test.
Online Bookstores:
Check platforms like Amazon, Flipkart, or other online bookstores for IPMAT preparation books. They often offer both physical and digital versions.
Educational Websites:
Websites like Careers360, Testbook, or Unacademy may offer e-books or study material for IPMAT. Visit their resources or study material sections.
Free Resources:
Some educational blogs or forums may share free e-books or study guides. Look for reliable sources or community groups dedicated to IPMAT preparation.
Libraries:
Check if your local or university library offers digital books or e-resources related to IPMAT.
Official IPMAT Websites:
Visit the official website for IPMAT or related educational institutes, as they may have recommended books or study materials.
For specific e-books, you can follow the link you mentioned or visit educational forums and websites for recommendations.
A career as Marketing Director is also known as a marketing expert who is responsible for the overall marketing aspect of the company. He or she oversees plans and develops the company's budget. The marketing Director collaborates with the business team to plan and develop the marketing and branding strategies for the company's products or services.
A Business Development Executive (BDE) is a professional responsible for identifying growth opportunities and fostering strategic partnerships to enhance a company's market position. Typically, a BDE conducts market research, analyses industry trends, and identifies potential clients or business prospects. He or she plays a crucial role in developing and implementing sales strategies to achieve revenue targets.
A BDE often collaborates with cross-functional teams, including marketing and product development, to align business objectives. Strong communication, negotiation, and relationship-building skills are essential for success in this role. BDE strives to expand the company's customer base, drive sales, and contribute to overall organisational growth in a dynamic and competitive business environment.
Content Marketing Specialists are also known as Content Specialists. They are responsible for crafting content, editing and developing it to meet the requirements of digital marketing campaigns. To ensure that the material created is consistent with the overall aims of a digital marketing campaign, content marketing specialists work closely with SEO and digital marketing professionals.
A sales manager is a revenue-generating source for a company. Any organisation or company which sells a commodity or service requires sales to generate revenue. A Sales manager is a professional responsible for supervising the sales team. An Individual as a sales manager works closely with salespeople, assigns sales territories, sets quotas, mentors the members of the sales, assigns sales training, and builds a sales plan.
The Sales Manager work also includes hiring and laying off sales personnel after evaluating his or her work performance. In bigger entities, sales quotas and plans are usually set at the executive level. He or she is responsible for overseeing the set target or quotas met by salespeople or upholding any policy. He or she guides his or her fellow salespeople and allows them to sell.
Individuals who opt for a career as a business analyst look at how a company operates. He or she conducts research and analyses data to improve his or her knowledge about the company. This is required so that an individual can suggest the company strategies for improving their operations and processes.
In a business analyst job role a lot of analysis is done, things are learned from past mistakes and the successful strategies are enhanced further. A business analyst goes through real-world data in order to provide the most feasible solutions to an organisation. Students can pursue Business Analytics to become Business Analysts.
A marketing manager is a person who oversees a company or product marketing. He or she can be in charge of multiple programmes or goods or can be in charge of one product. He or she is enthusiastic, organised, and very diligent in meeting financial constraints. He or she works with other team members to produce advertising campaigns and decides if a new product or service is marketable.
A Marketing manager plans and executes marketing initiatives to create demand for goods and services and increase consumer awareness of them. A marketing manager prevents unauthorised statements and informs the public that the business is doing everything to investigate and fix the line of products. Students can pursue an MBA in Marketing Management courses to become marketing managers.
An SEO Analyst is a web professional who is proficient in the implementation of SEO strategies to target more keywords to improve the reach of the content on search engines. He or she provides support to acquire the goals and success of the client’s campaigns.
Digital marketing is growing, diverse, and is covering a wide variety of career paths. Each job function aids in the development of effective digital marketing strategies and techniques. The aims and objectives of the individuals who opt for a career as a digital marketing executive are similar to those of a marketing professional: to build brand awareness, promote company services or products, and increase conversions. Individuals who opt for a career as Digital Marketing Executives, unlike traditional marketing companies, communicate effectively through suitable technology platforms.
